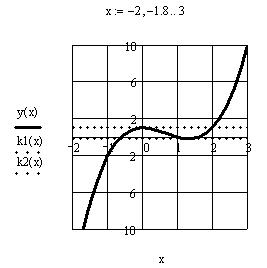
Определяем уравнения касательных. k1(x) := y(z0) + dy(z0) (x − z0).
k2(x) := y(z1) + dy(z1) (x − z1).
Строим график функций. Для вызова мастера построения графиков используем комбинацию клавиш «Shift+2». Для построения трех графиков в помеченном слева поле, через запятую вводим имена трех функций y(x), k1(x), k2(x). Устанавливаем диапазон изменения значения функций [–10, 10] и аргумента – [–2, 3], шаг между точками 0,2.
Пример 9. y = (arccos(x))2 . Найти y′′.
Решение: Вводим последовательность символов:
«Ctrl+Shift+/» (acos(x)^2П) Tab x Tab 2 simplify Enter.
|
|
1 |
|
|
d 2 |
(acos(x)2 ) simplify → 2 |
a cos(x) x −(1− x2 )2 |
. |
|
dx2 |
1 |
|||
|
|
|||
|
|
(1− x2 )2 (−1+ x2 ) |
|
Задание для самостоятельной работы.
Выполнить свой вариант типового задания по дифференцированию функции одной переменной из сборника типовых расче-
тов /4/.
4.4. Интегрирование функции одной переменной
Интегрирование в Mathcad реализовано в виде вычислительного оператора и устроено по принципу “как пишется, так и вводится“.
Для вызова операции вычисления неопределенного интеграла можно воспользоваться комбинацией клавиш «Ctrl+I», а для вызова определенного интеграла – «Shift+7».
4.4.1. Неопределенные интегралы
Рассмотрим несколько примеров интегрирования различных функций.
64
Пример 1. Найти интеграл ∫x4 4 1−3x5 dx .
Решение. Вводим последовательность символов: «Ctrl+I» x^4
П* «Ctrl+\» 1–3*x^5 Tab x Tab 4 «Ctrl+.» Enter. Напомним, что в данной последовательности П ─ символ пробела, Tab ─ символ
5
табуляции. ∫x4 4 1−3x5 dx → −754 (1−3 x5 )4 .
Полученную первообразную можно запомнить и построить ее график. Для этого включим режим оптимизации. Входим в пункт меню Tools и нажимаем на команду Optimization.
Вводя последовательность символов: F(x) «Shift+:» «Ctrl+I» x^4П* «Ctrl+\» 1–3*x^5 Tab x Tab 4 Enter, получаем пер-
вообразную в виде функции одной переменной.
F(x) := ∫x4 4 1−3x5 dx *.
Звездочка после первообразной показывает, что включен режим оптимизации.
Как известно, производная от первообразной равна подынтегральной функции. Проверим это для полученной первооб-
разной F(x). Вводим последовательность символов: «Shift+/» F(x) Tab x simplify Enter. Получаем:
1
dxd F(x) simplify → x4 (1−3 x5 )4 .
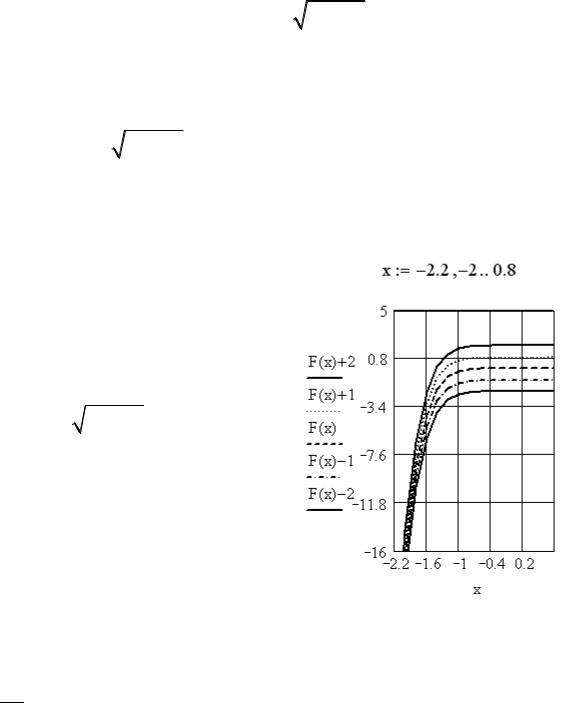
Теперь построим графики первообразных подынтегральной функции F(x)+C, при C= –2, C= –1, C=0, C=1 и C=2. Для этого вызываем мастер построения функций комбинацией клавиш «Shift+2». В помеченной слева позиции напишем через запятую все пять функций: F(x)+2, F(x)+1, F(x), F(x)–1, F(x)–2. В поле задания диапазона изменения аргумента вводим диапазон [–1.2, 0.8], а для диапазона значений функции выбираем отрезок [–16, 5].
65
Пример 2. Найти интеграл ∫7xx32+1dx .
Решение: Вводим последовательность символов: «Ctrl+I» x^2П/7*x^3П+1 Tab x «Ctrl+.» Enter. Получаем
∫ |
|
x2 |
|
1 |
|
ln(7 x3 +1). |
|
|
|
|
|
|
|
|
|
|||||
|
dx → |
|
|
|
|
|
|
|
|
|
|
|
||||||||
7x3 +1 |
21 |
|
|
x2 |
|
|
|
|
|
|
||||||||||
Пример 3. Найти интеграл ∫ |
|
|
|
|
|
|
dx . |
|
|
|||||||||||
(x2 + 4)(x + 2)(x −3) |
|
|
||||||||||||||||||
Решение. ∫ |
|
|
|
|
x2 |
|
|
|
dx → |
|
|
|
|
|
|
|||||
(x |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
+ 4)(x + 2)(x −3) |
|
|
|
|
|
|
|
|||||||
−1 |
|
|
|
9 |
|
|
1 |
ln(x2 |
|
|
5 |
|
x |
|
||||||
|
|
ln(x + 2) + |
|
|
|
ln(x −3) − |
|
|
+ 4) |
+ |
|
a tan |
|
. |
||||||
10 |
65 |
52 |
26 |
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Следует отметить, что далеко не все неопределенные интегралы так легко вычисляются. В некоторых случаях результат получается в достаточно сложном виде. Для того чтобы упростить результат, можно применить замену переменных в подынтегральном выражении. Учитывая, что при решении инженерных задач используются только определенные интегралы, в данном курсе пропустим методы замены в неопределенном интеграле.
4.4.2. Определенные интегралы
Определенный интеграл вычисляется в Mathcad численным методом, поэтому результат вычисления зависит от встроенной константы TOL, задающей точность всех приближенных вычислений. Напомним, что значение этой константы по умолчанию равно 0.001. Следует помнить, что при увеличении точности вычислений увеличивается и время расчета.
В Mathcad используются четыре численных метода интегрирования:
Romberg (Ромберга) – для гладких функций при ограниченных пределах интегрирования;
Adaptive (Адаптивный) – для быстроизменяющихся функций; Infinite Limit (Бесконечный предел) – для несобственных ин-
тегралов с бесконечными пределами интегрирования;
Singular Endpoint (Сингулярные) – модифицированный метод Ромберга, предназначенный для несобственных интегралов, с
66
особенностью на одном или обоих концах интервала интегрирования.
Чтобы задать метод интегрирования необходимо, вызвать контекстное меню свойств интеграла. Для этого необходимо, находясь на формуле интеграла, нажать правую кнопку мыши. В возникшем меню необходимо выбрать один из пяти пунктов предложенного контекстного меню: AtoSelect, Romberg, Adaptive, Infinite Limit или Singular Endpoint. При установке флажка AtoSelect (Автоматический выбор), Mathcad сам, в зависимости от подынтегральной функции и пределов интегрирования, выберет один из четырех методов и нарисует кружок перед названием выбранного метода.
При работе с определенными интегралами используют приближенное вычисление и символьное. Чтобы получить приближенный результат численным методом интегрирования, необходимо после ввода подынтегрального выражения ввести знак равенства. В этом случае Mathcad выводит полученное числовое значение с заданной при помощи параметра TOL точностью, если интеграл сходится, или символ ±∞, если интеграл несобственной и он расходится. При этом пределы интегрирования должны принимать только числовое значение, и подынтегральная функция обязана быть функцией одного аргумента, по которому производится интегрирование.
Приведем (без комментариев) несколько разнотипных примеров вычисления определенных интегралов численными методами:
1 |
|
|
|
|
|
|
1 |
|
∫x20dx = 0.048; |
∫t20dx = |
|||||||
0 |
|
|
|
|
|
|
0 |
|
∞ |
|
|
∞ |
|
π |
|||
1 |
|
1 |
dx = ; ∫4 |
|||||
∫ |
dx =1; |
∫ |
||||||
2 |
x |
|||||||
1 |
|
x |
1 |
0 |
||||
4 |
|
4 |
|
|
|
|
||
∫ |
|
|
dx |
= 0.928; |
||||
x2 +5 x +7 |
||||||||
0 |
|
|
|
|
|
|
|
|
1 1
; p := 0.5 ∫0 x p dx = 2;
tan(x) = 0.347;
1
∫e−x2 dx = 0.747.
0
∞ 1
−∞∫ 1+ x4 dx = 2.221.
При символьном вычислении необходимо использовать знак символьного равенства. Приведем те же примеры, что и при численном интегрировании:
67
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|||
∫x20dx → |
|
; |
|
|
|
∫t20dx →t20; |
|
p := 0.5 ∫ |
|
dx → 2; |
|
|
|
|
|
|||||||||||||||||||||||||||
21 |
|
|
|
|
|
p |
|
|
|
|
|
|||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
0 x |
|
|
|
|
|
|
|
|
|
|||||||
∞ |
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
|
|
|
|
|
|
|
1 |
dx → ∞; ∫4 tan(x) → |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
∫ |
dx →1; |
|
|
∫ |
|
ln(2); |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
1 |
|
x |
|
|
|
|
|
|
|
|
1 |
|
x |
|
|
1 |
|
0 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
∞ |
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∫ |
|
|
dx → |
|
π |
22. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
4 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
−∞1+ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
1 |
|
|
13 |
|
1 |
|
|
|
|
8 |
|
|
1 |
|
|
5 |
|
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
∫ |
|
|
|
|
|
|
|
|
|
dx → |
|
|
3 |
a tan |
|
|
|
3 |
− |
|
3 |
a tan |
|
3 |
||||||||||||||||||
x |
2 |
+5 x |
+7 |
3 |
|
|
3 |
|
|
|
3 |
|
|
3 |
|
. |
||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫e−x2 dx → |
|
erf (1) π 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
0 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
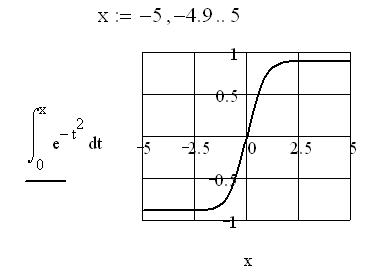
Определенные интегралы с переменными пределами интегрирования можно использовать как функции. В качестве примера
x
построим график функции f (x) = ∫e−t2 dt .
0
Задание для самостоятельной работы.
Выполнить свой вариант типового задания по интегралам из сборника типовых расчетов [4].
68