5.Решение обыкновенных дифференциальных уравнений

Обыкновенные дифференциальные уравнения представляют собой зависимость между искомой функцией одного аргумента, самим аргументом и производными искомой функцией различного порядка. При этом старшая степень производной, входящая в такую зависимость, называется порядком дифференциального уравнения. В работе [2] рассмотрены методы решения различных типов обыкновенных дифференциальных уравнений. Следует отметить, что во всех классических учебниках особое внимание уделяется аналитическим методам решения дифференциальных уравнений. При этом уже для уравнений первого порядка имеются только несколько типов уравнений, решаемых аналитически. При решении подавляющего большинства практических задач данные методы неприменимы вследствие сложности дифференциальных уравнений. Пакет Mathcad предназначен для решения практических задач, поэтому в него встроены численные методы решения задачи Коши и краевой задачи. Аналитическое решение дифференциальных задач при помощи пакета получить нельзя.

5.1.Решение задачи Коши

Вработе [2] рассмотрена постановка и решение задачи Коши методами Эйлера и Рунге–Кутта. В данной работе мы ограничимся программами расчета в рамках пакета Mathcad для решения задачи Коши дифференциального уравнения первого порядка, разрешенного относительно производной.

В качестве тестовой задачи выберем несложную задачу Коши, имеющую аналитическое решение.

Это легко интегрирующее уравнение с разделяющимися переменными. Общее решение получается следующим образом:

69

Начало программы.

Начальные данные.

Создание ранжированных векторов i и j , предназначенных для

организации циклов. i := 0..N j := 0..N −1

Вычисление координат узловых точек. xi = a + h i

Цикл последовательного вычисления значений искомой функции y(x) в узловых точках y1, y2 ,…, yN .

y0 := y0 y j+1 := y j + h f (x, y).

Вывод вектора решений.

yT = (1 1.1 1.248 1.48 1.879 2.665).

Конец программы.

Погрешность полученного решения накапливается на каждом интервале и принимает максимальное значение при x=1. Сравнивая полученное численное решение при N=5 с точным решением, получаем достаточно большую погрешность 4.434. При N=100 погрешность уменьшается до 0,991, а при N=1000 – до 0,123.

Осталось построить график полученного решения. Ниже мы приведем сравнительные графики решений для трех методов.

5.1.2. Решение задачи Коши методом Рунге–Кутта второго порядка

Метод Рунге–Кутта второго порядка точности описывается формулой, приведенной в работе [2].

Параметр α в данной формуле изменяется в диапазоне от 0 до 1 и задает скорость сходимости численного решения. Этот параметр необходимо подбирать для каждой конкретной задачи. Как показали численные исследования для задачи Коши (5.2) при ма-

71

В данном методе на каждой итерации правая часть вычисляется четыре раза в различных точках интервала [xi , xi+1].

Вычислительная программа имеет такой же вид, как и для метода Рунге–Кутта второго порядка.

Погрешность полученного решения при N=5 равна 0,242, при

N=100 – 0,000006 и при N=1000 – 6 10−10 . Таким образом, метод Рунге–Кутта четвертого порядка значительно точнее других методов при одинаковом уровне сложности алгоритмов.

Ниже на одной диаграмме представлены графики решений для всех трех методов при N=5 и график теоретического решения. Из графиков видно, что при переходе на следующий интервал ошибки накапливаются, при этом метод Рунге–Кутта четвертого порядка (yR4), уже при таком малом значении N, дает приемлемой результат. Метод Рунге–Кутта второго порядка (yR2) и метод Эйлера (yE) отслеживают тенденцию изменения теоретического решения, но дают большую погрешность.

73

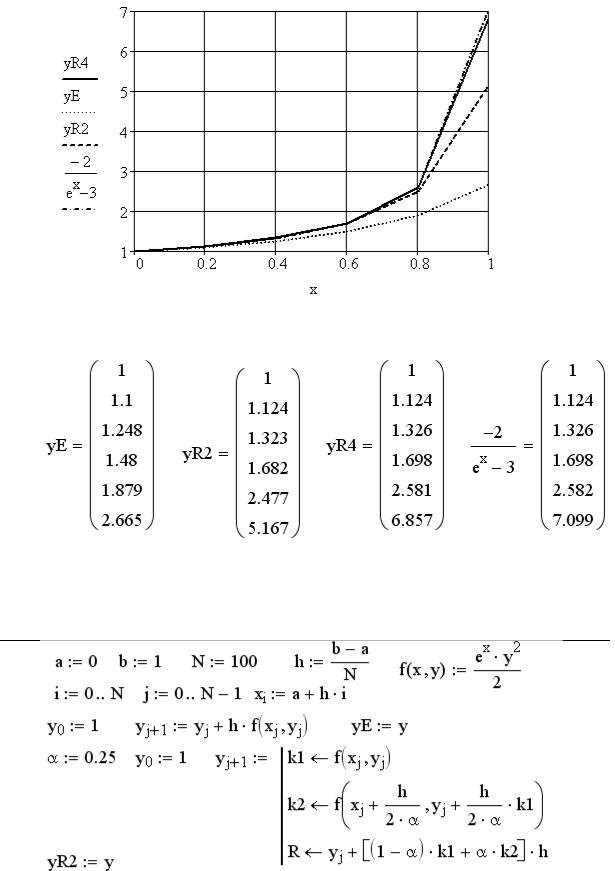
Здесь приведены значение всех трех методов и теоретического решения в узловых точках при N=5 и α = 0.5.

Для наглядности приведем полностью всю программу решения задачи Коши (5.2) всеми тремя методами при N=100.

Начало программы.

74

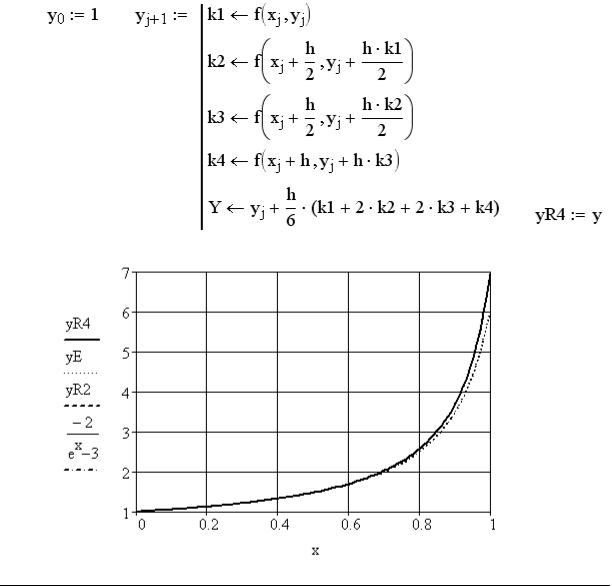
Конец программы.

Как видно из графиков, результаты, полученные по методу Рунге–Кутта второго и четвертого порядков, совпадают с теоретическим решением, а метод Эйлера требует увеличение числа N.

Задание для самостоятельной работы.

Решить задачу Коши (5.1) методом Эйлера и Рунге–Кутта второго и четвертого порядков точности для приведенных ниже уравнений и начальных данных. На одной диаграмме построить все три решения для трех значений параметра N: N=10, N=100 и

N=1000.

75