Задание для самостоятельной работы
Выполнить свой вариант типового задания по пределам функций числовых и последовательностей из сборника типовых расчетов [4].
4.2. Исследование сходимости и вычисление сумм рядов
Символьное вычисление конечных сумм и сходящихся чи-
словых рядов в Mathcad выполняется с помощью кнопки 
, находящейся в панели инструментов Calculas. Эту же операцию можно выполнить, нажав на комбинацию клавиш «Ctrl+Shift+4». Следует отметить, что не для всех сходящихся числовых рядов удается непосредственно найти суму ряда в символьном виде. В этом случае Mathcad выводит исходный ряд. Для дальнейшего исследования таких рядов необходимо исследовать при помощи признаков сходимости или находить частичные суммы таких рядов.
Решение примерного варианта
Рассмотрим методы вычисления сумм рядов на базе решения некоторых задач из примерного варианта №0 по теме ряды из работы [4].
Пример 1. Найти сумму ряда 12 + 232 + 253 + 274 +… Решение. Нетрудно заметить, что общий член данного ряда
= 2n −1
an − . Для вычисления суммы ряда вводим следующую по-
2n 1
следовательность нажатия клавиш: «Ctrl+Shift+4» (2*n–1)/2^n–1 Tab n Tab 1Tab «Ctrl+Shift+z» «Ctrl+.» Enter.
В результате получаем ∑∞ 2 n−−1 → 6.
n=1 2n 1
Ответ: Ряд сходится и сумма ряда равна 6.
54
∞ |
|
1 n |
|
Пример 2. Исследовать сходимость ряда ∑ 1 |
+ |
|
. |
|
|||
n=1 |
|
n |
|
Решение. Попробуем найти сумму ряда. Набираем последо-
вательность символов: «Ctrl+Shift+4» (1+1/nПП)^n Tab n Tab 1 Tab «Ctrl+Shift + z» «“Ctrl+.» Enter. В результате получаем
∞ |
|
|
1 |
n |
∞ |
|
|
1 |
n |
||
∑ |
1 |
+ |
|
|
→ ∑ |
1 |
+ |
|
. |
||
n |
n |
||||||||||
n=1 |
|
|
|
n=1 |
|
|
|||||
Это означает, что Mathcad не может найти сумму ряда или определить его расходимость. Необходимо провести более подробные исследования сходимости данного ряда.
Общий член ряда является функцией целочисленного аргу-
мента n |
a( n ) := |
1 + |
1 |
n . |
Найдем его предел lim a( n ) → exp(1). |
|
n |
||||||
|
|
|
|
n→∞ |
Следовательно, предел общего члена ряда равен числу e. Необходимое условие сходимости числового ряда не выполняется. Ряд расходится. Вводим функцию для суммы первых N слагаемых
N
исследуемого ряда S( N ) := ∑a( n ). Затем находим значение этой
n=1
функции для разных значений аргумента N. S(100) = 266.036;
S(1000 ) = 2.717 ×104 ; S(1000000 ) = 2.718 ×106 .
Мы видим, что с увеличением числа слагаемых сумма ряда пропорционально увеличивается. Следовательно, ряд расходится.
Ответ: Ряд расходится.
∞ |
1 |
|
|
Пример 3. Исследовать сходимость ряда ∑ |
. |
||
( n +1)! |
|||
n=1 |
|
Решение. Вводим последовательность символов:
«Ctrl+Shift+4» 1/(n+1)! Tab n Tab 1 Tab «Ctrl+Shift+z» simplify Enter. Кнопка simplify находится на панели инструментов Simbolic и предназначена для преобразования полученного результата к более простому выражению.
∞ |
1 |
|
|
|
В результате получаем ∑ |
|
simplify → exp(1) −2. |
||
(n +1)! |
||||
n=1 |
|
|||
Ответ: Ряд сходится и сумма ряда равна e –2.
55
∞ |
n |
n |
||
Пример 4. Найти сумму ряда ∑ |
|
|
. |
|
2n +1 |
||||
n=1 |
|
|||
Решение. Попытаемся вычислить сумму этого ряда в символьном виде. Вводим последовательность символов: «Ctrl+ Shift+4» (n/1*n+1ПП)^n Tab n Tab 1 Tab «Ctrl+Shift+z» «Ctrl+.» Enter. Получаем такой же ответ, как и условие. Это означает, что Mathcad не может получить сумму этого ряда в символьном виде. Проводим дополнительные исследования. Вводим функцию целочисленного аргумента n, совпадающую с общим членом данно-
го ряда. |
a( n ) := |
n |
|
n |
. Проверяем необходимый признак |
|
2 n +1 |
||||||
|
|
|
|
|||
сходимости ряда. Для этого находим предел общего члена ряда.
lim a( n ) →0. Следовательно, необходимый признак сходимости
n→∞
ряда выполняется, ряд может сходиться. Проверяем, выполняется ли достаточный признак сходимости. Применяем признак Далам-
бера. lim |
a( n +1) |
|
→ |
1 |
. Предел меньше 1, поэтому ряд сходится. |
|||
|
2 |
|||||||
n→∞ |
a( n ) |
|
|
|
|
|||
Рассмотрим |
последовательность |
частичных |
сумм: |
|||||
n |
|
|
|
|
|
|
|
|
S( n ) := ∑a( k ). |
|
|
|
|
|
|||
k=1
Построим график этой целочисленной функции. Из графика видно, что последовательность достаточно быстро сходится к некоторому числу. Найдем значения функции S(n) в некоторых точках. S(51)= 0.6497624; S(52)=0.65. Найдем
значение частичной суммы при достаточно большом значении n. S(100000)=0.65. Следует отметить, что вычисление последней суммы занимает значительное время.
Ответ: S=0,65.
Пример 5. Найти сумму ряда ∑∞ ( −1)n +1.
n=1 n!
56
Решение. Попытаемся найти сумму ряда, вводя последова-
тельность символов: «Ctrl+Shift+4» ((–1)^nП+1ППn! Tab n Tab 1 Tab «Ctrl+Shift+z» “Ctrl+.” Enter. Получаем
∞ |
(−1) |
n |
+1 |
∞ |
(−1) |
n |
+1. Это означает, что Mathcad не может |
∑ |
|
→ ∑ |
|
||||
n=1 |
n! |
|
n=1 |
n! |
|
||
|
|
|
|
|
|
||
решить данную задачу, необходимы более глубокие исследования.
Рассмотрим последовательность частичных сумм
S( n ) = ∑n (−1)k +1 .
k =1 k !
Построим график целочисленной функции S(n). Из графика видно, что последовательность быстро сходится к некоторому числу S, равному сумме ряда. Находим значение последовательности S(n) в некоторых точках.
S(5)=1.08333333; S(10)=1.08616127;
S(20)=1.08616127. Ответ: S=1,08616127.
∞ |
n |
+1) |
|
Пример 6. Найти сумму ряда ∑ |
( −1 ) ( 2n |
. |
|
|
|
||
n=1 |
n( n +1 ) |
||
|
|
|
|
Решение. С помощью клавиатуры набираем команду:
«Ctrl+Shift+4» (–1)^nП(2*n+1)П/n*(n+1) Tab n Tab 1 Tab «Ctrl+Shift+z» Ctrl+. Enter. В результате получаем:
∞ |
( −1 )n( 2n +1 ) |
→ −1. |
∑ |
|
|
n( n +1 ) |
||
n=1 |
Ряд сходится, сумма ряда равна 1. Для исследования ряда на |
|
|
||
абсолютную сходимость при помощи мыши переходим в поле
формулы и убираем множитель( −1)n . Получаем ∞∑ ( 2n +1 ) → ∞.
n=1 n( n +1 )
Ответ: Ряд сходится условно, сумма ряда равна –1. Пример 7. Найти интервал сходимости степенного ряда и на
найденном интервале построить график функции S( x ) = |
∞ |
xn |
|
∑ |
|
. |
|
|
|||
|
n=1 n! |
||
57
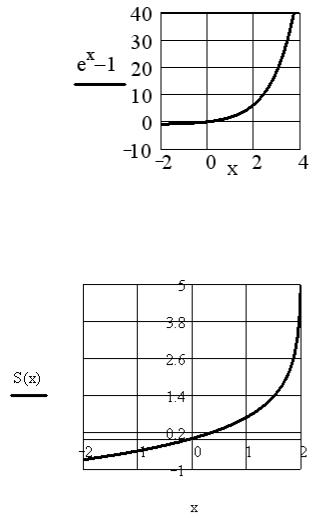
Решение. Исследуем сходимость ряда по признаку Даламбе-
ра. a( n,x ) := |
xn |
|
a( n +1,x ) |
→ 0. |
|
|
; |
lim |
|
||
|
a( n,x ) |
||||
|
n! |
n→∞ |
|
||
Таким образом, предел равен нулю для любого значения x. Следовательно, ряд сходится на всей числовой оси. Попытаемся найти сумму ряда.
∞ |
xn |
|
∑ |
|
→ exp( x ) ( 1 − exp( −x )). |
|
||
n=1 n! |
||
Упрощая полученный Mathcad
результат, получаем S(x)=ex–1. Строим график полученной функции.
Ответ: Ряд сходится при x R , сумма ряда равна ex–1. Пример 8. Найти инте-
рвал |
сходимости степенного |
|||||||||||||
ряда |
|
и |
построить |
график |
||||||||||
функции |
|
|
|
S(x) = |
∞ |
xn |
|
. |
||||||
|
|
|
∑ |
|
|
|||||||||
|
|
|
|
n |
||||||||||
Решение. |
|
|
|
|
|
|
n=1 n 2 |
|
|
|||||
Общий член ряда |
||||||||||||||
a(n) := |
|
xn |
; |
|
|
|
|
|
|
|
||||
|
n 2n |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
lim |
a(n +1, x) |
|
→ |
1 |
x. |
|
|
|
|
|||||
|
|
|
|
|
|
|||||||||
n→∞ |
a(n, x) |
|
|
2 |
|
|
|
|
|
|||||
Следовательно, согласно признаку Даламбера, ряд сходится при
| x | |
<1, |
т.е. при x (–2; 2). |
При x= –2, ряд сходится условно |
|||||||||||
|
2 |
|
||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|||
|
∞ |
|
|
|
|
|
|
|
|
|
|
|||
∑(−n1) |
→ −ln(2). Вычислим сумму ряда |
|||||||||||||
n=1 |
|
|
|
xn |
|
|
|
|
|
|
|
|||
S(x) := |
∞ |
|
|
|
→ −ln(1− |
1 |
x) |
и построим график функции S(x). |
||||||
∑ |
|
|
|
|
|
|
|
|||||||
|
|
|
n |
2 |
||||||||||
|
|
|
|
= |
|
2 |
|
|
|
|||||
|
|
|
n 1 n |
|
|
|
|
|
|
|
|
|||
|
|
|
Ответ: Ряд сходится на отрезке x [ −2;2 ] и сумма ряда |
|||||||||||
равна −ln(1− |
|
1 |
x) . |
|
|
|
||||||||
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
58
Пример 9. Разложить функцию f ( x ) = |
x −2 |
в ряд Тей- |
|
||
x2 + 4x +8 |
||
лора по степеням (x+2).
Решение: В Mathcad есть команда “разложить функцию в ряд Маклорена по степеням x”. Сделаем замену переменных t=x+2 или x=t–2. Для этого активизируем панель инструментов Symbolic. Напомним, как это сделать. Последовательно входим в меню View/Toolbars/Symbolic. Вводим правую часть функции f(x). Нажимаем левой клавишей на кнопку substitute из панели Symbolic. В первой помеченной позиции вводим имя переменной x, а во второй выражение t–2. Чтобы упростить полученное выражение, нажимаем кнопку simplify. В результате получаем
|
|
x −2 |
substitute, x = t −2 → |
t −4 |
|
simplify → |
t |
−4 |
. |
|||
x |
2 |
+ 4 |
x +8 |
2 |
+ 4 |
t |
t |
2 |
+ 4 |
|||
|
|
( t −2 ) |
|
|
|
|||||||
Копируем полученную функцию и нажимаем на кнопку series. В первой помеченной позиции вводим имя переменной t, по которой необходимо разложить функцию в ряд Тэйлора, а во вторую – количество членов разложения – 6. Получаем первые
шесть членов в разложении функции |
|
t −4 |
|
в ряд Маклорена по |
||||||||||||||||||||||
|
t2 + 4 |
|||||||||||||||||||||||||
степеням t: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
t |
−4 |
series,t,6 |
→ −1+ |
1 |
t + |
1 |
t |
2 |
− |
|
1 |
t |
3 |
− |
|
1 |
t |
4 |
+ |
1 |
t |
5 |
. |
||
|
t2 |
+ 4 |
4 |
4 |
|
16 |
|
16 |
|
64 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
В полученном разложение нетрудно найти закономерность изменения слагаемых и функцию tt2 −+44 , записать в виде степен-
ного ряда:−1+ ∑∞ (−1)n+1 (t2n−1 +t2n ).
n=1 4n
Производя обратную подстановку t=x+2, получаем ответ:
−1+ ∑∞ (−1)n+1 ((x + 2)2n−1 +(x + 2)2n ).
n=1 4n
Проверим полученный результат. Для этого, находясь внутри предыдущей формулы, подаем команду вычислить сумму ряда, вводя комбинацию клавиш: «Ctrl+.» Enter. Для упрощения полу-
59
ченного результата нажимаем клавишу simplify и получаем первоначальную функцию:
1 |
1 |
1 |
|
2 |
|
|
|
|
|
||
−1+ |
4 |
x + 2 + |
4 (x + 2) |
simplify → |
|
x −2 |
. |
|
|||
|
1 |
|
|
x2 |
|
|
|||||
|
|
|
2 |
+ x |
|
|
+ 4x +8 |
|
|||
|
|
2 + 4 x |
|
|
|
|
1 |
|
|
||
Пример 10. Разложить функцию |
|
в ряд Маклорена. |
|||||||||
x2 −3x + 2 |
|||||||||||
Решение. Вводим функцию и нажимаем на кнопку series из панели инструментов Symbolic. В помеченных позициях вводим x и 7. В результате получаем первые семь членов в разложении функции в ряд Маклорена:
|
1 |
series, x,7 |
→ |
1 |
+ |
3 |
x + |
7 |
x |
2 |
+ |
15 |
x |
3 |
+ |
31 |
x |
4 |
+ |
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x2 |
−3 x + 2 |
2 |
4 |
8 |
|
16 |
|
32 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
+6463 x5 +127128 x6.
Вкраткой форме этот ряд можно записать в виде:
∞ |
|
|
|
1 |
|
|
|
|
|
|
∑ |
1 |
− |
|
|
|
xn. |
|
|
|
|
2 |
n |
|
|
|
||||||
n=0 |
|
|
|
|
|
|
|
|
|
|
Для проверки результата подаем команду “вычислить сумму |
||||||||||
ряда в символьном виде”: «Ctrl+.» Enter. |
||||||||||
∞ |
|
|
|
1 |
|
|
|
1 |
|
|
∑ |
1 |
− |
|
|
|
|
xn → |
|
|
. |
|
|
|
(x −1) |
(x −2) |
||||||
n=0 |
|
|
|
2n |
|
|
||||
Пример 11. Вычислить 5 35 с точностью до 0,0001. Решение. Установим режим вывода результатов с точностью
четыре знака после запятой. Для этого заходим в подменю Result…, входящее в главное меню Format. В открывшемся диа-
логовом окне в поле Number of decimal places закладки Number Format устанавливаем значение 4. В этом случае все расчеты производятся с четырьмя знаками после запятой. Дальше активизируем панель инструментов Calculator. Мышкой нажимаем на
кнопку n . Это же можно сделать без использования панели инструментов Calculator, применяя “горячую” клавишу «Ctrl+\». Далее вводим подкоренное выражение, нажимаем клавишу Tab и
вводим степень корня. Получаем ответ: 5 35 = 2.0362.
60