
- •Математический практикум с применением пакета Mathcad
- •Оглавление
- •1. Введение в Mathcad
- •1.1. Интерфейс Mathcad
- •1.1.1. Главное меню Mathcad
- •1.1.2. Панели инструментов
- •2. Задачи элементарной математики
- •2.2. Построение графиков функций
- •2.3. Решение алгебраических уравнений и систем
- •3. Задачи линейной алгебры
- •3.1. Основные сведения о матричных операциях
- •3.2. Решение типовых задач по линейной алгебре
- •4. Задачи математического анализа
- •4.1. Вычисление пределов числовых последовательностей и функций
- •4.2. Исследование сходимости и вычисление сумм рядов
- •4.3. Дифференцирование функций одной переменной
- •4.4. Интегрирование функции одной переменной
- •4.4.1. Неопределенные интегралы
- •4.4.2. Определенные интегралы
- •5.1. Решение задачи Коши
- •5.1.1. Решение задачи Коши методом Эйлера
- •5.1.2. Решение задачи Коши методом Рунге–Кутта второго порядка
- •5.1.3. Решение задачи Коши методом Рунге–Кутта четвертого порядка
- •5.1.4. Решение задачи Коши при помощи встроенных функций
- •5.2. Решение краевой задачи
- •6. Теории вероятностей и математическая статистика
- •6.1. Дискретные случайные величины
- •6.2. Непрерывная случайная величина
- •7. Программирование в Mathcad
- •Заключение
- •Предметный указатель
- •Список литературы

6. Теории вероятностей и математическая статистика
С появлением мощных персональных компьютеров и математических пакетов возникла необходимость в перестроении методики преподавания теории вероятности и особенно математической статистики. Появилась возможность освободить человека от рутинной работы по обработке большого объема статистической информации и поручить эту работу вычислительной программе. Рассмотрим некоторые возможности Mathcad при работе с задачами теории вероятностей и математической статистики.
При решении задач теории вероятностей часто необходимо использовать достаточно трудоемкие функции комбинаторики. Рассмотрим вычисление таких функций в рамках пакета Mathcad.
Число перестановок Pn = n!. В Mathcad эта функция записы-
вается так же как в математике и вычисляется в диапазоне от 0 до
170. Например: 0! =1; 4! = 24; 10! = 3.629×106 ; 100! = 9.333×10157 ;
170! = 7.257 ×10306 ; |
10! |
|
= 45. |
|||||
8! 2! |
||||||||
|
|
|
|
|
|
|||
Число |
сочетаний |
из n элементов по k элементов |
||||||
Ck = |
n! |
|
|
вычисляется при помощи функции combin(n, k). |
||||
|
|
|
||||||
n |
k!(n −k)! |
|
|
|
|
|||
|
|
|
|
|
||||
Пример. Найти вероятность того, что при случайном выборе 10 шаров из урны, содержащей 20 шаров, из которых 6 белых и 14 черных, среди выбранных окажется 4 белых и 6 черных.
Решение данной задачи можно записать в виде
C4 C6
P(A) = 6 14 . Программа, решающая поставленную задачу,
C2010
имеет вид
P := |
combin(6,4) combin(14,6) |
P = 0.244. |
|
combin(20,10) |
|||
|
|
93

Число размещений из n элементов по k элементов вычисляется по формуле Ank = (n −n!k)!. Для вычисления числа размеще-
ний в Mathcad встроена функция permut(n, k).
6.1. Дискретные случайные величины
Понятие случайной величины является основным в теории вероятностей и ее приложениях. Напомним, что случайной величиной называется переменная величина, которая в результате опыта может принимать то или иное, заранее неизвестное, числовое значение.
Рассмотрим вначале дискретную случайную величину, воз-
можные значения которой образуют конечную последовательность {xi }, состоящую из n действительных чисел с некоторыми
известными вероятностями {pi }. Обычно такую последовательность упорядочивают по возрастанию значений xi . Таким образом, дискретная случайная величина ξ , принимающая значения
x1 < x2 < x3 < < xn с вероятностями p1, p2 , p3 , , pn , может быть задана законом распределения и может быть представлена таблицей:
ξ |
x1 |
x2 |
x3 |
|
xn |
р |
p1 |
p2 |
p3 |
|
pn |
Данную таблицу в Mathcad можно хранить в виде матрицы P, состоящей из двух строк и n столбцов или в виде двух векторов X и P, что чаще бывает удобнее. Поскольку в каждом из испытаний случайная величина принимает всегда какое-либо значение из области ее изменения, должно выполняться следующее условие
n
∑pi =1.
i=1
Функция распределения дискретной случайной величины F(x) = P(ξ < x) имеет вид:
94

0, |
|
|
x < x1, |
|
|||
p , |
|
x |
≤ x < x , |
||||
|
1 |
+ p , |
1 |
≤ x |
2 |
||
p |
x |
< x , |
|||||
F(x) = |
1 |
2 |
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
p |
+ p |
+ + p , |
x |
|
≤ x < x , |
||
|
1 |
2 |
n |
n−1 |
|
n |
|
1, |
|
|
|
x > xn . |
|||
Математическим ожиданием M (ξ)
(6.1)
дискретной случайной
величины ξ называется сумма произведений всех ее значений на соответствующие вероятности:
n |
|
M (ξ) = ∑xi pi . |
(6.2) |
i=1
Дисперсией случайной величины ξ называется математиче-
ское ожидание квадрата ее отклонения от математического ожидания:
D(ξ) = M (ξ − M (ξ))2 . |
(6.3) |
Часто для вычисления дисперсии удобнее применять следующую формулу:
D(ξ) = M (ξ2 ) −(M (ξ))2 . |
(6.4) |
Средним квадратическим отклонением случайной величины ξ называется квадратный корень из ее дисперсии:
σ(ξ) = D(ξ) . |
(6.4) |
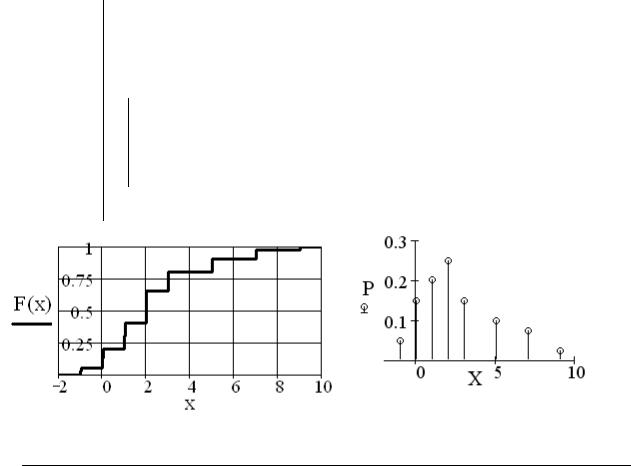
Пример. Случайная величина ξ задана следующим законом распределения:
ξ |
–1 |
0 |
1 |
2 |
3 |
5 |
7 |
9 |
P |
0,05 |
0,15 |
0,2 |
x |
0,15 |
0,1 |
0,075 |
0,025 |
Найти неизвестную величину x и построить график функции распределения для дискретной величины ξ , построить много-
угольник распределения этой величины. Найти математическое ожидание, дисперсию и среднеквадратическое отклонение дискретной величины ξ .
Напишем универсальную программу для решения данной задачи в рамках пакета Mathcad. Заданную таблицу введем в двумерный массив A, состоящий из двух строк и N столбцов. Неиз-
95

n
вестную величину x определяем из условия ∑Pi =1. В одномер-
k=1
ные массивы X и P введем первую и вторую строки матрицы A. Для определения значения функции распределения в программе используется оператор цикла while. В операторе цикла мы накапливаем сумму вероятностей Pi до тех пор, пока аргумент функ-
ции x больше чем Xi , при этом увеличивая на 1 индекс i. После
определения функции F(x) мы строим графики функции распре-
деления F(x) и график многоугольника распределения, т.е. зави-
симость P от X. При построении графика многоугольника распределения необходимо отформатировать тип линии, задав параметр TYPE равным stem. Написанная программа является универсальной, и для решения другой аналогичной задачи необходимо ввести новое значение N и новую матрицу A.
Начало программы.
|
|
|
|
|
|
|
|
|
|
|
ORIGIN :=1 |
n :=8 |
a := 0 |
|
|
|
|
||
|
Закон распределения. |
|
5 7 |
9 |
|
||||
|
−1 |
0 |
1 |
2 3 |
|
||||
|
A := |
0.15 0.2 |
|
a 0.15 0.1 0.075 0.025 |
|
||||
|
0.05 |
|
|
||||||
|
Найдем неизвестную величину a. |
|
|
|
|||||
|
n |
|
|
|
|
|
|
|
|
|
a :=1−∑A2,k |
A2,4 := a |
|
|
|
|
|||
|
k=1 |
|
|
|
|
|
|
|
|
|
X := (AT )1 |
|
P := (AT ) 2 |
|
|
|
|
||
Найдем математическое ожидание случайной величины ξ .
n
M := ∑Pi Xi M = 2.35
i=1
Дисперсию найдем двумя способами по формулам (6.3) и (6.4).
n |
− M )2 Pi D = 5.278. |
|
|
D := ∑(Xi |
|
||
i=1 |
|
|
|
n |
(Xi )2 |
|
|
M 2 := ∑Pi |
D := M 2 − M 2 |
D = 5.278. |
|
i=1
σ := D σ = 2.297
Функция распределения F(x).
96
F (x) := s ← 0 i ←1
while x > Xi s ← s + Pi i ←i +1
break if i > n
s
Конец программы.
В математике принято изображать функцию распределения для дискретной случайной величины в виде кусочно-постоянной функции со стрелочками влево. К сожалению, такая возможность в Mathcad не предусмотрена.
Задание для самостоятельной работы.
Дискретная случайная величина ξ принимает 9 следующих
значений: –2; 0; 1; 2; 4; 5; 7; 8; 10. Массив вероятностей для 30 различных вариантов, соответствующий данным значениям случайной величины ξ , представлен в таблице. Вместо величины
x поставить недостающее число. Для указанного преподавателем варианта построить график функции распределения для дискретной величины ξ и график многоугольника распределения. Найти
вероятность того, что значение дискретной случайной ξ величи-
ны заключено в диапазоне от 0 до 4. Найти математическое ожидание, дисперсию и среднеквадратическое отклонение заданной случайной величины.
№ |
|
|
Значение массива вероятностей |
|
|
||||
Вар. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
97
1 |
0,02 |
0,01 |
0,05 |
0,1 |
0,15 |
x |
0,25 |
0,15 |
0,1 |
2 |
0,02 |
0,03 |
0,02 |
0,06 |
0,3 |
x |
0,13 |
0,05 |
0,1 |
3 |
0,02 |
0,05 |
x |
0,11 |
0,14 |
0,071 |
0,15 |
0,07 |
0,2 |
4 |
0,05 |
0,4 |
0,01 |
0,13 |
0,06 |
0,06 |
0,02 |
x |
0,06 |
5 |
0,04 |
0,23 |
0,03 |
0,03 |
0,15 |
x |
0,24 |
0,11 |
0,06 |
6 |
0,03 |
0,04 |
0,02 |
0,04 |
0,2 |
0,25 |
0,07 |
0,1 |
x |
7 |
0,3 |
0,12 |
x |
0,32 |
0,01 |
0,02 |
0,07 |
0,01 |
0,05 |
8 |
0,05 |
0,1 |
0,23 |
0,04 |
x |
0,05 |
0,1 |
0,23 |
0,04 |
9 |
0,2 |
0,1 |
0,14 |
0,06 |
0,05 |
0,3 |
0,01 |
0,01 |
x |
10 |
0,01 |
0,05 |
0,2 |
0,03 |
0,04 |
0,01 |
0,2 |
0,32 |
x |
11 |
0,4 |
0,02 |
0,09 |
0,06 |
0,3 |
0,05 |
0,03 |
0,02 |
x |
12 |
0,05 |
0,2 |
0,5 |
0,03 |
0,01 |
0,01 |
0,05 |
0,04 |
x |
13 |
0,01 |
0,04 |
0,2 |
0,25 |
0,05 |
0,06 |
0,02 |
0,06 |
x |
14 |
0,2 |
0,1 |
0,05 |
0,06 |
0,07 |
0,06 |
0,1 |
0,3 |
x |
15 |
0,08 |
0,02 |
0,1 |
0,3 |
0,1 |
0,049 |
0,08 |
0,14 |
x |
16 |
0,06 |
0,2 |
0,34 |
0,07 |
0,05 |
0,06 |
0,02 |
0,1 |
x |
17 |
0,5 |
0,05 |
0,07 |
0,03 |
0,09 |
0,1 |
0,03 |
0,02 |
x |
18 |
0,03 |
0,03 |
0,02 |
0,5 |
0,2 |
0,02 |
0,05 |
0,03 |
x |
19 |
0,02 |
0,06 |
0,3 |
0,07 |
0,01 |
0,3 |
0,01 |
0,03 |
x |
20 |
0,05 |
0,4 |
0,05 |
0,02 |
0,05 |
0,01 |
0,02 |
0,3 |
x |
21 |
0,01 |
0,2 |
0,5 |
0,02 |
0,05 |
0,056 |
0,06 |
0,01 |
x |
22 |
0,6 |
0,02 |
0,05 |
0,1 |
0,05 |
0,03 |
0,04 |
0,01 |
x |
23 |
0,2 |
0,04 |
0,05 |
0,06 |
0,4 |
0,1 |
0,05 |
0,04 |
x |
24 |
0,06 |
0,02 |
0,03 |
0,2 |
0,06 |
0,2 |
0,06 |
0,1 |
x |
25 |
0,1 |
0,23 |
0,04 |
0,05 |
x |
0,03 |
0,05 |
0,1 |
0,2 |
26 |
0,02 |
0,2 |
0,5 |
0,02 |
0,1 |
0,05 |
0,02 |
0,04 |
x |
27 |
0,07 |
0,02 |
0,07 |
0,2 |
0,5 |
0,02 |
0,05 |
0,01 |
x |
28 |
0,05 |
0,4 |
0,01 |
0,05 |
0,11 |
0,088 |
0,04 |
0,1 |
x |
29 |
0,4 |
0,05 |
0,06 |
0,02 |
0,2 |
0,05 |
0,02 |
0,1 |
x |
30 |
0,05 |
0,05 |
0,05 |
0,05 |
0,05 |
x |
0,1 |
0,23 |
0,04 |
Рассмотрим наиболее распространенные распределения дискретной случайной величины, используемые при решении практических задач теории вероятностей. К таким распределениям можно отнести: биномиальное, геометрическое и пуассоновское распределения.
98

Биномиальное распределение (распределение Бернулли).
Пусть проводится серия из n повторных испытаний, в каждом из которых вероятность наступления некоторого события A постоянна и равна p, а вероятность не наступления этого события рав-
на q. При этом q = P(A) =1− p. Можно ввести случайную величину ξ , равную числу наступления события A в серии из n испытаний. Эта случайная величина является дискретной и принимает значения от 0 до n с разными значениями вероятностей. Распределение такой случайной величины называется биномиальным и задается формулой повторных испытаний Бернулли
P (k) = P(ξ = k) = Ck pk qn−k , |
(6.6) |
|||
n |
n! |
|
n |
|
где k = 0,1,2, ,n, Cnk = |
. |
|
||
k!(n −k)! |
|
|||
|
|
|
||
Для нахождения распределения вероятностей биномиального закона в Mathcad встроена функция dbinom(k, n, p), а для определения функции распределения – функция pbinom(k, n, p).
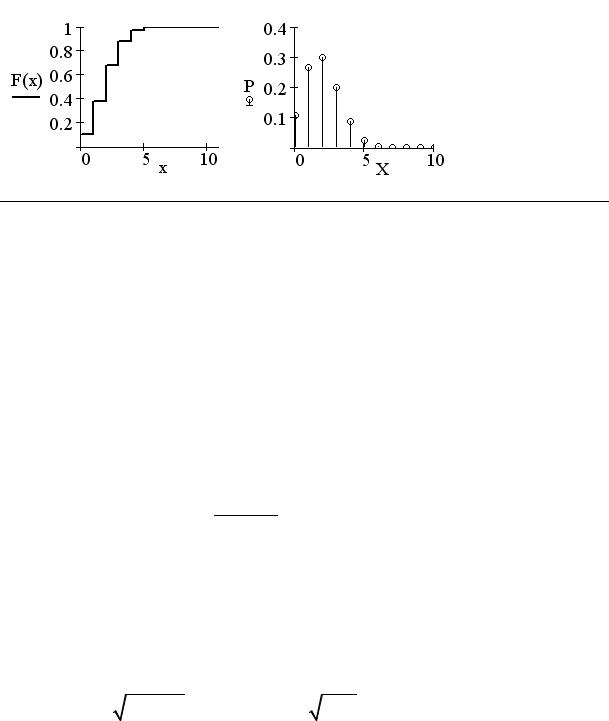
Пример. Производится 10 одинаковых опытов. В каждом опыте вероятность появления события A постоянна и равна 0,2. Построить график функции распределения и многоугольник распределения. Найти вероятность того, что число опытов, в которых появится событие A, будет не менее 5. Найти наивероятнейшее число появления события A.
Напишем программу на Mathcad, решающую поставленную задачу.
Начало программы.
|
|
|
|
|
|
n :=10 |
p := 0.2 |
|
k := 0..n |
|
|
Xk := k |
Pk := dbinom(k,n, p) |
∑P =1 |
|
||
max(P) = 0.302 |
min(P) =1.024×10−7 |
|
|||
|
|
|
|
|
n |
F(x) = pbinom(x,n, p) |
F(n) − F(4) = 0.033 |
∑Pk = 0.033 |
|||
k=5
99
Конец программы.
Для определения искомой вероятности в программе исполь-
n
зуются два метода: F(n) − F(4) = 0.033 и ∑Pk = 0.033. Из гра-
k=5
фика многоугольника распределения видно, что наивероятнейшее
число появления события A равно значениюk* = 2 .
При больших значениях n подсчет вероятности по формуле Бернулли связан с громоздкими вычислениями. При этом необходимо применять методы, которые уменьшают ошибки округления при делении и умножении сверхбольших чисел. Следует
отметить, что число 100! ≈10158 и для его вычисления необходимо выполнить 99 операций умножения. Для того чтобы вычислить, например C10040 = 40!100!60!, необходимо написать программу,
которая производит сокращение числителя и знаменателя, а только затем производила бы умножение и деление, с учетом увеличения точности результата. До появления пакетов программ, аналогичных пакету Mathcad, применялась приближенная формула, соответствующая локальной теореме Лапласа:
P (k) ≈ |
1 |
e−0,5x2 , x = |
k −np |
. |
(6.7) |
|
|
||||
n |
2πnpq |
|
npq |
|
|
|
|
|
|||
Функцию dbinom можно применять и при больших значениях числа испытаний. Рассмотрим процесс сходимости формулы Бернулли (6.6) к локальной теореме Лапласа (6.7). Для этого рассмотрим повторные испытания, в которых вероятность события A равна p=0,1, а в качестве k выберем наивероятнейшее число равное np . Функция round используется (в приведенной ниже
программе) для округления числа до целого значения.
100

Напишем подпрограмму dLapl(k, n, p), реализующую локальную формулу Лапласа.
Начало программы.
|
|
|
|
|
|
|
n :=1000000 p := 0.1 |
k = round(n p) k =100000 |
|||||
dLapl(k,n, p) := |
|
q ←1− p |
||||
|
||||||
|
|
|
y ← |
|
1 |
|
|
|
|
|
n p q |
||
|
|
|
y |
e−0.5 [(k −n p) y]2 |
||
|
|
|
2 π |
|||
|
|
|
|
|
||
Выводим значения, полученные по формуле Бернулли и локальной теореме Лапласа, а также модуль разности этих значений. dbinom(k,n, p) = 0.00132981 dLapl(k,n, p) = 0.00132981
| dbinom(k,n, p) −dLapl(k,n, p) |=1.12282×10−9
Конец программы.
В результате при n=1000000 и к=100000, по обоим методам мы получили почти одинаковые результаты. По представленной выше программе легко заполнить таблицу сходимости решений по двум сравниваемым формулам.
N |
5 |
10 |
20 |
50 |
100 |
1000 |
M |
1 |
1 |
2 |
5 |
10 |
100 |
Pn (m) |
0.328 |
0.387 |
0.2851 |
0.18849 |
0.13187 |
0.04202 |
Ln (m) |
0.450 |
0.42 |
0.2974 |
0.18806 |
0.13298 |
0.04205 |
| Pn (m) − Ln (m) | |
0.122 |
0.033 |
0.0122 |
0.00314 |
0.00112 |
0.00003 |
Мы видим, что при n=20 погрешность локальной теоремы Лапласа составляет около 0,01. Кроме того, из приведенных исследований можно сделать вывод, что на современном этапе развития компьютерных технологий формулу Бернулли можно применять для любых значений параметров n и m.
В случае, если необходимо найти вероятность того, что случайная величина ξ удовлетворяет неравенству k1 ≤ξ ≤ k2 , при
больших значениях числа повторных испытаний применяется интегральная теорема Лапласа:
P |
(k |
≤ξ ≤ k |
2 |
) ≈ |
1 |
x2 e−0,5t2 dt, |
x = |
ki −np |
, i =1,2. |
(6.8) |
|
|
|||||||||
n |
1 |
|
|
2π x∫ |
i |
npq |
|
|
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
|
|
||
101

Эту теорему можно записать в виде
P |
(k ≤ξ ≤ k |
|
) ≈φ |
|
k2 −np |
|
|
−φ |
|
k1 |
−np |
, |
(6.9) |
|||
2 |
|
|
|
|
|
|||||||||||
n |
1 |
|
|
|
|
npq |
|
|
|
|
|
|||||
|
|
|
|
|
x |
|
|
|
|
npq |
|
|
||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
где φ(x) = |
|
∫ e−0,5t2 dt |
|
– функция Лапласа. Для вычисле- |
||||||||||||
|
2π |
|
||||||||||||||
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ния интеграла вероятности в Mathcad применяется функция pnorm(x, μ,σ ), которая вычисляет интеграл
1 |
x |
− |
1 |
|
(t−μ)2 |
|
2 |
||||
|
∫ |
e 2σ |
|
dt . При значениях параметров μ =1 и σ =1 |
|
2π σ |
|
||||
−∞ |
|
|
|
|
|
|
|
|
|
|
|
функция pnorm вычисляет функцию Лапласа.
Рассмотрим применение данной формулы на следующей практической задаче.
Пример. При установившемся технологическом процессе предприятие выпускает в среднем 70% деталей высшего качества. Определить вероятность того, что из 10000 изделий число изделий высшего качества будет заключено между 6900 и 7100.
Напишем программу, решающую данную задачу двумя способами, используя интегральную теорему Лапласа (6.9) и формулу Бернулли (6.6).
Начало программы.
n :=10000 p := 0.7 q :=1− p k1:= 6900 k2 := 7100
x1:= |
k1−n p |
x2 := |
k2 −n p |
|
|
n p q |
n p q |
||||
|
|
||||
|
|
|
|
k 2 |
|
PL := pnorm(x2,0,1) − pnorm(x1,0,1) PB := ∑ dbinom(k,n, p) |
|||||
|
|
|
|
k =k1 |
|
PL = 0.9709 |
PB = 0.9717 | PL − PB |= 0.000802. |
||||
Конец программы.
Полученные результаты показывают хорошее совпадение вероятностей, полученных по интегральной теореме Лапласа PL и по формуле Бернулли PB.
102
Задание для самостоятельной работы.
1. Произведено n повторных испытаний, в каждом из которых вероятность происхождения некоторого случайного события A постоянна и равна p.
а) Используя формулу Бернулли и локальную теорему Лапласа, найти вероятность того, что событие A произойдет ровно k раз.
б) Вывести график функции распределения и многоугольник распределения данной случайной величины.
в) Найти наивероятнейшее число появления события A.
г) Исследовать процесс сходимости результатов локальной теоремы Лапласа и формулы Бернулли при увеличении числа испытаний n до величины n=10000, при этом k принять равным np. Выяснить при каком значении числа испытаний n результаты, полученные по двум формулам, отличаются менее чем на 1%.
№ |
p |
n |
k |
№ |
p |
n |
k |
№ |
p |
n |
k |
1 |
0,1 |
10 |
2 |
11 |
0,2 |
12 |
3 |
21 |
0,3 |
13 |
4 |
2 |
0,2 |
12 |
4 |
12 |
0,3 |
11 |
6 |
22 |
0,4 |
13 |
6 |
3 |
0,3 |
15 |
5 |
13 |
0,4 |
12 |
3 |
23 |
0,5 |
12 |
3 |
4 |
0,4 |
18 |
6 |
14 |
0,5 |
14 |
4 |
24 |
0,6 |
10 |
3 |
5 |
0,5 |
11 |
4 |
15 |
0,6 |
10 |
3 |
25 |
0,7 |
10 |
4 |
6 |
0,6 |
14 |
4 |
16 |
0,7 |
12 |
9 |
26 |
0,8 |
12 |
6 |
7 |
0,7 |
15 |
9 |
17 |
0,8 |
11 |
7 |
27 |
0,9 |
15 |
8 |
8 |
0,8 |
12 |
8 |
18 |
0,9 |
15 |
7 |
28 |
0,1 |
12 |
3 |
9 |
0,9 |
10 |
7 |
19 |
0,1 |
13 |
3 |
29 |
0,2 |
15 |
6 |
10 |
0,1 |
16 |
3 |
20 |
0,2 |
17 |
5 |
30 |
0,3 |
18 |
2 |
2. Произведено n повторных испытаний, в каждом из которых вероятность происхождения некоторого случайного события A постоянна и равна p.
a) Используя формулу Бернулли и локальную теорему Лапласа, найти вероятность того, что событие A произойдет ровно k раз.
|
б) |
Используя |
формулу Бернулли и интегральную теорему |
||||||||||
Лапласа, найти вероятность того, что событие A произойдет в |
|||||||||||||
диапазоне от k1 до k2 раз. |
|
|
|
|
|
|
|
||||||
№ |
p |
|
n |
k |
|
k1 |
k2 |
№ |
p |
n |
k |
k1 |
k2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
103 |
1 |
0,1 |
1000 |
100 |
100 |
120 |
16 |
0,7 |
1200 |
850 |
800 |
900 |
2 |
0,2 |
2000 |
402 |
400 |
450 |
17 |
0,8 |
1100 |
888 |
800 |
850 |
3 |
0,3 |
3000 |
895 |
880 |
920 |
18 |
0,9 |
1000 |
909 |
800 |
900 |
4 |
0,4 |
2000 |
790 |
750 |
800 |
19 |
0,1 |
3000 |
310 |
300 |
400 |
5 |
0,5 |
1000 |
502 |
400 |
520 |
20 |
0,2 |
4000 |
795 |
0 |
750 |
6 |
0,6 |
1500 |
895 |
900 |
990 |
21 |
0,3 |
1000 |
320 |
320 |
900 |
7 |
0,7 |
1100 |
772 |
0 |
770 |
22 |
0,4 |
2000 |
810 |
810 |
910 |
8 |
0,8 |
900 |
715 |
600 |
700 |
23 |
0,5 |
1800 |
890 |
890 |
920 |
9 |
0,9 |
1000 |
904 |
800 |
900 |
24 |
0,6 |
1400 |
800 |
800 |
850 |
10 |
0,1 |
5000 |
510 |
500 |
900 |
25 |
0,7 |
1000 |
710 |
690 |
710 |
11 |
0,2 |
3000 |
595 |
600 |
700 |
26 |
0,8 |
1200 |
950 |
0 |
950 |
12 |
0,3 |
1600 |
485 |
400 |
500 |
27 |
0,9 |
800 |
700 |
700 |
750 |
13 |
0,4 |
1000 |
403 |
400 |
485 |
28 |
0,1 |
4000 |
405 |
405 |
525 |
14 |
0,5 |
2000 |
998 |
950 |
998 |
29 |
0,2 |
4500 |
905 |
0 |
950 |
15 |
0,6 |
1500 |
902 |
900 |
925 |
30 |
0,3 |
3000 |
910 |
890 |
990 |
Геометрическое распределение. Пусть проводится n по-
вторных испытаний Бернулли. Рассмотрим случайную величину ξ – число испытаний до первого появления события A. Эта величина является дискретной случайной величиной, принимающей значение на множестве целых неотрицательных значений от 0 до ∞, и ее распределение определяется формулой:
p = P(ξ = k) = qk p, k = 0,1,2, , 0 < p <1, |
q =1− p. |
(6.10) |
|
k |
|
|
|
Используя формулу суммы бесконечной геометрической по- |
|||
∞ |
p |
|
|
следовательности, легко доказать, что ∑pk = |
=1. |
|
|
1−q |
|
||
k=0 |
|
|
|
В Mathcad для работы с геометрическим распределением встроены две функции: dgeom(k, p) – функция, возвращающая значения вероятностей pk ; pgeom(k, p) – функция распределения
вероятностей F(x).
Пример. Вероятность поражения цели при одном выстреле равна 0,2. Для случайной величины ξ , обозначающей число вы-
стрелов до первого попадания в цель, построить график функции распределения и многоугольник распределения. Найти вероятность того, что число выстрелов до первого попадания будет:
1) попадут с первого выстрела; 2) попадут с 5 выстрела;
104

3) попадут с 10 выстрела. Начало программы.
n :=100 |
p := 0.2 |
k := 0..n Pk := dgeom(k, p) |
Xk := k |
∑P =1 |
F(x) := pgeom(x, p) F(0) = 0.2 |
F(4) = 0.672 F(9) = 0.893
Конец программы.
Задание для самостоятельной работы
Вероятность поражения цели при одном выстреле равна p. Для случайной величины ξ , обозначающей число выстрелов до
первого попаданий в цель, построить график функции распределения и многоугольник распределения. Найти вероятность того, что число выстрелов до первого попадания будет:
1) попадут с k1 выстрела; 2) попадут с k2 выстрела; 3) число
выстрелов до первого попадания в цель будет заключено между k1 и k2 .
№ |
p |
k1 |
k2 |
№ |
p |
k1 |
k2 |
№ |
p |
k1 |
k2 |
1 |
0,04 |
10 |
35 |
11 |
0,14 |
7 |
25 |
21 |
0,24 |
4 |
15 |
2 |
0,05 |
10 |
34 |
12 |
0,15 |
7 |
24 |
22 |
0,25 |
3 |
14 |
3 |
0,06 |
10 |
33 |
13 |
0,16 |
6 |
23 |
23 |
0,26 |
3 |
13 |
4 |
0,07 |
9 |
32 |
14 |
0,17 |
6 |
22 |
24 |
0,27 |
3 |
12 |
5 |
0,08 |
9 |
31 |
15 |
0,18 |
6 |
21 |
25 |
0,28 |
2 |
11 |
6 |
0,09 |
9 |
30 |
16 |
0,19 |
5 |
20 |
26 |
0,29 |
2 |
10 |
7 |
0,10 |
8 |
29 |
17 |
0,20 |
5 |
19 |
27 |
0,30 |
1 |
9 |
8 |
0,11 |
8 |
28 |
18 |
0,21 |
5 |
18 |
28 |
0,31 |
1 |
8 |
9 |
0,12 |
8 |
27 |
19 |
0,22 |
4 |
17 |
29 |
0,32 |
0 |
7 |
10 |
0,13 |
7 |
26 |
20 |
0,23 |
4 |
16 |
30 |
0,33 |
0 |
6 |
105

Гипергеометрическое распределение . Классическим при-
мером для применения гипергеометрического распределения является следующая задача.
Пусть в партии из N изделий имеются M доброкачественных, а все остальные дефектные. Если из всей партии выбрать случайным образом n изделий, то число доброкачественных изделий в этой партии будет случайной величиной, которую обозначим ξ .
Для заданных величин N, M<N и n<N гипергеометрическое распределение имеет вид:
|
|
k n−k |
|
|
p |
= P(ξ = k) = |
CM CN −M |
, k = 0,1,2, min(n, M ) . |
(6.10) |
|
||||
k |
|
CNn |
|
|
|
|
|
||
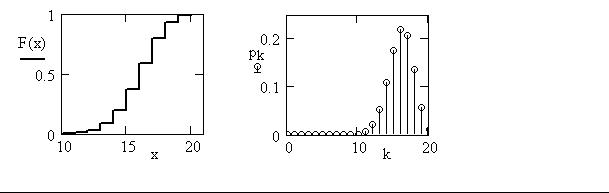
Пример. На заводской склад поступила партия из 1000 деталей, причем 800 из них высшего сорта. Из этой партии случайным образом выбрали 20 деталей. Найти вероятность, что число деталей высшего сорта будет больше 15. Вывести график функции распределения F(x) и многоугольник распределения.
Начало программы.
N :=1000 M :=800 n := 20 k := 0..min(n, M )
pk := |
combin(M ,k) combin(N − M ,n −k) |
max( p) = 0.22 |
∑p =1 |
||||||
|
|
|
|
||||||
|
|
|
|
|
combin(N,n) |
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
PA := ∑ pk |
PA = 0.630096 |
p16 = 0.22 |
|
||||||
|
k =16 |
|
|
|
|
|
|||
Подпрограмма для функции распределения. |
|
|
|||||||
F (x) := |
|
s ← 0 |
|
|
|
|
|
||
|
|
|
|
|
|
||||
|
|
|
i ← 0 |
|
|
|
|
|
|
|
|
|
while |
x > i |
|
|
|
|
|
|
|
|
|
s ← s + pi |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
i ←i +1 |
|
|
|
|
|
|
|
|
|
break if i > n |
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
График функции распределения F(x) и многоугольника распределения Pk .
106
Конец программы.
Таким образом, искомая вероятность равна 0,63. Из графика многоугольника распределения видно, что наиболее вероятное число деталей высшего сорта в данной выборке, с вероятностью
0,22, равно 16.
Задание для самостоятельной работы
На заводской склад поступила партия из N деталей, причем M из них высшего сорта. Из этой партии случайным образом выбрали n деталей. Найти вероятность, что число деталей высшего сорта будет в диапазоне от k1 до k2 . Вывести график функции
распределения F(x) и многоугольник распределения.
№ |
N |
M |
n |
k1 |
k2 |
№ |
N |
M |
n |
k1 |
k2 |
1 |
2000 |
1900 |
90 |
85 |
90 |
16 |
2000 |
100 |
20 |
2 |
5 |
2 |
1900 |
1700 |
85 |
75 |
80 |
17 |
1900 |
150 |
25 |
1 |
6 |
3 |
1800 |
1500 |
80 |
60 |
70 |
18 |
1800 |
200 |
30 |
2 |
7 |
4 |
1700 |
1300 |
75 |
50 |
60 |
19 |
1700 |
300 |
35 |
5 |
11 |
5 |
1600 |
1100 |
70 |
45 |
52 |
20 |
1600 |
400 |
40 |
9 |
17 |
6 |
1500 |
1000 |
65 |
40 |
47 |
21 |
1500 |
500 |
45 |
16 |
40 |
7 |
1400 |
800 |
60 |
30 |
38 |
22 |
1400 |
600 |
50 |
20 |
30 |
8 |
1300 |
700 |
55 |
27 |
33 |
23 |
1300 |
700 |
55 |
30 |
40 |
9 |
1200 |
400 |
50 |
16 |
22 |
24 |
1200 |
850 |
60 |
40 |
55 |
10 |
1100 |
300 |
45 |
10 |
15 |
25 |
1100 |
900 |
65 |
53 |
60 |
11 |
1000 |
200 |
40 |
7 |
11 |
26 |
1000 |
850 |
70 |
60 |
65 |
12 |
900 |
100 |
35 |
2 |
6 |
27 |
900 |
800 |
75 |
65 |
70 |
13 |
800 |
50 |
30 |
0 |
5 |
28 |
800 |
700 |
80 |
70 |
80 |
14 |
700 |
40 |
25 |
2 |
4 |
29 |
700 |
650 |
85 |
75 |
80 |
15 |
600 |
30 |
20 |
1 |
5 |
30 |
600 |
550 |
90 |
80 |
85 |
107
Распределение Пуассона. Пуассоновское распределение имеет случайная величина μ, принимающая целые неотрица-
тельные значения k = 0,1,2, |
с вероятностями |
|
||
p = P(μ = k) = λk e−λ |
, |
k = 0,1,2, ,n, , |
(6.12) |
|
k |
k! |
|
|
|
|
|
|
|
|
где λ > 0 – параметр пуассоновского распределения. При любых
∞
положительных значениях λ выполняется условие ∑pk =1.
k=0
Как известно, формула Пуассона применяется как предельный случай формулы Бернулли при больших значениях числа испытаний n и малых значениях вероятности p. При этом в качестве параметра λ применяется величина λ = np .
В Mathcad для работы с пуассоновским распределением встроены две функции: dpois(k, λ) – функция, возвращающая значения вероятностей pk ; функция ppois(k, λ) – возвращающая
функцию распределения F(x).
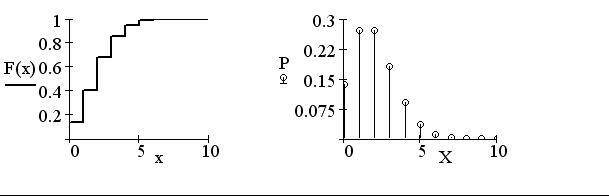
Пример. На завод прибыла партия деталей в количестве 2000шт. Вероятность того, что деталь окажется бракованной, равна 0,001. Какова вероятность того, что среди прибывших деталей будет менее 5 бракованных?
Программа на Mathcad, решающая данную задачу, имеет вид: Начало программы.
|
|
||
n := 2000 p := 0.001 λ := p n |
k := 0..n |
||
Pk := dpois(k,λ) Xk |
:= k |
∑P =1 |
|
PT = (0.135 0.271 |
0.271 |
0.18 |
0.09 0.036 0.012 7 10−3 ) |
|
4 |
|
|
F(x) := ppois(x,λ) |
∑Pk = 0.947 |
F (4.5) = 0.947 |
|
k=0
Конец программы.
108
