
- •1.Матрицы и операции над ними.
- •2.Определители и их свойства.
- •3.Ранг матрицы.
- •4.Обратная матрица
- •5.Решение систем линейных алгебраических уравнений по формуле крамера.
- •6.Решение систем линейных алгебраических уравнений матричным методом.
- •8.Линейные операции над векторами.
- •10.Скалярное произведение вектора.
- •11. Векторное произведение векторов
- •12. Смешанное произведение векторов.
- •13. Понятие о линейном векторном пространстве
- •14. Базис. Собственные числа. Собственные вектора.
- •15. Простейшие задачи на плоскости (деление отрезка в заданном соотношении, расстояние между двумя точками).
- •16. Прямая на плоскости. Расстояние от точки до прямой. Угол между прямыми.
- •19. Прямая в пространстве, канонические уравнения
- •20. Элементы теории множеств
- •1. Логические символы
- •2. Операции над множествами
- •21. Функция, область определения, способы задания. Сложная и обратная функции
- •22. Предел функции
- •23. Основные теоремы о пределах
- •24. Замечательные пределы
- •1. Пусть . Каждое значение X заключено между двумя положительными целыми числами:, где— это целая часть X.
- •2. Пусть . Сделаем подстановку, тогда
- •25. Бесконечно малые и бесконечно большие функции и их свойства
- •28. Производная и дифференциал функции одной переменной.
- •30. Правила вычисления производных (диффиринцирования).
- •31. Таблица производных.
- •32.Производная сложных и обратных функций.
- •Геометрический смысл дифференциала
- •36. (Правило Лопиталя).
- •39. Понятие экстремума, основные теоремы.
- •Необходимое условие экстремума
- •Первое достаточное условие экстремума
- •Второе достаточное условие экстремума
- •40. Выпуклость и вогнутость, точки перегиба, асимптоты.
- •Теоремы о выпуклости функции и точках перегиба
- •41. Исследование функции и построение графика.
- •42. Наибольшее и наименьшее значение функции, непрерывной на отрезке.
- •44. Неопределенный интеграл, свойства.
- •45. Таблица интегралов
- •46. Основные методы интегрирования.
- •Свойства
- •49. Замена переменной, интегрирование по частям.
31. Таблица производных.
32.Производная сложных и обратных функций.
Пусть
теперь задана сложная
функция ![]() ,
т.е. переменная
,
т.е. переменная![]() есть
функция переменной
есть
функция переменной![]()
![]() ,
а переменная
,
а переменная![]() есть,
в свою очередь, функция от независимой
переменной
есть,
в свою очередь, функция от независимой
переменной![]() .
.
Теорема. Если ![]() и
и![]() дифференцируемые функции
своих аргументов, то сложная
функция
дифференцируемые функции
своих аргументов, то сложная
функция ![]() является
дифференцируемой функцией и ее
производная равна произведению
производной данной функции по
промежуточному аргументу и производной
промежуточного аргумента по
независимой переменной:
является
дифференцируемой функцией и ее
производная равна произведению
производной данной функции по
промежуточному аргументу и производной
промежуточного аргумента по
независимой переменной:
![]() .
.
Утверждение
легко получается из очевидного
равенства ![]() (справедливого
при
(справедливого
при![]() и
и![]() )
предельным переходом при
)
предельным переходом при![]() (что
в силу непрерывности дифференцируемой
функции влечет
(что
в силу непрерывности дифференцируемой
функции влечет![]() ).
).
Перейдем к рассмотрению производной обратной функции.
Пусть
на множестве ![]() дифференцируемая
функция
дифференцируемая
функция![]() имеет
множество значений
имеет
множество значений![]() и
на множестве
и
на множестве![]() существуетобратная
функция
существуетобратная
функция ![]() .
.
Теорема. Если
в точке ![]() производная
производная![]() ,
то производная обратной функции
,
то производная обратной функции![]() в
точке
в
точке![]() существует
и равна обратной величине производной
данной функции:
существует
и равна обратной величине производной
данной функции: 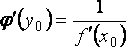 ,
или
,
или
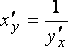 .
.
33.Дифференциал
функции,
его геометрический смысл, правило
вычисления дифференциалов. Дифференциалом
функции называется
линейная относительно ![]() часть
приращения функции. Она обозначается
как
часть
приращения функции. Она обозначается
как ![]() или
или ![]() .
Таким образом:
.
Таким образом:
![]()
Формулу для дифференциала функции можно записать в виде:
![]()
Отсюда получаем, что
![]()
Итак, это означает, что производная может быть представлена как обыкновенная дробь - отношение дифференциалов функции и аргумента.
Геометрический смысл дифференциала
Дифференциал
функции в точке ![]() равен
приращению ординаты касательной,
проведенной к графику функции в этой
точке, соответствующему приращению
аргумента
равен
приращению ординаты касательной,
проведенной к графику функции в этой
точке, соответствующему приращению
аргумента ![]() .
.
Правила вычисления:
1. Константу можно выносить за знак дифференциала.
![]()
2. Дифференциал суммы/разности.
Дифференциал суммы/разности функций равен суме/разности дифференциалов от каждого из слагаемых.
![]()
3. Дифференциал произведения.
![]()
4. Дифференциал частного.
![]()
5. Дифференциал константы равен нулю.
![]()
34.Производные и дефферинциалы высших порядков. Пусть производная некоторой функции f дифференцируема. Тогда производная от производной этой функции называется второй производной функции f и обозначается f". Таким образом,
f"(x) = (f'(x))'.
Если дифференцируема (n - 1)-я производная функции f, то ее n-й производной называется производная от (n - 1)-й производной функции f и обозначается f(n). Итак,
f(n)(x) = (f(n-1)(x))', n ϵ N, f(0)(x) = f(x).
Число n называется порядком производной.
Дифференциалом n-го порядка функции f называется дифференциал от дифференциала (n - 1)-го порядка этой же функции. Таким образом,
dnf(x) = d(dn-1f(x)), d0f(x) = f(x), n ϵ N.
Если x - независимая переменная, то
dx = const и d2x = d3x = ... = dnx = 0.
В этом случае справедлива формула
dnf(x) = f(n)(x)(dx)n.
36. (Правило Лопиталя).
Пусть
функции ![]() и
и ![]() удовлетворяют
следующим условиям:
удовлетворяют
следующим условиям:
1)
эти функции дифференцируемы в окрестности
точки ![]() ,
кроме, может быть, самой точки
,
кроме, может быть, самой точки ![]() ;
;
2) ![]() и
и ![]() в
этой окрестности;
в
этой окрестности;
3) ![]() ;
;
4) ![]() существует
конечный или бесконечный.
существует
конечный или бесконечный.
Тогда
существует и ![]() ,
причем
,
причем ![]()
Правило
Лопиталя распространяется и на случай ![]() .
Чтобы убедится в этом, достаточно
сделать замену
.
Чтобы убедится в этом, достаточно
сделать замену ![]() и
воспользоваться результатом выше
приведенной теоремы.
и
воспользоваться результатом выше
приведенной теоремы.
37.
Теоремы Коши, Ланранжа, Ролля
Теорема
Ролля. (О
нуле производной функции, принимающей
на концах отрезка равные значения)
Пусть
функция ![]()
непрерывна на отрезке
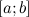 ;
;дифференцируема на интервале
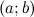 ;
;на концах отрезка
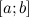 принимает
равные значения
принимает
равные значения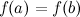 .
.
Тогда
на интервале ![]() найдется,
по крайней мере, одна точка
найдется,
по крайней мере, одна точка![]() ,
в которой
,
в которой![]() .
.
Следствие. (Геометрический смысл теоремы Ролля)
Найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс.
Если ![]() ,
то теорему Ролля можно сформулировать
следующим образом: между двумя
последовательными нулями дифференцируемой
функции имеется, хотя бы один, нуль
производной. (Следствие.)
,
то теорему Ролля можно сформулировать
следующим образом: между двумя
последовательными нулями дифференцируемой
функции имеется, хотя бы один, нуль
производной. (Следствие.)
Теорема Лагранжа. (О конечных приращениях)
Пусть
функция ![]()
непрерывна на отрезке
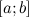 ;
;дифференцируема на интервале
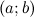 .
.
Тогда
на интервале ![]() найдется
по крайней мере одна точка
найдется
по крайней мере одна точка![]() ,
такая, что
,
такая, что
![]()
Теорема
Ролля есть частный случай теоремы
Лагранжа, когда ![]() .
(Замечание)
.
(Замечание)
Следствие. (Геометрический смысл теоремы Лагранжа)
На
кривой ![]() между
точками
между
точками![]() и
и![]() найдется
точка
найдется
точка![]() ,
такая, что через эту точку можно провести
касательную, параллельную хорде
,
такая, что через эту точку можно провести
касательную, параллельную хорде![]() (рис.
1).
(рис.
1).

Доказанная формула называется формулой Лагранжа или формулой конечных приращений. Она может быть переписана в виде:
![]()
Теорема Коши. (Об отношении конечных приращений двух функций)
Если
функции ![]() и
и![]() :
:
непрерывны на отрезке
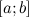 ;
;дифференцируемы на интервале
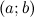 ;
;производная
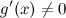 на
интервале
на
интервале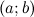 ,
,
тогда
на этом интервале найдется по крайней
мере одна точка ![]() ,
такая, что
,
такая, что
![]()
Если производная функции равна нулю на некотором промежутке, то функция является постоянной на этом промежутке. (теорема) Если две функции имеют равные производные на некотором промежутке, то они на этом промежутке отличаются друг от друга на некоторое слагаемое. (теорема)
38. Монотонность. Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное[1]. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.
Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции.
Определения
Пусть
дана функция ![]() Тогда
Тогда
функция
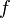 называетсявозраста́ющей на
называетсявозраста́ющей на 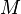 ,
если
,
если
![]() .
.
функция
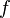 называетсястро́го
возраста́ющей на
называетсястро́го
возраста́ющей на 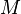 ,
если
,
если
![]() .
.
функция
 называетсяубыва́ющей на
называетсяубыва́ющей на 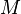 ,
если
,
если
![]() .
.
функция
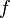 называетсястро́го
убыва́ющей на
называетсястро́го
убыва́ющей на 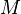 ,
если
,
если
![]() .
.
(Строго) возрастающая или убывающая функция называется (строго) монотонной.
Свойства монотонных функций
Монотонная функция, определённая на интервале, измерима относительно борелевских сигма-алгебр.
Монотонная функция,
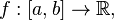 определённая
назамкнутом интервале, ограничена.
В частности, она интегрируема
по Лебегу.
определённая
назамкнутом интервале, ограничена.
В частности, она интегрируема
по Лебегу.Монотонная функция может иметь разрывы только первого рода. В частности, множество точек разрыва не более чем счётно.
Монотонная функция
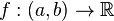 дифференцируема почти
всюду относительно меры
Лебега.
дифференцируема почти
всюду относительно меры
Лебега.
