15. Простейшие задачи на плоскости (деление отрезка в заданном соотношении, расстояние между двумя точками).

Если точка М(x, y, z) делит отрезок АВ, где А(x₁, y₁, z₁), В(x₂, y₂, z₂) в отношении λ=АМ:МВ, то координаты точки М определяются по формулам ,y и z аналогично.

Есть две произвольные точки A1(x1;y1;z1) и A2(x2;y2;z2) Тогда расстояние между точками A1 и A2 вычисляется так: 

16. Прямая на плоскости. Расстояние от точки до прямой. Угол между прямыми.

Нормальным вектором к плоскости, называется вектор N равный Ai+Bj+Ck, перпендикулярный к плоскости.

Прямая и плоскость в пространство могут:

• а) не иметь общих точек;

• б) иметь ровно одну общую точку;

• в) иметь хотя бы две общие точки.

Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую. Если задано уравнение прямой Ax + By + C = 0, то расстояние от точки M(Mx, My) до прямой можно найти, используя следующую формулу:

Угол между двумя прямыми (x-x₁)/m₁=(y-y₁)/n₁=(z-z₁)/p₁ и (x-x₂)/m₂=(y-y₂)/n₂=(z-z₂)/p₂ определяется следующим образом cosϕ=(m₁*m₂+n₁*n₂)+(p₁*p₂)/((√m₁²+n₁²+p₁²)*(√m₂²+n₂²+p₂²))

17. КРИВЫЕ 2-ОГО ПОРЯДКА: ЭЛЛИПС, ГИПЕРБОЛА, ПАРАБОЛА И ИХ КАНОНИЧЕСКИЕ УРАВНЕНИЯ.

Эллипсом называется геометрическое место всех точек плоскости, сумма расстояний от которых до фокусов есть величина постоянная, большая, чем расстояние между фокусами.

Пусть М (х;у) – произвольная точка эллипса. Т.к. MF₁ + MF₂ = 2a

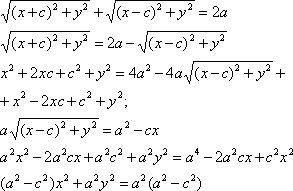
Т.к. То получаемИли

Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до фокусов есть величина постоянная. Пусть M(x;y) – произвольная точка гиперболы. Тогда согласно определению гиперболы |MF₁ – MF₂|=2a или MF₁ – MF₂ =±2a,

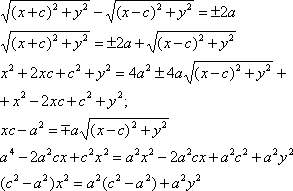
Парабола – множество всех точек плоскости, каждая из которых одинаково удалена от фокуса, и директрисы(фиксированное расстояние от фокуса). Расстояние между фокусом и директрисой называется параметром параболы и обозначается через р>0.

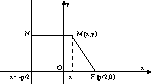Пусть M(x;y) – произвольная точка M с F. Проведем отрезок MN перпендикулярно

директрисе. Согласно определению MF=MN.

18. УРАВНЕНИЕ ПЛОСКОСТИ В ПРОСТРАНСТВЕ.

Пусть в пространстве Oxyz плоскость Q задана точкой и вектором, перпендикулярным этой плоскости (см. рис. 69). Выведем уравнение плоскости Q. Возьмем на ней произвольную точкуи составим вектор. При любом расположении точки Μ на плоскости Q векторыивзаимно перпендикулярны, поэтому их скалярное произведение равно нулю:, т. е.

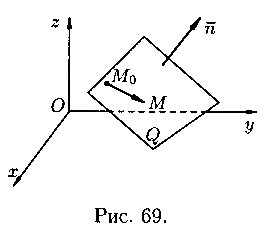
(12.3)

Координаты любой точки плоскости Q удовлетворяют уравнению (12.3), координаты точек, не лежащих на плоскости Q, этому уравнению не удовлетворяют (для них ).

Уравнение (12.3) называется уравнением  плоскости,   проходящей через данную точку  перпендикулярно вектору. Оно первой степени относительно текущих координат x, y, z. Векторназывается нормальным вектором плоскости.

Придавая коэффициентам А, В и С уравнения (12.3) различные значения, можно получить уравнение любой плоскости, проходящей череp точку . Совокупность плоскостей, проходящих через данную точку, называется связкой плоскостей, а уравнение (12.3) - уравнением связки плоскостей.