10. 10.Скалярное произведение вектора.

Скалярным произведением векторов a и b называется число равное произведению длин этих векторов на косинус угла между ними, т е a*b=|a|*|b|*cos(a^b), так же скалярное произведение вычисляется

A*b=a_xb_x+a_yb_y+a_zb_z

11. Векторное произведение векторов

Векторным произведением векторов a и b, называется вектор, обозначаемый a×b и удовлетворяющий следующим условиям

1. длина вектора a×b равна площади параллелограмма, построенного на векторах a и b, т е |a×b|=|a|×|b|*sin(a^b)

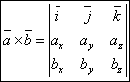
2. вектор |a×b|перпендикулярен b и a

3. вектора а,b,a×b образуют правую тройку, т е они ориентированы по отношению друг к другу как орты I,j, k

12. Смешанное произведение векторов.

Смешанным произведением векторов a, b,c называется скалярное произведение вектора (a×b)*c

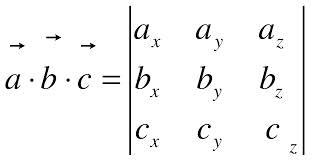
Смешанное произведение вектора по модулю равно объему параллелепипеда, построенному на этих векторах ν=|a×b|*c=|abc| находится по формуле 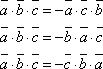Смешанное произведение меняет знак при перемене мест любых двух векторов-сомножителей. Смешанное произведение равно нулю тогда и только тогда, когда вектора коллинеарные. νтп=1/6 ν.

13. Понятие о линейном векторном пространстве

Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножение вектора на число, удовлетворяющее приведенным ниже 8 св-вам (рассматриваем как аксиомы), называется векторным пространством.

1. X+y=y+x-коммуникативное( переместительное) св-во суммы

2. (x+y)+z=(x+(y+z) – ассоциативное ( сочетательное) св-во суммы

3. α(βx)=(αβ)xассоциативное относительно числового множителя суммы

4. (x+y)=x+y –дистрибутивное ( распределительное) относительно суммы векторов св-во

5. (α+β)x=αx+βx – дистрибутивное относительно суммы числовых множителей св-во

6. Существует нулевой вектор такой, что X=0=x для любого вектора х

7. Для любого вектора х существует противоположный вектор (-х) такой, что (-х)+х=0

8. 1*х=х для любого вектора х

Следует отметить, что под x, y, z можно рассматривать не только векторы, но и элементы любой природы. В этом случае соответствующее множество элементов называется линейным пространством. Линейным пространством является, например, множество всех алгебраических многочленов степени, не превышающей натурального числа n. Легко убедится, что если x, и у- многочлены степени не выше n, то они обладают всеми 8 св-вами. заметим, что множество всех многочленов степени, точно равной натуральному числу n, не является линейным пространством, т к в нем не определена операция сложения, ибо сумма двух многочленов может оказаться многочленом степени ниже n. А множество многочленов степени не выше n, но с положительными коэффициентами так же не является линейным пространством, т к в нем нет операции умножения элемента на число: такие элементы нельзя умножать на отрицательные числа.

14. Базис. Собственные числа. Собственные вектора.

Базис-совокупность n линейно зависимых векторов n-мерного пространства R.

Линейное пространство R называется n-мерным, если в нем существует n линейно зависимых векторов, а любые из (n+1) векторов уже являются зависимыми. Другими словами, размерность пространства-это максимальное число, содержащийся в нем линейно зависимых векторов.

Векторы a_m называется линейной комбинацией векторов а₁,а₂…a_m-1 векторного пространства R, если он равен сумме произведений на произвольные действительные числа a_m=λ₁a₁+ λ₂a₂+…+λ_m-1a_m-1, где λ₁, λ₂,…,λ_m-1-какие угодно действительные числа. Векторы а₁,а₂…a_m векторного пространства R называются линейно зависимыми, если существуют такие числа λ₁, λ₂,…,λ_m не равные одновременно нулю, что λ₁a₁+ λ₂a₂+…+λ_ma_m=0 в противном случае векторы а₁,а₂…a_m называются линейно независимыми.

Число лямда λ-называется собственное числом матрицы А, если существует Х, такой что А*Х=λ*Х, при этом Х называется собственным вектором матрицы А соответствующим собственному числу λ. Характерным уравнением матрицы А, называется уравнение вид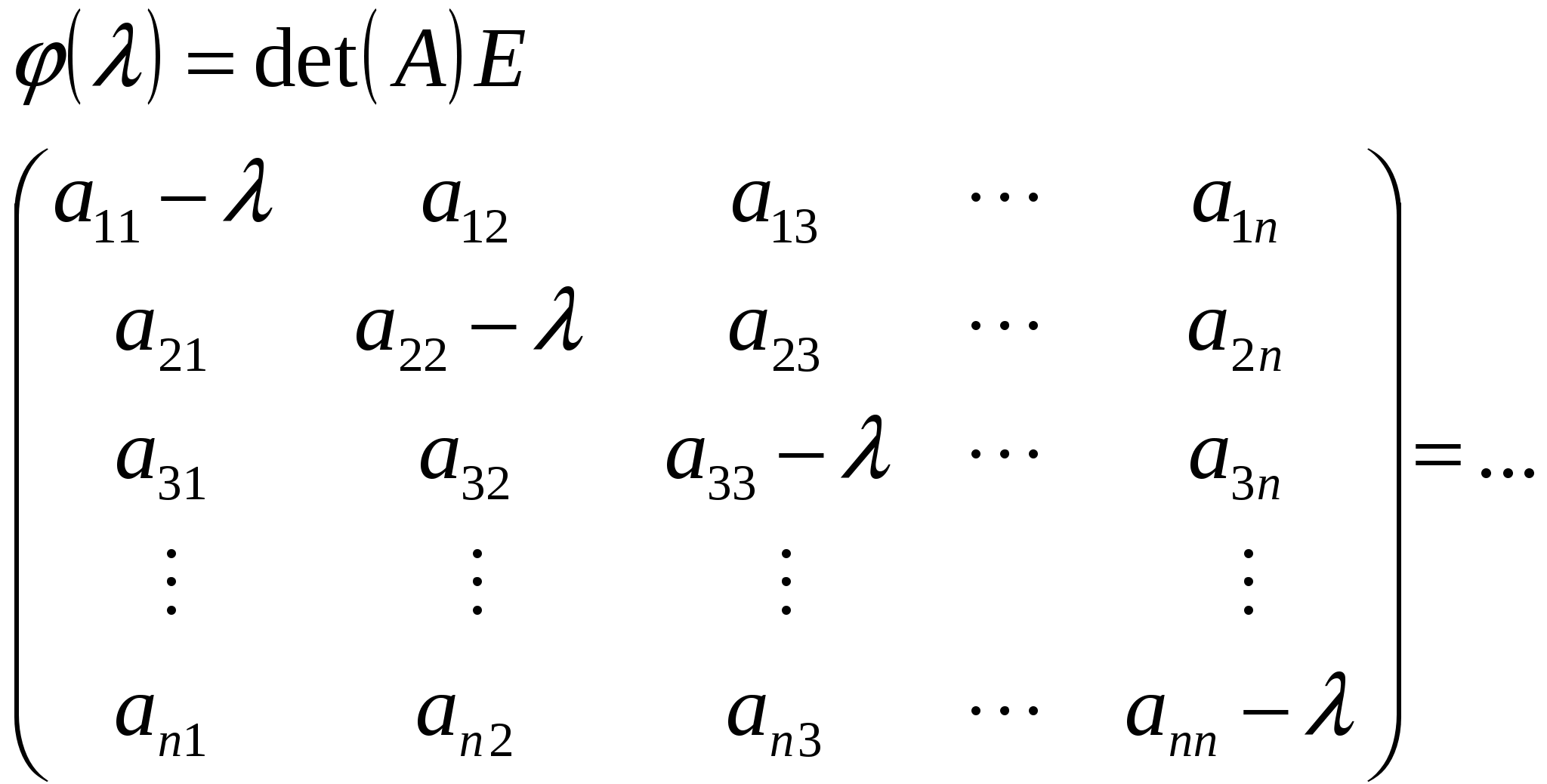а корни этого уравнения λ₁, λ₂,…,λ_m являются собственными числами матрицы А.