
- •1.Матрицы и операции над ними.
- •2.Определители и их свойства.
- •3.Ранг матрицы.
- •4.Обратная матрица
- •5.Решение систем линейных алгебраических уравнений по формуле крамера.
- •6.Решение систем линейных алгебраических уравнений матричным методом.
- •8.Линейные операции над векторами.
- •10.Скалярное произведение вектора.
- •11. Векторное произведение векторов
- •12. Смешанное произведение векторов.
- •13. Понятие о линейном векторном пространстве
- •14. Базис. Собственные числа. Собственные вектора.
- •15. Простейшие задачи на плоскости (деление отрезка в заданном соотношении, расстояние между двумя точками).
- •16. Прямая на плоскости. Расстояние от точки до прямой. Угол между прямыми.
- •19. Прямая в пространстве, канонические уравнения
- •20. Элементы теории множеств
- •1. Логические символы
- •2. Операции над множествами
- •21. Функция, область определения, способы задания. Сложная и обратная функции
- •22. Предел функции
- •23. Основные теоремы о пределах
- •24. Замечательные пределы
- •1. Пусть . Каждое значение X заключено между двумя положительными целыми числами:, где— это целая часть X.
- •2. Пусть . Сделаем подстановку, тогда
- •25. Бесконечно малые и бесконечно большие функции и их свойства
- •28. Производная и дифференциал функции одной переменной.
- •30. Правила вычисления производных (диффиринцирования).
- •31. Таблица производных.
- •32.Производная сложных и обратных функций.
- •Геометрический смысл дифференциала
- •36. (Правило Лопиталя).
- •39. Понятие экстремума, основные теоремы.
- •Необходимое условие экстремума
- •Первое достаточное условие экстремума
- •Второе достаточное условие экстремума
- •40. Выпуклость и вогнутость, точки перегиба, асимптоты.
- •Теоремы о выпуклости функции и точках перегиба
- •41. Исследование функции и построение графика.
- •42. Наибольшее и наименьшее значение функции, непрерывной на отрезке.
- •44. Неопределенный интеграл, свойства.
- •45. Таблица интегралов
- •46. Основные методы интегрирования.
- •Свойства
- •49. Замена переменной, интегрирование по частям.
39. Понятие экстремума, основные теоремы.
Точка ![]() называется точкой
локального максимума функции
называется точкой
локального максимума функции ![]() ,
если существует такая окрестность этой
точки, что для всех
,
если существует такая окрестность этой
точки, что для всех ![]() из
этой окрестности выполняется
неравенство:
из
этой окрестности выполняется
неравенство: ![]() .
.
Точка ![]() называется точкой
локального минимума функции
называется точкой
локального минимума функции ![]() ,
если существует такая окрестность этой
точки, что для всех
,
если существует такая окрестность этой
точки, что для всех ![]() из
этой окрестности
из
этой окрестности ![]() .
.
Значение функции в точке максимума называется локальным максимумом, значение функции в точке минимума -локальным минимумом данной функции. Локальные максимум и минимум функции называются локальными экстремумами.
Точка ![]() называется
точкой строгого
локального максимума функции
называется
точкой строгого
локального максимума функции ![]() ,
если для всех
,
если для всех ![]() из
окрестности этой точки будет справедливо
строгое неравенство
из
окрестности этой точки будет справедливо
строгое неравенство ![]() .
.
Точка ![]() называется
точкой строгого
локального минимума функции
называется
точкой строгого
локального минимума функции ![]() ,
если для всех
,
если для всех ![]() из
окрестности этой точки будет справедливо
строгое неравенство
из
окрестности этой точки будет справедливо
строгое неравенство ![]() .
.
Наибольшее или наименьшее значение функции на промежутке называется глобальным экстремумом.
Необходимое условие экстремума
Теорема
(Необходимое условие экстремума)
Если
функция ![]() имеет
экстремум в точке
имеет
экстремум в точке ![]() ,
то ее производная
,
то ее производная ![]() либо
равна нулю, либо не существует.
либо
равна нулю, либо не существует.
Точки,
в которых производная равна нулю: ![]() ,
называются стационарными
точками функции.
,
называются стационарными
точками функции.
Точки,
в которых выполняется необходимое
условие экстремума для непрерывной
функции, называются критическими
точками этой
функции. То есть критические
точки -
это либо стационарные точки (решения
уравнения ![]() ),
либо это точки, в которых производная
),
либо это точки, в которых производная ![]() не
существует.
не
существует.
Первое достаточное условие экстремума
Теорема
(Первое достаточное условие экстремума)
Пусть
для функции ![]() выполнены
следующие условия:
выполнены
следующие условия:
функция непрерывна в окрестности точки
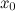 ;
;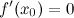 или
или 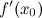 не
существует;
не
существует;производная
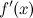 при
переходе через точку
при
переходе через точку 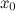 меняет
свой знак.
меняет
свой знак.
Тогда
в точке ![]() функция
функция ![]() имеет
экстремум, причем это минимум, если при
переходе через точку
имеет
экстремум, причем это минимум, если при
переходе через точку ![]() производная
меняет свой знак с минуса на плюс;
максимум, если при переходе через
точку
производная
меняет свой знак с минуса на плюс;
максимум, если при переходе через
точку ![]() производная
меняет свой знак с плюса на минус.
производная
меняет свой знак с плюса на минус.
Если
производная ![]() при
переходе через точку
при
переходе через точку ![]() не
меняет знак, то экстремума в точке
не
меняет знак, то экстремума в точке ![]() нет.
нет.
Таким
образом, для того чтобы исследовать
функцию ![]() на
экстремум, необходимо:
на
экстремум, необходимо:
найти производную
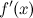 ;
;найти критические точки, то есть такие значения
 ,
в которых
,
в которых  или
или  не
существует;
не
существует;исследовать знак производной слева и справа от каждой критической точки;
найти значение функции в экстремальных точках.
Второе достаточное условие экстремума
Теорема
(Второе достаточное условие экстремума)
Пусть
для функции ![]() выполнены
следующие условия:
выполнены
следующие условия:
она непрерывна в окрестности точки
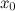 ;
;первая производная
 в
точке
в
точке 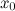 ;
; в
точке
в
точке 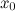 .
.
Тогда
в точке ![]() достигается
экстремум, причем, если
достигается
экстремум, причем, если ![]() ,
то в точке
,
то в точке ![]() функция
функция ![]() имеет
минимум; если
имеет
минимум; если ![]() ,
то в точке
,
то в точке ![]() функция
функция ![]() достигает
максимум.
достигает
максимум.
40. Выпуклость и вогнутость, точки перегиба, асимптоты.
График
функции ![]() ,
дифференцируемой на интервале
,
дифференцируемой на интервале ![]() ,
является на этом интервале выпуклым,
если график этой функции в пределах
интервала
,
является на этом интервале выпуклым,
если график этой функции в пределах
интервала ![]() лежит
не выше любой своей касательной (рис.
1).
лежит
не выше любой своей касательной (рис.
1).
График
функции ![]() ,
дифференцируемой на интервале
,
дифференцируемой на интервале ![]() ,
является на этом интервале вогнутым,
если график этой функции в пределах
интервала
,
является на этом интервале вогнутым,
если график этой функции в пределах
интервала ![]() лежит
не ниже любой своей касательной (рис.
2).
лежит
не ниже любой своей касательной (рис.
2).

