28. Производная и дифференциал функции одной переменной.

   Понятие производной. Свойства производной

При решении различных задач геометрии, механики, физики и других отраслей знания возникла необходимость с помощью одного и того же аналитического процесса из данной функции y=f(x) получать новую функцию, которую называют производной функцией (или просто производной) данной функции f(x) и обозначают символом

Тот процесс, с помощью которого из данной функции f(x) получают новую функцию f ' (x), называют дифференцированием и состоит он из следующих трех шагов:

1) даем аргументу x приращение ∆x и определяем соответствующее приращение функции  ∆y = f(x+∆x) -f(x);

       2) составляем отношение  3) считаяx постоянным, а ∆х→ 0, находим   , который обозначаем черезf ' (x), как бы подчеркивая тем самым, что полученная функция зависит лишь от того значения x, при котором мы переходим к пределу.

Определение:  Производной y ' =f ' (x) данной функции y=f(x) при данном x называется предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю, если, конечно, этот предел существует, т.е. конечен.

Таким образом,

 ,  или  

Заметим, что если при некотором значении x, например при x=a, отношение

 при ∆х→ 0 не стремится к конечному пределу, то в этом случае говорят, что функция f(x) при x=a (или в точке x=a) не имеет производной или не дифференцируема в точке x=a.

Свойства производных:

   1.     Если производные функции f и g в точке х₀ существуют, то существует и производная суммы f+g в этой точке, причем

(f+g)’ (х₀)=f’(х₀)+g’(х₀);

(производная суммы равна сумме производных)

   2.     Если производные функции f и g в точке х₀ существуют, то существует и производная произведения fg в этой точке, причем

(fg)’(х₀)=f’(х₀)g(х₀)+f(х₀)g’(х₀);

    3.     Если производные функции f и g в точке х₀ существуют и g(х₀) не равные 0, то существует и производная частного f/g в этой точке, причем 

       

В частности, если g(x)=c, то

(fc)’(х₀)=(cf)’(х₀)=cf’(х₀)

(постоянный множитель можно вынести за знак производной).

29. Производная, ее геометрический смысл.  Предел отношения приращения функции к приращению аргумента, при стремлении последнего к нулю, называют производной функции в данной точке:

Геометрический смысл производной заключается в том, что численно производная функции в данной точке равна тангенсу угла, образованного касательной, проведенной через эту точку к данной кривой, и положительным направлением оси Ох:

30. Правила вычисления производных (диффиринцирования).

Пусть функции и имеют производные в точке . Тогда

1. Константу можно выносить за знак производной.

2. Производная суммы/разности.

Производная суммы/разности двух функций равна сумме/разности производных от каждой из функций.

3. Производная произведения.

4. Производная частного.

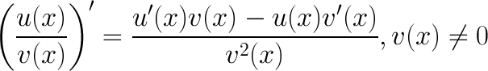
5. Производная сложной функции.

Производная сложной функции равна производной этой функции по промежуточному аргументу , умноженной на производную от промежуточного аргумента по основному аргументу .

 и имеют производные соответственно в точках и . Тогда

Теорема

(О производной обратной функции)

Если функция непрерывна и строго монотонна в некоторой окрестности точки и дифференцируема в этой точке, то обратная функция имеет производную в точке , причем .