- •1.Матрицы и операции над ними.
- •2.Определители и их свойства.
- •3.Ранг матрицы.
- •4.Обратная матрица
- •5.Решение систем линейных алгебраических уравнений по формуле крамера.
- •6.Решение систем линейных алгебраических уравнений матричным методом.
- •8.Линейные операции над векторами.
- •10.Скалярное произведение вектора.
- •11. Векторное произведение векторов
- •12. Смешанное произведение векторов.
- •13. Понятие о линейном векторном пространстве
- •14. Базис. Собственные числа. Собственные вектора.
- •15. Простейшие задачи на плоскости (деление отрезка в заданном соотношении, расстояние между двумя точками).
- •16. Прямая на плоскости. Расстояние от точки до прямой. Угол между прямыми.
- •19. Прямая в пространстве, канонические уравнения
- •20. Элементы теории множеств
- •1. Логические символы
- •2. Операции над множествами
- •21. Функция, область определения, способы задания. Сложная и обратная функции
- •22. Предел функции
- •23. Основные теоремы о пределах
- •24. Замечательные пределы
- •1. Пусть . Каждое значение X заключено между двумя положительными целыми числами:, где— это целая часть X.
- •2. Пусть . Сделаем подстановку, тогда
- •25. Бесконечно малые и бесконечно большие функции и их свойства
- •28. Производная и дифференциал функции одной переменной.
- •30. Правила вычисления производных (диффиринцирования).
- •31. Таблица производных.
- •32.Производная сложных и обратных функций.
- •Геометрический смысл дифференциала
- •36. (Правило Лопиталя).
- •39. Понятие экстремума, основные теоремы.
- •Необходимое условие экстремума
- •Первое достаточное условие экстремума
- •Второе достаточное условие экстремума
- •40. Выпуклость и вогнутость, точки перегиба, асимптоты.
- •Теоремы о выпуклости функции и точках перегиба
- •41. Исследование функции и построение графика.
- •42. Наибольшее и наименьшее значение функции, непрерывной на отрезке.
- •44. Неопределенный интеграл, свойства.
- •45. Таблица интегралов
- •46. Основные методы интегрирования.
- •Свойства
- •49. Замена переменной, интегрирование по частям.
1. Пусть . Каждое значение X заключено между двумя положительными целыми числами:, где— это целая часть X.
Отсюда
следует: ![]() ,
поэтому
,
поэтому
![]() .
.
Если ![]() ,
то
,
то![]() .
Поэтому, согласно пределу
.
Поэтому, согласно пределу![]() ,
имеем:
,
имеем:
![]()
![]() .
.
По
признаку (о пределе промежуточной
функции) существования пределов ![]() .
.
2. Пусть . Сделаем подстановку, тогда
![]()
![]() .
.
Из
двух этих случаев вытекает, что ![]() для
вещественного x.
для
вещественного x.![]()
Следствия
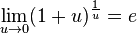

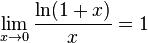
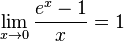
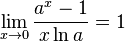 для
для 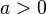 ,
,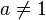
Доказательства следствий
![]()
25. Бесконечно малые и бесконечно большие функции и их свойства
Бесконечно малая
Последовательность ![]() называется бесконечно
малой, если
называется бесконечно
малой, если![]() .
Например, последовательность чисел
.
Например, последовательность чисел![]() —
бесконечно малая.
—
бесконечно малая.
Функция
называется бесконечно малой в
окрестности точки ![]() ,
если
,
если![]() .
.
Функция
называется бесконечно малой на
бесконечности, если ![]() либо
либо![]() .
.
Также
бесконечно малой является функция,
представляющая собой разность функции
и её предела, то есть если ![]() ,
то
,
то![]() ,
,![]() .
.
Бесконечно большая
Во
всех приведённых ниже формулах
бесконечность справа от равенства
подразумевается определённого знака
(либо «плюс», либо «минус»). То есть,
например, функция ![]() ,
неограниченная с обеих сторон, не
является бесконечно большой при
,
неограниченная с обеих сторон, не
является бесконечно большой при![]() .
.
Последовательность ![]() называется бесконечно
большой, если
называется бесконечно
большой, если![]() .
.
Функция
называется бесконечно большой в
окрестности точки ![]() ,
если
,
если![]() .
.
Функция
называется бесконечно большой на
бесконечности, если ![]() либо
либо![]()
Свойства бесконечно малых
Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
Произведение бесконечно малых — бесконечно малая.
Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.
Если
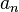 —
бесконечно малая последовательность,
сохраняющая знак, то
—
бесконечно малая последовательность,
сохраняющая знак, то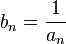 —
бесконечно большая последовательность.
—
бесконечно большая последовательность.
26.Непрерывная функция. Свойства непрерывных функций.Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.
Свойства
Локальные
Функция,
непрерывная в точке ![]() ,
является ограниченной в некоторой
окрестности этой точки.
,
является ограниченной в некоторой
окрестности этой точки.
Если функция
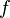 непрерывна
в точке
непрерывна
в точке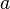 и
и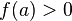 (или
(или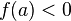 ),
то
),
то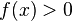 (или
(или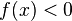 )
для всех
)
для всех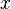 ,
достаточно близких к
,
достаточно близких к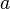 .
.Если функции
 и
и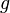 непрерывны
в точке
непрерывны
в точке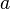 ,
то функции
,
то функции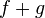 и
и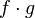 тоже
непрерывны в точке
тоже
непрерывны в точке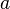 .
.Если функции
 и
и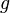 непрерывны
в точке
непрерывны
в точке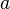 и
при этом
и
при этом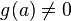 ,
то функция
,
то функция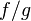 тоже
непрерывна в точке
тоже
непрерывна в точке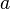 .
.Если функция
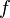 непрерывна
в точке
непрерывна
в точке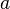 и
функция
и
функция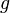 непрерывна
в точке
непрерывна
в точке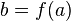 ,
то ихкомпозиция
,
то ихкомпозиция  непрерывна
в точке
непрерывна
в точке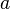 .
.
Глобальные
Функция, непрерывная на отрезке (или любом другом компактном множестве), равномерно непрерывна на нём.
Функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения.
Областью значений функции
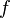 ,
непрерывной на отрезке
,
непрерывной на отрезке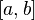 ,
является отрезок
,
является отрезок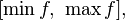 где
минимум и максимум берутся по отрезку
где
минимум и максимум берутся по отрезку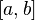 .
.Если функция
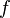 непрерывна
на отрезке
непрерывна
на отрезке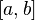 и
и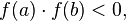 то
существует точка
то
существует точка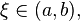 в
которой
в
которой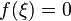 .
.Если функция
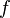 непрерывна
на отрезке
непрерывна
на отрезке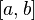 и
число
и
число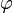 удовлетворяет
неравенству
удовлетворяет
неравенству или
неравенству
или
неравенству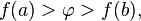 то
существует точка
то
существует точка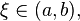 в
которой
в
которой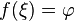 .
.Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна.
Монотонная функция на отрезке
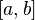 непрерывна
в том и только в том случае, когда
область ее значений является отрезком
с концами
непрерывна
в том и только в том случае, когда
область ее значений является отрезком
с концами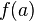 и
и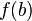 .
.Если функции
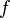 и
и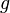 непрерывны
на отрезке
непрерывны
на отрезке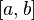 ,
причем
,
причем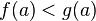 и
и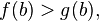 то
существует точка
то
существует точка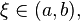 в
которой
в
которой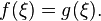 Отсюда,
в частности, следует, что любое
непрерывное отображение отрезка в
себя имеет хотя бы однунеподвижную
точку.
Отсюда,
в частности, следует, что любое
непрерывное отображение отрезка в
себя имеет хотя бы однунеподвижную
точку.
27.
Точки разрыва. Точки разрыва - Точка ![]() ,
в которой нарушено хотя бы одно из трех
условийнепрерывности
функции,
а именно:
,
в которой нарушено хотя бы одно из трех
условийнепрерывности
функции,
а именно:
функция
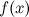 определена
в точке и ее окрестности;
определена
в точке и ее окрестности;существует конечный предел функции
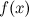 в
точке
в
точке ;
;это предел равен значению функции в точке
 ,
т.е.
,
т.е.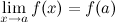
Если
в точке ![]() существуют
конечные пределы
существуют
конечные пределы ![]() и
и ![]() ,
такие, что
,
такие, что ![]() ,
то точка
,
то точка ![]() называется точкой
разрыва первого рода.
называется точкой
разрыва первого рода.
Если
хотя б один из пределов ![]() или
или ![]() не
существует или равен бесконечности,
то точка
не
существует или равен бесконечности,
то точка ![]() называется точкой
разрыва второго рода.
называется точкой
разрыва второго рода.
Если
существуют левый
и правый пределы функции в
точке и они равны друг другу, но не
совпадают со значением функции ![]() в
точке
в
точке ![]() :
: ![]() или
функция
или
функция ![]() не
определена в точке
не
определена в точке ![]() ,
то точка
,
то точка ![]() называется точкой
устранимого разрыва.
называется точкой
устранимого разрыва.