22. Предел функции

Определение предела по Коши. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого ε > 0 существует δ > 0 такое, что для всех x, удовлетворяющих условию |x – a| < δ, x ≠ a, выполняется неравенство |f (x) – A| < ε.

Определение предела по Гейне. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для любой последовательности такой, чтосходящейся к числуa, соответствующая последовательность значений функции сходится к числуA.

23. Основные теоремы о пределах

 

Теорема 1. (о предельном переходе в равенстве) Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.

Þ .

Теорема 2. (о предельном переходе в неравенстве) Если значения функции f(x) в окрестности некоторой точки не превосходят соответствующих значений функции g(x) , то предел функции f(x) в этой точке не превосходит предела функции g(x).

Þ .

Теорема 3. Предел постоянной равен самой постоянной.

.

Доказательство. f(x)=с,    докажем, что    .

Возьмем  произвольное e>0. В качестве d можно взять любое

положительное число. Тогда при 

.

Теорема 4. Функция не может иметь двух различных пределов в

одной точке.

Доказательство. Предположим противное. Пусть

и  .

По теореме о связи предела и бесконечно малой функции:

f(x)-A= - б.м. при ,

f(x)-B= - б.м. при .

Вычитая эти равенства, получим:

 B-A=-.

Переходя к пределам в обеих частях равенства при , имеем:

B-A=0, т.е. B=A. Получаем противоречие, доказывающее теорему.

Теорема 5. Если каждое слагаемое алгебраической суммы функций имеет предел при , то и алгебраическая сумма имеет предел при, причем предел алгебраической суммы равен алгебраической сумме пределов.

.

Доказательство. Пусть ,,.

Тогда, по теореме о связи предела и б.м. функции:

где - б.м. при.

Сложим алгебраически эти  равенства:

f(x)+g(x)-h(x)-(А+В-С)=,

где б.м. при.

По теореме о связи предела и б.м. функции:

А+В-С=.

Теорема 6. Если каждый из сомножителей произведения конечного числа функций имеет предел при , то и произведение имеет предел при, причем предел произведения равен произведению пределов.

.

Следствие. Постоянный множитель можно выносить за знак предела.

.

Теорема 7. Если функции f(x) и g(x) имеют предел при ,

причем , то и их частное имеет предел при, причем предел частного равен частному пределов.

,  .

24. Замечательные пределы

Замеча́тельные преде́лы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известных математических тождеств со взятием предела. Особенно известны:

• Первый замечательный предел:

• Второй замечательный предел:

Первый замечательный предел

Доказательство

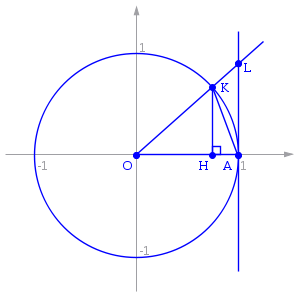
Рассмотрим односторонние пределы ии докажем, что они равны 1.

Пусть . Отложим этот угол на единичной окружности ().

Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке . ТочкаH — проекция точки K на ось OX.

Очевидно, что:

(1)

(где — площадь сектора)

(из :)

Подставляя в (1), получим:

Так как при :

Умножаем на :

Перейдём к пределу:

Найдём левый односторонний предел:

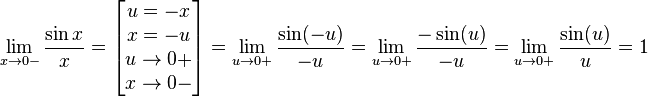
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.

Следствия

• 

• 

• 

• 

Доказательство следствий  

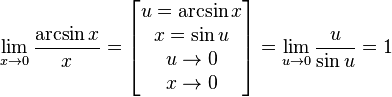
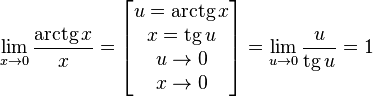
Второй замечательный предел

или 

Доказательство второго замечательного предела:

Доказательство для натуральных значений x  

Докажем вначале теорему для случая последовательности 

По формуле бинома Ньютона: 

Полагая , получим:

       (1)

Из данного равенства (1) следует, что с увеличением n число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении n число убывает, поэтому величинывозрастают. Поэтому последовательность—возрастающая, при этом

(2).

Покажем, что она ограничена. Заменим каждую скобку в правой части равенства на единицу, правая часть увеличится, получим неравенство

Усилим полученное неравенство, заменим 3,4,5, …, стоящие в знаменателях дробей, числом 2:

.

Сумму в скобке найдём по формуле суммы членов геометрической прогрессии:

.

Поэтому (3).

Итак, последовательность ограничена сверху, при этом выполняются неравенства (2) и (3):.

Следовательно, на основании теоремы Вейерштрасса (критерий сходимости последовательности) последовательность монотонно возрастает и ограниченна, значит имеет предел, обозначаемый буквойe. Т.е. 

Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что . Рассмотрим два случая: