• Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольцаили поля(например, целыхили комплексныхчисел), которая представляет собой совокупность строки столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы, в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими. Матрицы широко применяются в математике для компактной записи систем линейных алгебраическихилидифференциальныхуравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.

• Если у матрицы количество строк m совпадает с количеством столбцов n, то такая матрица называется квадратной, а число m = n называется размеромквадратной матрицы или её порядком. Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной.

• Для квадратных матриц существует единичная матрица E (аналог единицыдля операцииумножения чисел) такая, что умножение любой матрицы на неё не влияет на результат, а именно

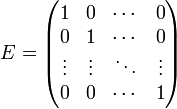
• EA = AE = A

• У единичной матрицы единицы стоят только по главной диагонали, остальные элементы равны нулю

• 2.Матрицы допускают следующие алгебраическиеоперации:

• сложениематриц, имеющих один и тот же размер;

• умножениематриц подходящего размера (матрицу, имеющуюn столбцов, можно умножить справа на матрицу, имеющую n строк);

• умножениематрицы на элемент основного кольца или поля (т. е.скаляр).

• Операции над матрицами

• Умножение матрицы на число

• Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен

• 

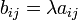
• Свойства умножения матриц на число

• 1*A = A;

• (Λβ)A = Λ(βA)

• (Λ+β)A = ΛA + βA

• Λ(A+B) = ΛA + ΛB

• Сложение матриц

• Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц Aи B, то есть каждый элемент матрицы C равен

• 

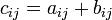
• Все свойства линейных операций , повторяют аксиомы линейного пространства и поэтому справедлива теорема:

• Множество всех матриц одинаковых размеров MxN образуют линейное пространство над полем P(полем всех действительных или комплексных чисел), поэтому каждая матрица является и вектором этого пространства.

• Умножение матриц

• Умножение матриц (обозначение: AB, реже со знаком умножения 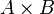) — есть операция вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

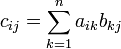
• Количество столбцов в матрице A должно совпадать с количеством строк в матрице B. Если матрица A имеет размерность 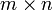, B — 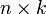, то размерность их произведения AB = C есть .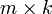

• Сложение и вычитание допускается только для матриц одинакового размера.

• Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть

• A + Θ = A

• Все элементы нулевой матрицы равны нулю.

• Возводить в степень можно только квадратные матрицы.

• Ассоциативностьсложения:A + (B + C) = (A + B) + C.

• Коммутативностьсложения:A + B = B + A.

• Ассоциативность умножения: A(BC) = (AB)C.

• Вообще говоря, умножение матриц некоммутативно: 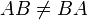. Используя это свойство, вводяткоммутаторматриц.

• Дистрибутивностьумножения относительно сложения:

• A(B + C) = AB + AC;

• (B + C)A = BA + CA.

• С учётом упомянутых выше свойств, матрицы образуют кольцоотносительно операций сложения и умножения.

• Свойства операции транспонирования матриц:

• (A^T)^T = A

• (AB)^T = B^TA^T

• (A ^{− 1})^T = (A^T) ^{− 1}, если обратная матрицаA ^{− 1} существует.

• (A + B)^T = A^T + B^T

• detA = detA^T

• 3.Определителем (детерминантом) матрицы называется значение нормированнойкососимметрической(антисимметрической)полилинейной формывалентности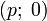на столбцах матрицы. Квадратная матрица над числовым полем вырождена тогда и только тогда, когда ее определитель равен нулю.

• Свойства определителей

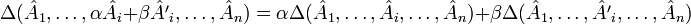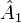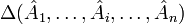• Определитель — кососимметричнаяполилинейная функция строк (столбцов) матрицы. Полилинейность означает, что определитель линеен по всем строкам (столбцам):, гдеи т. д. — строчки матрицы,— определитель такой матрицы.

• При добавлении к любой строке (столбцу) линейной комбинациидругих строк (столбцов) определитель не изменится.

• Если две строки (столбца) матрицы совпадают, то её определитель равен нулю.

• Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю.

• Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1).

• Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.

• Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю.

• Сумма произведений всех элементов любой строки на их алгебраические дополненияравна определителю.

• Сумма произведений всех элементов любого ряда на алгебраические дополнениясоответствующих элементов параллельного ряда равна нулю.

• Определитель произведения квадратных матриц одинакового порядка равен произведению их определителей (cм. также формулу Бине-Коши).

• С использованием индексной нотацииопределитель матрицы 3×3 может быть определён с помощьюсимвола Леви-Чивитаиз соотношения:

• 

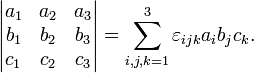
5.Для некоторых квадратных матриц можно найти так называемую обратную матрицу. Обратная матрица A ^{− 1} такова, что если умножить матрицу на неё, то получится единичная матрица:

• AA ^{− 1} = E

Теорема (о нахождении обратной матрицы). Пусть определитель матрицы не равен нулю, пусть матрица определяется выражением . Тогда при элементарном преобразовании строк матрицы к единичной матрице в составе одновременно происходит преобразование к .

Обратная матрица существует не всегда. Матрицы, для которых обратная существует, называются невырожденными(или регулярными), а для которых нет —вырожденными(или сингулярными). Матрица невырождена, если все ее строки (столбцы)линейно независимыкаквекторы.

Свойства обратной матрицы

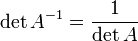• , где 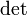обозначаетопределитель.

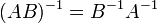• для любых двух обратимых матриц A и B.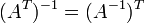

• где * ^T обозначает транспонированную матрицу.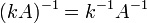

• для любого коэффициента .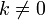

• Если необходимо решить систему линейных уравненийAx = b, (b — ненулевой вектор) где x — искомый вектор, и если A ^{− 1} существует, то x = A ^{− 1}b. В противном случае либо размерность пространстварешений больше нуля, либо их нет вовсе.

• 

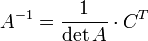
• C^T — транспонированная матрица алгебраических дополнений;

• 6, Рангом системы строк (столбцов) матрицыA с m строк и n столбцов называется максимальное число линейно независимыхстрок (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.

• Ранг матрицы — наивысший из порядков миноровэтой матрицы, отличных от нуля.

• Ранг матрицы — Размерность образа dim(im(A)) линейного оператора, которому соответствует матрица

• Пусть 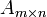— прямоугольная матрица.

• Тогда по определению рангом матрицы A является:

• ноль, если A — нулевая матрица;

• число 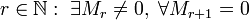, гдеM_r — минор матрицы A порядка r, а M_{r + 1} — окаймляющий к нему минор порядка (r + 1), если они существуют.

• Ранг 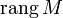матрицыM размера 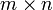называютполным, если .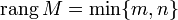

• Базисный минор матрицы A — любой ненулевой минорматрицыA порядка r, где .

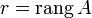  • Строки и столбцы, на пересечении которых стоит базисный минор, называются базисными строками и столбцами. (Они определены неоднозначно в силу неоднозначности базисного минора.)

• Существует несколько методов нахождения ранга матрицы:

• Метод элементарных преобразований

• Ранг матрицы равен числу ненулевых строк в матрице после приведения её к ступенчатой форме при помощи элементарных преобразований над строками матрицы.

• Метод окаймляющих миноров

• Пусть в матрице A найден ненулевой минор k-го порядка M. Рассмотрим все миноры (k + 1)-го порядка, включающие в себя (окаймляющие) минор M; если все они равны нулю, то ранг матрицы равен k. В противном случае среди окаймляющих миноров найдется ненулевой, и вся процедура повторяется.

• 7.Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решенийсистемы линейных алгебраических уравнений, которую представляет эта матрица.

• Элементарные преобразования используются в методе Гауссадля приведения матрицы ктреугольномуили ступенчатому виду.

• Определение

• Элементарными преобразованиями строк называют:

• перестановка местами любых двух строк матрицы;

• умножение любой строки матрицы на константу ,;

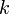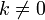• прибавление к любой строке матрицы другой строки, умноженной на константу ,.

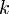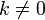• Элементарные преобразования обратимы.

• Обозначение 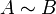указывает на то, что матрица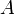может быть получена из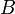путём элементарных преобразований (или наоборот).

Теорема (об инвариантности ранга при элементарных преобразованиях). Если , то .

8. Система m линейных уравненийсn неизвестными (или, линейная система) в линейной алгебре— это система уравнений вида

(1)

Здесь x₁, x₂, …, x_n — неизвестные, которые надо определить. a₁₁, a₁₂, …, a_mn — коэффициенты системы — и b₁, b₂, … b_m — свободные члены — предполагаются известными. Индексы коэффициентов (a_ij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно^[1].

Система (1) называется однородной, если все её свободные члены равны нулю (b₁ = b₂ = … = b_m = 0), иначе — неоднородной.

Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.

Решение системы (1) — совокупность n чисел c₁, c₂, …, c_n, таких что подстановка каждого c_i вместо x_i в систему (1) обращает все её уравнения в тождества.

Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.

Совместная система вида (1) может иметь одно или более решений.

Решения c₁⁽¹⁾, c₂⁽¹⁾, …, c_n⁽¹⁾ и c₁⁽²⁾, c₂⁽²⁾, …, c_n⁽²⁾ совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:

c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).

Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.

9. Система линейных уравнений может быть представлена в матричной форме как:

или: Ax = B.

Если к матрице А приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.

10. Метод обратной матрицы (Матричный метод) решения систем линейных алгебраических уравнений с ненулевым определителем основной матрицы состоит в поиске матрицы, обратной к основной матрице, и умножению ее на матрицу свободных членов.

Пусть дана система линейных уравнений с n неизвестными (над произвольным полем):

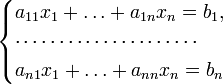
Тогда её можно переписать в матричной форме:

AX = B, где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:

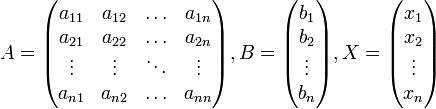
Умножим это матричное уравнение слева на A ^{− 1} — матрицу, обратную к матрице A: 

Так как A ^{− 1}A = E, получаем X = A ^{− 1}B. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) являетсяневырожденностьматрицы A. Необходимым и достаточным условием этого является неравенство нулюопределителя матрицыA:

.

Для однородной системы линейных уравнений, то есть когда вектор B = 0, действительно обратное правило: система AX = 0 имеет нетривиальное (то есть ненулевое) решение только если det A = 0. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит названиеальтернативы Фредгольма.

11. Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). Назван по имени Габриэля Крамера (1704–1752), придумавшего метод.

Решение:

Пример: