Бесконечно малая величина

Последовательность a_n называется бесконечно малой, если . Например, последовательность чисел  — бесконечно малая.

Функция называется бесконечно малой в окрестности точки x₀, если .

Функция называется бесконечно малой на бесконечности, если либо .

Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если , то f(x) − a = α(x), .

Бесконечно большая величина

Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция xsin x, неограниченная с обеих сторон, не является бесконечно большой при .

Последовательность a_n называется бесконечно большой, если .

Функция называется бесконечно большой в окрестности точки x₀, если .

Функция называется бесконечно большой на бесконечности, если либо .

Свойства бесконечно малых

• Сумма конечного числа бесконечно малых — бесконечно малая.

• Произведение бесконечно малых — бесконечно малая.

• Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.

• Если a_n — бесконечно малая последовательность, сохраняющая знак, то 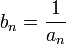— бесконечно большая последовательность.

24. Замеча́тельные преде́лы — термин, использующийся в советских и российских учебниках по математическому анализудля обозначения некоторых широко известныхматематических тождествсо взятиемпредела. Особенно известны:

• Первый замечательный предел:

• Второй замечательный предел:

Следствия

1. 

2. 

3. 

4. 

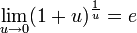
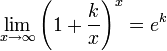
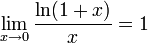
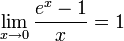
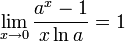5. для ,

6. 

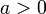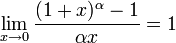
e — математическая константа, основание натурального логарифма, трансцендентное число. Иногда число e называют числомЭйлера или числом Непера. Обозначается строчной латинской буквой «e». Численное значение^[1]:

25.

Непрерывная функция — функция без «скачков», то есть такая у которой малые изменения аргументаприводят к малымизменениямзначения отображения. График непрерывной функции может быть начерчен «не отрывая карандаш от бумаги».

Непрерывная функция вообще говоря, — синоним понятия непрерывное отображение, тем не менее, чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, навещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающих вещественные значения.

Определение. Функция имеетточку разрыва при , если она определена слева и справа от точки, но в точкене выполняется хотя бы одно из условий непрерывности.

Точки разрыва функции :

1. Точка устранимого разрыва;

2. Точка разрыва первого рода;

3. Точка разрыва второго рода.

Точка являетсяточкой устранимого разрыва, если функция в точке не определена и существуют равные конечные пределыи, т.е..

Точка являетсяточкой разрыва первого рода, если существуют конечные пределыи, т.е. выполняется второе условие непрерывности и не выполняются остальные условия или хотя бы одно из них.

Точка являетсяточкой разрыва второго рода, если один из пределов иравен бесконечности ().

26. Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием. Обратный процесс — интегрирование.