
Тангенс угла наклона касательной прямой
Функция fl называется
касательной к f в
точке x0. Число ![]() является
угловым коэффициентом
или тангенсом угла наклонакасательной
прямой.
является
угловым коэффициентом
или тангенсом угла наклонакасательной
прямой.
Скорость изменения функции
Вообще производная функции y = f(x) в точке x0 выражает скорость изменения функции в точке x0, то есть скорость протеканияпроцесса, описанного зависимостью y = f(x).
27. Дифференци́руемая фу́нкция — это функция, имеющая дифференциал. Дифференцируемая функция может быть хорошо приближена линейной функцией. Дифференцируемость является одним из фундаментальных понятий в математике и имеет большое число приложений как внутри неё, так и в естественных науках, широко использующих математический аппарат (на данном отрезке).
Непрерывная функция — функция без «скачков», то есть такая у которой малые изменения аргументаприводят к малымизменениямзначения отображения. График непрерывной функции может быть начерчен «не отрывая карандаш от бумаги».
Ответ на первый вопрос: из непрерывности функции не следует ее дифференцируемость.
Ответ на второй вопрос: из дифференцируемости функции следует ее непрерывность.
Рассмотрим более конкретно каждый вопрос. Чтобы ответить на данные вопросы необходимо доказать озвученый факт или привести пример, который опровергает этот факт.
Найдем
производную следующей функции ![]() .
Хорошо известно, данная функция является
непрерывной и, что ее производная будет
следующей:
.
Хорошо известно, данная функция является
непрерывной и, что ее производная будет
следующей:

Покажем, что в точке нуль производная не существут. Для этого найдем производную в нуле по определению производной:
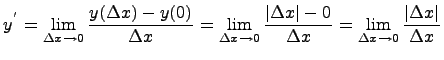
данный
предел равен 1, если ![]() и
равен (-1), если
и
равен (-1), если![]() ,
получаем, что предел не существует,
следовательно в нуле производной нет
и функция в нуле не дифференцируема.
,
получаем, что предел не существует,
следовательно в нуле производной нет
и функция в нуле не дифференцируема.
28
. C' = 0
x' = 1
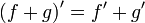 [2]
[2]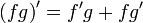 [3]
[3]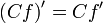
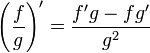 …(g ≠ 0)
…(g ≠ 0) (g ≠ 0)
(g ≠ 0)Если функция задана параметрически:
![]() ,
то
,
то ![]()
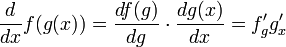
Формулы производной произведения и отношения обобщаются на случай n-кратного дифференцирования (формула Лейбница):
![]() где
где ![]() —биномиальные
коэффициенты.
—биномиальные
коэффициенты.
Следующие свойства производной служат дополнением к правилам дифференцирования:
если функция дифференцируема на интервале (a,b), то она непрерывна на интервале (a,b). Обратное, вообще говоря, неверно (например, функция y(x) = | x | на [ − 1,1]);
если функция имеет локальный максимум/минимум при значении аргумента, равном x, то f'(x) = 0 (это так называемая лемма Ферма);
производная данной функции единственна, но у разных функций могут быть одинаковые производные.
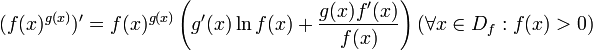
|
Функция
|
Производная
|
|
31. Дифференциа́л (от лат. differentia — разность, различие) — линейная часть приращения функции.
Обычно дифференциал функции f обозначается df. Некоторые авторы предпочитают обозначать df шрифтом прямого начертания, желая подчеркнуть, что дифференциал является оператором.
Матрица линейного оператора
 равнаматрице
Якоби;
её элементами являются частные
производные f.
равнаматрице
Якоби;
её элементами являются частные
производные f.Отметим, частные производные могут быть определены в точке, где дифференциал не определён.
Дифференциал функции f связан с её градиентом
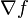 следущим
определяющим соотношением
следущим
определяющим соотношением
![]()
Дифференциал функции f связан с производной по направлению следущим определяющим соотношением
![]()
Термин «дифференциал» введён Лейбницем. Изначально dx применялось для обозначения «бесконечно малой» — величины, которая меньше всякой конечной величины и всё же не равна нулю. Подобный взгляд оказался неудобным в большинстве разделов математики за исключением нестандартного анализа.
геометрический смысл дифференциала. Возьмем на графике функции y = f(x) произвольную точку M(x,y) (рис21.). Проведем касательную к кривой y = f(x) в точке M, которая образует угол с положительным направлением оси OX, то есть f'(x) = tg . Из прямоугольного треугольника MKN
KN = MNtg xtg = f'(x) x,
то есть dy = KN.
Таким образом, дифференциал функции есть приращение ординаты касательной, проведенной к графику функции y = f(x) в данной точке, когда x получает приращение x.
Отметим основные свойства дифференциала, которые аналогичны свойствам производной.
d c = 0;
d(c u(x)) = c d u(x);
d(u(x) v(x)) = d u(x) d v(x);
d(u(x) v(x)) = v(x) d u(x) + u(x)d v(x);
d(u(x) / v(x)) = (v(x) d u(x) - u(x) d v(x)) / v2(x).
|
(5) |
Последнее равенство означает, что формула дифференциала не изменяется, если вместо функции от x рассматривать функцию от переменной u. Это свойство дифференциала получило название инвариантности формы первого дифференциала.
