
32. Производные высших порядков
Понятие производной произвольного порядка задаётся рекуррентно. Полагаем
![]()
Если функция f дифференцируема в x0, то производная первого порядка определяется соотношением
![]()
Пусть теперь производная n-го порядка f(n) определена в некоторой окрестности точки x0 и дифференцируема. Тогда
![]()
Если
функция ![]() имеет
в некоторой области D частную
производную по
одной из переменных, то названная
производная, сама являясь функцией
от
имеет
в некоторой области D частную
производную по
одной из переменных, то названная
производная, сама являясь функцией
от ![]() может иметь в некоторой точке
может иметь в некоторой точке ![]() частные
производные по той же или по любой другой
переменной. Для исходной функции
частные
производные по той же или по любой другой
переменной. Для исходной функции ![]() эти
производные будут частными производными
второго порядка (или вторыми частными
производными).
эти
производные будут частными производными
второго порядка (или вторыми частными
производными).
![]() или
или
![]()
![]() или
или
![]()
Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Например,
![]()
33. Дифференциал от дифференциала данной функции y=f(x) называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d2y: d(dy)=d2y.
Найдем выражение второго дифференциала. Т.к. dx от x не зависит, то при нахождении производной его можно считать постоянным, поэтому
d2y = d(dy) = d[f '(x)dx)] = [f '(x)dx]'dx = f ''(x)dx·dx = f ''(x)(dx)2.
Принято записывать (dx)2 = dx2. Итак, d2у= f''(x)dx2.
Аналогично третьим дифференциалом или дифференциалом третьего порядка функции называется дифференциал от ее второго дифференциала:
d3y=d(d2y)=[f ''(x)dx2]'dx=f '''(x)dx3.
Вообще дифференциалом n-го порядка называется первый дифференциал от дифференциала (n – 1)-го порядка: dn(y)=d(dn-1y)
|
dny = f (n)(x)dxn |
Отсюда, пользуясь дифференциалами различных порядков, производную любого порядка можно представить как отношение дифференциалов соответствующего порядка:
![]()
34.
Правило Бернулли[1]-Лопита́ля —
метод нахождения пределов
функций, раскрывающий
неопределённости вида 0
/ 0 и ![]() .
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций равен
пределу отношения их производных.
.
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций равен
пределу отношения их производных.
Условия:
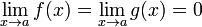 или
или 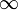 ;
;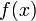 и
и 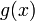 дифференцируемы
в проколотой окрестности
дифференцируемы
в проколотой окрестности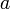 ;
;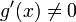 в
проколотой окрестности
в
проколотой окрестности 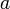 ;
;существует
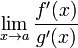 ,
,
тогда
существует ![]() .
.
Пределы также могут быть односторонними.
