12. Эквивалентность слау при элементарных преобразованиях

Назовём элементарными преобразованиями над системой линейных алгебраических уравнений:

• перестановку уравнений;

• умножение уравнения на ненулевую константу;

• сложение одного уравнения с другим, умноженным на некоторую константу.

Т.е. элементарные преобразования над её расширенной матрицей. Тогда справедливо следующее утверждение:

Напомним, что две системы называются эквивалентными, если множества их решений совпадают.

Теорема (об эквивалентности систем уравнений при элементарных преобразованиях). Система линейных алгебраических уравнений, полученная путём элементарных преобразований над исходной системой, эквивалентна ей.

13. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

• Количество главных переменных системыравно рангу системы.

• Совместная системабудет определена (её решение единственно), если ранг системы равен числу всех её переменных.

Теорема (об общем решении неоднородных систем). Пусть (т.е. система (2) совместна), тогда:

• если , где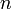— число переменных системы (2), то решение (2) существует и оно единственно;

• если 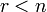, то общее решение системы (2) имеет вид, где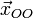— общее решение системы (1), называемоеобщим однородным решением, — частное решение системы (2), называемоечастным неоднородным решением.

14. Ме́тод Га́усса^[1] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключенияпеременных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные^[2].

Матрица A называется основной матрицей системы, b — столбцом свободных членов.

Тогда согласно свойству элементарных преобразованийнад строками основную матрицу этой системы можно привести к ступенчатому виду(эти же преобразования нужно применять к столбцу свободных членов):

При этом будем считать, что базисный минор(ненулевойминормаксимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных^[3].

Тогда переменные называютсяглавными переменными. Все остальные называются свободными.

Если хотя бы одно число , гдеi > r, то рассматриваемая система несовместна.

Пусть для любыхi > r.

Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом (, где— номер строки):

Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путёмэлементарных преобразованийнад исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.

Следствия: 1: Если в совместной системе все переменные главные, то такая система является определённой.

2: Если количество переменных в системе превосходит число уравнений, то такая система является либо неопределённой, либо несовместной

Метод Гаусса — Жордана (метод полного исключения неизвестных) — метод, который используется для решения квадратных систем линейных алгебраических уравнений, нахождения обратной матрицы, нахождения координат вектора в заданном базисе или отыскания ранга матрицы. Метод является модификацией метода Гаусса. Назван в честь К. Ф. Гаусса и немецкого геодезиста и математика Вильгельма Йордана^[1].

Алгоритм

1. Выбирают первый слева столбец матрицы, в котором есть хоть одно отличное от нуля значение.

2. Если самое верхнее число в этом столбце есть ноль, то меняют всю первую строку матрицыс другой строкой матрицы, где в этой колонке нет нуля.

3. Все элементы первой строки делят на верхний элемент выбранного столбца.

4. Из оставшихся строк вычитают первую строку, умноженную на первый элемент соответствующей строки, с целью получить первым элементом каждой строки (кроме первой) ноль.

5. Далее проводят такую же процедуру с матрицей, получающейся из исходной матрицы после вычёркивания первой строки и первого столбца.

6. После повторения этой процедуры n − 1 раз получают верхнюю треугольную матрицу

7. Вычитаем из предпоследней строки последнюю строку, умноженную на соответствующий коэффициент, с тем, чтобы в предпоследней строке осталась только 1 на главной диагонали.

8. Повторяют предыдущий шаг для последующих строк. В итоге получают единичную матрицу и решение на месте свободного вектора (с ним необходимо проводить все те же преобразования).

9. Чтобы получить обратную матрицу, нужно применить все операции в том же порядке к единичной матрице.

15. Однородной системой линейных уравнений называется система вида:

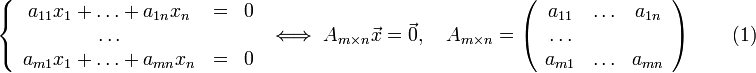
Нулевое решение системы (1) называетсятривиальным решением.

Однородные системы всегда совместны, т.к. всегда существует тривиальное решение.

Если существует любое ненулевое решение системы, то оно называется нетривиальным.

Решения однородной системы обладают свойством линейности:

16. НАТУРАЛЬНЫЕ (множество натуральных чисел обозначается N)

ЦЕЛЫЕ (множество целых обозначается Z)

РАЦИОНАЛЬНЫЕ (множество рациональных чисел обозначается R)

ИРРАЦИОНАЛЬНЫЕ (множество иррациональных обозначается I)

ДЕЙСТВИТЕЛЬНЫЕ (это множество получено объединением РАЦИОНАЛЬНЫХ и ИРРАЦИОНАЛЬНЫХ чисел, обозначается D)

КОМПЛЕКСНЫЕ числа, содержащие в себе мнимую единицу і, которая является квадратным корнем из –1.

17. Функцией f , действующей из множества X в множество Y (f: X Y) называется правило или закон, по которому каждому элементу x  X ставится в соответствие один или несколько y  Y. Если каждому x ставится в соответствие один y , то функция называется однозначно

Часто под термином «функция» понимается числовая функция; то есть функция которая ставит одни числа в соответствие другим. Эти функции удобно представляются на рисунках в виде графиков

Таким образом, функция — это упорядоченная тройка (или кортеж) объектов(f,X,Y), где

• множество X называется о́бластью определе́ния;

• множество Y называется о́бластью значе́ний;

• множество упорядоченных пар 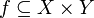или, что то же самое,график функции.

Способы задания функции

1.     Табличный.

2.     Графический 

3. Аналитический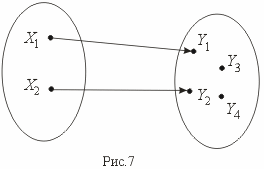

Отображение называется инъекцией, если для любых элементов x₁, x₂  X, для которых f(x₁) = f(x₂) следует, что x₁ = x₂. (рис. 7)

Сюръекцией (или отображением "на" ) называется отображение, при котором f(X) = Y (рис. 8).

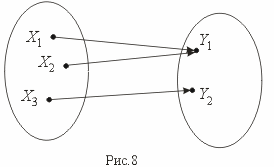
Биекция – это одновременно и сюръекция и инъекция (рис.9).

18. Элементарные функции

 Основными элементарными функциями называются следующие, аналитическим способом заданные функции.

 1. Степенная функция: , где  - действительное число*).

 2. Показательная функция: , где а - положительное число, не равное единице.

 3. Логарифмическая функция: , где основание лога­рифмов а - положительное число, не равное единице.

 4. Тригонометрические, функции:

 

 

 5. Обратные тригонометрические функции:

 y = arcsin x, y = arccos x, y = asctg x,

 y = arcctg x, y = arcsec x, y = arccosec x.

Обл.опр Степенная функция, .

 1.  - целое положительное число. Функция определена в бес­конечном интервале .

2.  - целое отрицательное число. В этом случае функция опре­делена при всех значениях х, кроме х = 0. 

 Показательная функция,  Эта функция определена при всех значениях х.

 Логарифмическая функция,  и  Эта функция определена при х > 0.

Тригонометрические функции. Не­зависимая переменная х в формулах y = sin x и т. д. выражается в радианасх. Все перечисленные тригонометрические функции периодически

19. Абсолю́тная величина́ или мо́дуль, обозначается . В случаевещественногоаргумента — непрерывнаякусочно-линейная функция, определённая следующим образом:

С геометрической точки зрения, модуль вещественного или комплексного числа есть расстояние между числом и началом координат. В математике широко используется тот факт, что геометрически величина означает расстояние между точками и и, таким образом, может быть использована как мера близости одной (вещественной или комплексной) величины к другой.

Для любых имеют место следующие соотношения:

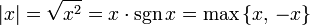• (см. Функция sgn(x)).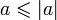

• 

• .

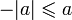Как для вещественных, так и для комплексных имеют место соотношения:

• , причём | a | = 0 тогда и только тогда, когда .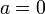

• | − a | = | a | .

• .

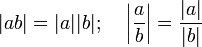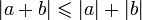• (неравенство треугольника).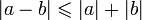

• .

• .

• .

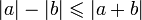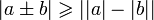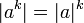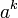• , если существует.

20. Моното́нная фу́нкция — это функция, приращениекоторой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное. Если в дополнение приращение не равно нулю, то функция называетсястро́го моното́нной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.

Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции.

 Периодическая функция

Периоди́ческая фу́нкция ― функция, повторяющая свои значения через какой-то ненулевой период, то есть не меняющая своего значения при добавлении к аргументу фиксированного ненулевого числа (периода).

Все тригонометрические функции являются периодическими

Функция называется периодической спери́одом , если справедливо

.

Если это равенствоне выполнено ни для какого, то функцияf называется апериоди́ческой.

Нечётные и чётные функции

• Функция 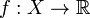называется нечётной, если справедливоравенство

• Функция f называется чётной, если справедливо равенство

Нечётные и чётные функции — функции, графики которых обладаютсимметриейотносительно изменения знака аргумента. Это понятие важно во многих областяхматематического анализа, таких как теориястепенных рядовирядов Фурье. Такое название возникло как обобщение чётности степенных функций: функцияf(x) = xⁿ чётна тогда и только тогда, когда n чётно, и нечётна тогда и только тогда, когда n нечётно.

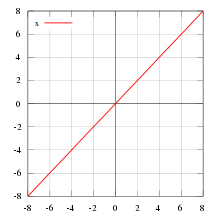
x) = x — пример нечётной функции.

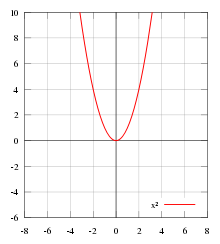
f(x) = x² — пример чётной функции.

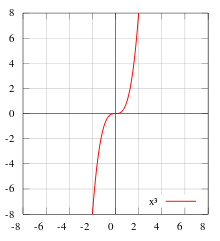
f(x) = x³, нечётная

f(x) = x³ + 1 ни чётная, ни нечётная

(

Другие определения:

• Нечётная функция — функция, меняющая знак при изменении знака независимого переменного (симметричнаяотносительно центра координат).

• Чётная функция — функция, не изменяющая своего значения при изменении знака независимого переменного (симметричнаяотносительно оси ординат).

• Индеферентная функция — функция, не обладающая симметрией. В эту категорию относят функции не подпадающие под предыдущие 2 категории

Ограниченная функция. Пусть функция (одного или многих переменных) определена на множестве D. Если множество ее значений ограничено, когда аргумент (аргументы) пробегают все множество D, функция называется ограниченной. Соответственно, если множество значений функции ограничено сверху (снизу), то функция также называется ограниченной сверху (снизу).

Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией.

Функция является обратной к функции, если выполнены следующие тождества:

• f(g(y)) = y для всех 

• g(f(x)) = x для всех 

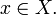
21. Предел

Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.

Функция имеет предел в точке , предельной для области определения функции , если для каждой окрестности предела существует проколотая окрестность точки , образ которой при отображении является подмножеством заданной окрестности точки .

Односторонний предел числовой функции в точке — это специфический предел, подразумевающий, что аргумент функции приближается к указанной точке с определённой стороны (слева или справа). Числовая функция имеет предел в точке тогда и только тогда, когда она имеет в этой точке совпадающие левый и правый пределы.

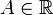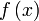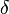• Число называетсяправосторонним пределом (правым пределом, пределом справа) функции в точке, если для всякого положительного числаотыщется отвечающее ему положительное числотакое, что для всех точек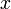изинтервала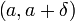справедливонеравенство.

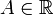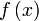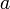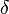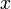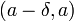• Число называетсялевосторонним пределом (левым пределом, пределом слева) функции в точке, если для всякого положительного числаотыщется отвечающее ему положительное числотакое, что для всех точекиз интерваласправедливо неравенство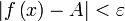.^[1]

Свойства Одна и та же функция в одной и той же точке может иметь только один предел.

• Сходящаяся функция локально сохраняет знак. Более обще,

где — проколотая окрестность точкиa.

• В частности, функция, сходящаяся к положительному (отрицательному) пределу, остаётся положительной (отрицательной) в некоторой окрестности предельной точки:

• Сходящаяся функция локально ограничена в окрестности предельной точки:

• Отделимость от нуля функций, имеющих предел, отличный от нуля.

• Операция взятия предела сохраняет нестрогие неравенства.

• Правило двух милиционеров

• Предел суммы равен сумме пределов:

• Предел разности равен разности пределов:

• Предел произведения равен произведению пределов:

• Предел частного равен частному пределов.

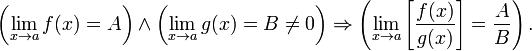
22.

Числовая последовательность — это последовательностьэлементов числового пространства.

Числовые последовательности являются одним из основных объектов рассмотрения в математическом анализе.

Пусть множество X — это либо множество вещественных чисел , либо множество комплексных чисел . Тогда последовательность элементов множества X называется числовой последовательностью. Предел последовательности — это объект, к которому члены последовательности приближаются с ростом номера. Так в произвольномтопологическом пространствепределом последовательности называется элемент, в любойокрестностикоторого лежат все члены последовательности, начиная с некоторого. В частности для числовых последовательностей предел — это число, в любой окрестности которого лежат все члены последовательности начиная с некоторого.

Частичный предел последовательности — это предел одной из её подпоследовательностей. У сходящихся числовых последовательностей он всегда совпадает с обычным пределом.

Верхний предел последовательности — это наибольшая предельная точка этой последовательности.

Нижний предел последовательности — это наименьшая предельная точка этой последовательности.

23. Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.

Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечностиопределённого знака.

Исчисление бесконечно малых — вычисления, производимые с бесконечно малыми величинами, при которых производный результат рассматривается как бесконечная сумма бесконечно малых. Исчисление бесконечно малых величин является общим понятием для дифференциальных и интегральных исчислений, составляющих основу современной высшей математики. Понятие бесконечно малой величины тесно связано с понятием предела.