
- •1.Матрицы и операции над ними.
- •2.Определители и их свойства.
- •3.Ранг матрицы.
- •4.Обратная матрица
- •5.Решение систем линейных алгебраических уравнений по формуле крамера.
- •6.Решение систем линейных алгебраических уравнений матричным методом.
- •8.Линейные операции над векторами.
- •10.Скалярное произведение вектора.
- •11. Векторное произведение векторов
- •12. Смешанное произведение векторов.
- •13. Понятие о линейном векторном пространстве
- •14. Базис. Собственные числа. Собственные вектора.
- •15. Простейшие задачи на плоскости (деление отрезка в заданном соотношении, расстояние между двумя точками).
- •16. Прямая на плоскости. Расстояние от точки до прямой. Угол между прямыми.
- •19. Прямая в пространстве, канонические уравнения
- •20. Элементы теории множеств
- •1. Логические символы
- •2. Операции над множествами
- •21. Функция, область определения, способы задания. Сложная и обратная функции
- •22. Предел функции
- •23. Основные теоремы о пределах
- •24. Замечательные пределы
- •1. Пусть . Каждое значение X заключено между двумя положительными целыми числами:, где— это целая часть X.
- •2. Пусть . Сделаем подстановку, тогда
- •25. Бесконечно малые и бесконечно большие функции и их свойства
- •28. Производная и дифференциал функции одной переменной.
- •30. Правила вычисления производных (диффиринцирования).
- •31. Таблица производных.
- •32.Производная сложных и обратных функций.
- •Геометрический смысл дифференциала
- •36. (Правило Лопиталя).
- •39. Понятие экстремума, основные теоремы.
- •Необходимое условие экстремума
- •Первое достаточное условие экстремума
- •Второе достаточное условие экстремума
- •40. Выпуклость и вогнутость, точки перегиба, асимптоты.
- •Теоремы о выпуклости функции и точках перегиба
- •41. Исследование функции и построение графика.
- •42. Наибольшее и наименьшее значение функции, непрерывной на отрезке.
- •44. Неопределенный интеграл, свойства.
- •45. Таблица интегралов
- •46. Основные методы интегрирования.
- •Свойства
- •49. Замена переменной, интегрирование по частям.
19. Прямая в пространстве, канонические уравнения
Если
известна некоторая точка пространства ![]() ,
принадлежащая прямой, и направляющий
вектор
,
принадлежащая прямой, и направляющий
вектор![]() данной
прямой, то канонические уравнения
этой прямой выражаются формулами:
данной
прямой, то канонические уравнения
этой прямой выражаются формулами:
![]()
Приведённая
запись предполагает, что координаты
направляющего вектора ![]() не
равны нулю.
Что делать, если одна или две координаты
нулевые, мы рассмотрим чуть позже.
не
равны нулю.
Что делать, если одна или две координаты
нулевые, мы рассмотрим чуть позже.
Пример 1
Составить
канонические уравнения прямой по
точке ![]() и
направляющему вектору
и
направляющему вектору![]()
Решение:
Канонические уравнения прямой составим
по формуле:
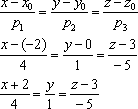
Ответ: ![]()
20. Элементы теории множеств
1. Логические символы
Квантор ![]() -
заменяет выражение "для любого",
"для произвольного", "для какого
бы ни было".
-
заменяет выражение "для любого",
"для произвольного", "для какого
бы ни было".
Квантор ![]() -
заменяет выражение "существует",
"найдется".
-
заменяет выражение "существует",
"найдется".
Запись ![]() (импликация)
означает, что из справедливости
высказыванияA вытекает
справедливость высказывания B.
Если, кроме того, из справедливости
высказывания B вытекает
справедливость A,
то записываем
(импликация)
означает, что из справедливости
высказыванияA вытекает
справедливость высказывания B.
Если, кроме того, из справедливости
высказывания B вытекает
справедливость A,
то записываем ![]() .
Если
.
Если![]() ,
то высказываниеB является
необходимым и достаточным условием
для того, чтобы выполнялось высказывание A.
,
то высказываниеB является
необходимым и достаточным условием
для того, чтобы выполнялось высказывание A.
Если
предложения A и B справедливы
одновременно, то записываем ![]() .
Если же справедливо хотя бы одно из
предложенийA илиB,
то записываем
.
Если же справедливо хотя бы одно из
предложенийA илиB,
то записываем ![]() .
.
2. Операции над множествами
Математическое понятие множества элементов принимается в качестве интуитивного. Множество задается правилом или признаком, согласно которому определяем, принадлежит ли данный элемент множеству или не принадлежит.
Множество обозначают символом A = {x}, где x - общее наименование элементов множества A. Часто множество записывают в видеA = {a, b, c, ...}, где в фигурных скобках указаны элементы множества A. Будем пользоваться обозначениями:
N - множество всех натуральных чисел; Z - множество всех целых чисел; Q - множество всех рациональных чисел; R - множество всех действительных чисел; C - множество всех комплексных чисел; Z0 - множество всех неотрицательных целых чисел.
Запись ![]() (или
(или![]() )
означает, что элементa принадлежит
множеству A.
)
означает, что элементa принадлежит
множеству A.
Запись ![]() (или
(или![]() )
означает, что элементa не
принадлежит множеству A.
)
означает, что элементa не
принадлежит множеству A.
21. Функция, область определения, способы задания. Сложная и обратная функции
Определение. Переменная величина y называется функцией переменной x (обозначается ), если каждому значению x соответствует определенное значение - число y.
Совокупность значений независимой переменной x, для которых определяются значения зависимой переменной y (т.е. значения функции y = f(x)) называется областью определения функции (или областью существования функции) и обозначается - Д.
Совокупность
значений y, соответствующих всем
значениям ![]() ,
называется областью изменения функции
и обозначается - Е.
,
называется областью изменения функции
и обозначается - Е.
Функция может быть задана различными способами.
1. Табличный способ задания функции заключается в составлении таблицы
в которой заданным значениям независимой переменной x ставятся в соответствие определенные значения функции y.
2. Графический Функция задается в виде графика (рис. 2).
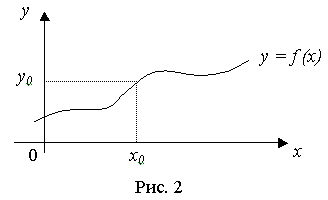
3. Аналитический способ. Функция задается в виде формулы, например:
![]()
Функция называется элементарной, если она задана одной формулой посредством конечного числа операций: сложения, вычитания, умножения, деления и взятия функции от функции - над основными элементарными функциями.
Основными элементарными функциями называются:
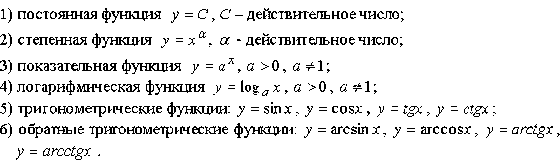
Пример
элементарной функции: ![]()
Пример
неэлементарной функции: 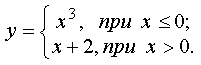
Определение. Пусть
область Д симметрична относительно
нуля. Функция f(x), ![]() ,
обладающая свойством: f(-x) = f(x) при
всех
,
обладающая свойством: f(-x) = f(x) при
всех![]() ,
называется четной функцией.
,
называется четной функцией.
Определение. Пусть
область Д симметрична относительно
нуля. Функция f(x), ![]() ,
обладающая свойством: f(-x) = - f(x) при
всех
,
обладающая свойством: f(-x) = - f(x) при
всех![]() ,
называется нечетной функцией.
,
называется нечетной функцией.
Например: функции y = x2, y = cosx - четные, а y = x3, y = sinx - нечетные.
Определение. Функция f(x) называется периодической с периодом T > 0, если существует число T > 0 такое, что y(x + T) = f(x) для всех
Например: y = sinx - периодическая функция с периодом T = 2π.
Определение. Пусть
функция z = φ (x) определена в некоторой
области Д, а функция y = f(x) определена
для всех x в области X, при этом все y =
f(x) лежат в области Д. Тогда переменная
z через посредство y и сама является
функцией от x: z = φ [f(x)], ![]() .
Полученная функция от функции называется
сложной функцией.
.
Полученная функция от функции называется
сложной функцией.
Пример. ![]() -
сложная функция, так как
-
сложная функция, так как ![]() где
U = sinx. При этом x таков, что
где
U = sinx. При этом x таков, что![]() (область
определения функции
(область
определения функции![]() )
)
