
attachment
.pdf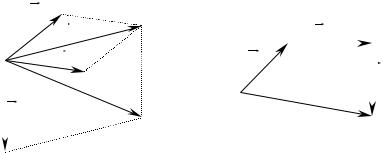
Правило паралелограма можна замінити правилом многокутника сил. Дійсно,
щоб знайти рівнодійну, потрібно знайти точку А (рис.2.4б) .Для цього з точки
A1 , кінця вектора F1 , потрібно провести вектор, геометрично рівний вектору
|
|
F2 . В точці |
A2 , кінця вектора F2 , будують вектор, геометрично рівний |
|
|
вектору F3 . |
|
З’єднавши початок першої сили (точку М) з кінцем останньої сили (точкою А),
отримаємо рівнодійну всіх трьох сил |
R як сторону, що замикає многокутник |
||||||
сил (рис.2.4б). |
|
|
|
|
|||
|
|
|
F1 |
|
|
|
|
|
|
|
F 1 2 |
А1 |
F 2 |
А2 |
|
М |
|
|
F 2 |
F1 |
|
|
F 3 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
R |
М |
|
|
|
|
|
F 3 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
R |
|
А |
|
|
|
|
А |
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
а) |
|
б) |
|
|
|
||
рис.2.4 |
|
|
|
|
|
||
Розглянемо часткову, але дуже важливу задачу про рівновагу матеріальної точки. Точка, яка знаходиться під дією системи сил і при цьому із прискоренням, рівним нулю, знаходиться у рівновазі.
Рівнодійна системи сил може бути представлена згідно із другим законом Ньютона
|
|
|
R mW . |
(b) |
|
Якщо при рівновазі точки її прискорення рівне нулю, то умовою
рівноваги точки являється рівність нулю рівнодійної
R = 0 . (2.4)
Механічна умова рівноваги системи сил , прикладених до точки.
Матеріальна точка знаходиться у рівновазі, якщо рівнодійна сил, прикладених до точки, рівна нулю.
Графічна умова рівноваги системи сил, прикладених до точки.
Матеріальна точка, на яку діє система сил, знаходиться у рівновазі, якщо многокутник сил, що діють на точку, є замкненим.
41

Для того щоб закінчити розглядати закони Ньютона, наведемо формулювання його третього закону, який зветься законом дії і протидії. Дією називається сила, що діє на точку, протидією – та сила, з якою точка діє на джерело першої сили. Дія і протидія завжди прикладені до різних точок або тіл.
Третій закон Ньютона (закон рівності дії і протидії).
Дія завжди рівна і прямо протилежна протидії.
Третій закон справедливий у будь-якій системі координат, бо він не містить кінематичних характеристик руху матеріальних об'єктів і дає змогу відрізнити реальні сили, прикладені до точок, від фіктивних, які можуть з'явитися при математичному розв'язанні задач механіки.
У перших двох законах Ньютона розглядається одна матеріальна точка , а у третьому законі - питання про взаємодію двох точок. Механічні взаємодії двох точок не зрівноважують один одне, бо вони прикладені до різних точок.
Для розв'язання задач статики необхідно ознайомитися з деякими аксіомами і теоремами механіки.
F |
A |
B |
F |
рис.2.5
Розглянемо абсолютно тверде тіло, до якого прикладені дві сили, рівні за величиною і направлені по одній прямій в протилежні напрямки (рис.2.5). Пряма, по якій направлена сила, називається її лінією дії.
Аксіома 2 (про абсолютно тверде тіло).
Якщо на абсолютно тверде тіло діють дві сили, рівні за величиною, направлені в протилежні сторони по загальній лінії дії, то ці дві сили зрівноважуються. Звідси випливає, що якщо абсолютно тверде тіло знаходиться у рівновазі під дією двох сил, то вони рівні за величиною, направлені у прямо протилежні сторони та мають спільну лінію дії.
Із аксіоми про абсолютно тверде тіло випливає наслідок: якщо зрівноважені системи сил прикласти до тіла або відкинути їх, то рух тіла при цьому не зміниться.
Усе сказане дозволяє довести теорему про абсолютно тверде тіло: сила, що прикладена до абсолютно твердого тіла може бути перенесена вздовж лінії її
дії.
Припустимо, що заданий вектор сили F , прикладеної в точці А. Доведемо, що
силу F можна перенести уздовж лінії дії в точку B (рис.2.6). Прикладемо в
точці В зрівноважену систему сил F і - F . Відкинемо силу F , прикладену в
точці А, і силу - F , прикладену в точці В, так як вони утворюють зрівноважену
систему сил. Після цього залишиться сила F , перенесена із точки А в точку В
42

уздовж лінії дії. Вектор сили, прикладеної до абсолютно твердого тіла, називається ковзаючим вектором. Вектор сили, прикладеної до матеріальної точки, переносити не можна. Тому він зветься визначним, або прикладеним вектором.
|
|
F |
F1 |
B |
|
|
|
|
|
|
F |
F |
3 |
O |
R |
|
|
|
|
|
F 2
A
F
рис.2.6 |
рис.2.7 |
Теорема про три сили.
Якщо тіло знаходиться у рівновазі під дією трьох непаралельних сил ( F1 , F2 ,
F3 ), з яких хоча б дві сили розташовані в одній площині, то лінії дії всіх сил перетинаються в одній точці.
Доведемо цю теорему.
|
|
|
|
|
|
Доведення. На тіло, яке знаходиться у рівновазі, діють три сили F1 , |
F2 , |
F3 |
|||
|
|
|
|
|
|
(рис.2.7). Тіло знаходиться у рівновазі, вектори F1 |
і F2 знаходяться в одній |
||||
|
|
|
|
|
|
площині. Продовжимо лінії дії сил F1 |
і F2 до їх перетину у точці О. Додамо |
||||
|
|
|
|
|
|
сили F1 |
і F2 за правилом паралелограма . Тоді на тіло діє дві сили: |
R і F3 . |
|||
На основі аксіоми про абсолютно тверде тіло можна стверджувати, що сили R і
F3 рівні за величиною, протилежні за напрямком і мають спільну лінію дії, тобто вони зрівноважуються. Теорему доведено.
Теорема про три сили дозволяє вирішувати прості задачі: якщо до тіла, яке знаходиться у рівновазі, прикладені три сили, із яких одна задана повністю, відомі лінія дії другої сили і точка прикладання третьої, то можна визначити величину і напрям усіх трьох сил, що діють на тіло.
2.1.2. Диференціальні рівняння руху вільної матеріальної точки
43

Диференціальні рівняння руху вільної матеріальної точки випливають із другого закону Ньютона, основного закону механіки. Із рівності, що виражає другий закон Ньютона
|
|
|
mW |
F , |
(a) |
можна отримати три види диференціальних рівнянь руху точки, що відповідають трьом способам задання руху точки.
Диференціальне рівняння руху точки у векторному вигляді
При векторному способі задання руху точки (рис.2.8) прискорення виражається формулою
|
|
|
|
|
|
d 2 r |
|
||
W |
|
. |
(b) |
|
dt2 |
||||
Другий закон Ньютона при цьому можна записати так:
|
d 2 |
|
|
|
|
|
r |
|
|||
т |
|
|
= F . |
(c) |
|
dt2 |
|||||
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
У частковому випадку вектор сили |
F |
|||
М |
|
може бути сталим за модулем і за напрямом. |
|||||
|
|
|
Якщо вектор сили змінюється, то він може |
||||
|
|
F |
залежати |
від |
багатьох |
змінних: від часу, |
від |
|
|
розташування |
точки в |
просторі, від радіус- |
|||
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
вектора |
r . |
Прикладом сил, залежних від |
||
r |
|
|
розташування |
точки, є сили всесвітнього |
|||
|
О |
|
тяжіння, |
електростатичні, магнітностатичні, |
|||
|
|
сили притягання і відштовхування. Сили опору |
|||||
рис.2.8 |
|
середовища, в якому відбувається рух, залежать |
|||||
|
від швидкості руху точки. Сили опору залежать |
||||||
|
|
|
|||||
|
|
|
|
|
|
|
|
також і від прискорення точки W . Залежність сил від прискорення тут розглядатись не буде, так як такого типу сили зустрічаються рідко (наприклад, в електродинаміці).
Рівняння (c) можна остаточно записати так
|
|
|
|
|
|
|
|
|
d 2 r |
d r |
|
|
|||
т |
|
|
= F t,r, |
|
|
(2.5) |
|
dt |
2 |
dt |
|||||
|
|
|
|
|
|
||
Диференціальні рівняння руху матеріальної точки у координатному
вигляді |
|
|
Припустимо, що на матеріальну точку М, |
що рухається |
діє система сил, |
|
|
|
рівнодійна яких рівна F (рис.2.9).Проекції |
сили F на |
осі координат |
позначимо X, Y, Z. Будемо користуватися прямокутною декартовою системою координат Oxyz. Положення точки на її траєкторії визначається у кожен момент часу координатами x, y, z.
44

Щоб |
скласти |
диференціальне |
z |
|
|
|
рівняння руху точки в координатному |
|
|
|
|||
вигляді, спроектуємо праву і ліву частини |
|
F |
|
|||
рівності (2.5) на осі координат. При цьому |
|
M |
|
|||
слід пам’ятати, що проекції вектора |
|
|
|
|||
швидкості |
точки на осі |
координат |
рівні |
O |
Z |
|
першим похідним, а проекції прискорення |
|
y |
||||
|
|
|||||
точки рівні другим похідним за часом від |
|
X |
|
|||
координат точки, що рухається. Отримаємо: |
Y |
|
||||
mx X(t, x, y,z, x, у, z), |
|
x |
|
|
||
my Y(t, x, y,z, x, у, z), |
(2.6) |
|
|
|
||
|
|
|
|
|
рис.2.9 |
|
mz Z(t, x, y,z, x, у, z), |
|
|
|
|||
|
|
|
|
|||
Невідомими функціями у (2.6) є координати точки як функції часу.
Диференціальні рівняння руху матеріальної точки у натуральному вигляді
Рівнодійна сил, що прикладаються до точки, так як і прискорення точки, лежить у стичній площині (рис.2.10). Проектуючи рівність (а) на осі натурального тригранника, отримаємо
mW F cosa ,
|
|
mWn Fsina . |
(d) |
|
|
||
|
|
V |
|||||
|
|
|
|
|
|
|
|
Замінив у рівняннях (d) W і Wn , знайдемо |
|
F |
|||||
т |
dV |
F cosa , т |
V 2 |
F sin . |
(2.7) |
|
|
dt |
|
|
|||||
|
|
|
|||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
рис.2.10 |
45

2.1.3. Дві основні задачі динаміки вільної матеріальної точки
Перша, або пряма, задача динаміки вільної матеріальної точки
Перша, або пряма, задача динаміки складається з наступного: кінетично заданий рух точки, відома маса точки. Необхідно знайти рівнодійну сил, прикладених до точки. Припустимо, що рух точки задано координатним способом
x=x(t), y=y(t), z=z(t) (a)
Щоб знайти рівнодійну сил, прикладених до точки, потрібно двічі продиференціювати за часом координати точки (а), помножити на масу і підставити в рівняння (2.6). Отримані таким способом проекції рівнодійної на осі координат повністю визначають вектор рівнодійної. Модуль рівнодійної
|
|
|
|
|
|
|
|
|
|
|
|
|
R = X 2+Y 2+Z2 |
|
|
(2.7) |
|||||
Напрям рівнодійної визначається напрямними косинусами: |
|
|||||||||
|
X |
|
|
|
|
Z |
|
|
||
cos( R,x)= |
; cos( R, y) = |
Y |
; |
cos( R,z) = |
; |
(2.8) |
||||
R |
|
R |
||||||||
|
|
|
R |
|
|
|
|
|||
Перша задача динаміки не представляє великих труднощів для розв'язання, так як вона зводиться до того, щоб двічі продиференціювати деякі функції.
Друга, або обернена, задача динаміки вільної матеріальної точки
Друга, або обернена, задача динаміки матеріальної точки складається з наступного: задані сили, що діють на точку, маса точки і початкові умови; знайти закон її руху.
Ця задача розв'язується інтегруванням диференціальних рівнянь руху точки. Для визначеності розглянемо диференціальні рівняння руху у координатній формі (2.6). Кожне з рівнянь системи (2.6) – диференціальне рівняння другого порядку. Загальний розв'язок системи (2.6) представимо відносно невідомих функцій x, y, z. У результаті інтегрування отримаємо координати x, y, z як функції часу і шести постійних інтегрування:
x = x(t,C1 ,C2 ,...,C6 ), |
|
y = y(t,C1 ,C2 ,...,C6 ), |
(2.9) |
z = z(t,C1 ,C2 ,...,C6 ).
Розв'язок системи (2.9) неповний, так як невідомі постійні інтегрування, які визначаються із початкових умов. Початковими умовами називають значення координат точки і проекції її швидкості, що відповідають певному
моменту часу t0 :
x0 , y0 , z0 , x0 , |
y0 , |
z0 |
при t t0 . |
(2.10) |
Шість початкових умов (2.10) дозволяють знайти шість постійних інтегрування. Для цього продиференціюємо за часом координати (2.9):
46
x = x(t,C1 ,C2 ,...,C6 ), |
|
|
y = y(t,C1 ,C2 ,...,C6 ), |
(2.11) |
|
|
|
|
z = z(t,C1 ,C2 ,...,C6 ).
Потім у системи рівнянь (2.9) і (2.11) підставимо початкові умови (2.10) та отримаємо шість алгебраїчних рівнянь, з яких знайдемо шість невідомих
C1 ,C2 ,...,C6 .
Підставивши значення постійних інтегрування у систему (2.9), знайдемо закон руху точки і остаточно розв'яжемо задачу.
Приклади розв’язання першої задачі динаміки. Умови рівноваги
В якості прикладу роглянемо рівновагу точки, при цьому прискорення точки дорівнює нулю. Вона може рухатись рівномірно і прямолінійно по відношенню до системи координат, що рухається поступально:
Wx x 0 ; Wy y 0; |
Wz z 0. |
(a) |
|
|
|
Якщо проекції прискорення на осі координат рівні нулю, то рівні нулю і проекції рівнодійної на осі координат
X=0; Y=0; Z=0; (b)
Рівнодійна рівна векторній сумі сил, прикладених до точки. Рівність нулю векторної суми зумовлює рівність нулю алгебраїчних сум проекцій складових сил:
n |
n |
n |
|
Yi = 0; |
Zi = 0. |
|
|
Xi = 0; |
(2.12) |
||
i=1 |
i=1 |
i=1 |
|
Три рівності (2.12) називаються рівняннями рівноваги точки. Вони містять невідомі проекції сил, які знаходять у результаті розв’язання задачі. Задача є визначеною, якщо число невідомих не більше трьох. Якщо кількість невідомих більше трьох, задача вважається статично невизначеною і методами теоретичної механіки розв’язана бути не може.
Аналітичні умови рівноваги матеріальної точки
Матеріальна точка знаходиться в рівновазі, якщо алгебраїчні суми проекцій сил, прикладених до точки на три координатні осі рівні нулю.
Якщо точка розташована у площині, для її рівноваги достатньо скласти два рівняння рівноваги, якщо рух по прямій, достатньо скласти одне рівняння.
47
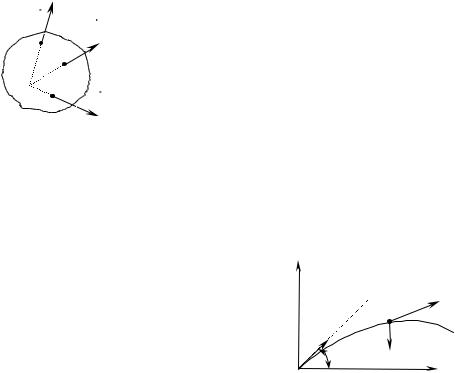
Рівновага тіла, що знаходиться під дією системи збіжних сил
Система сил називається збіжною, якщо лінії дії сил перетинаються в одній точці.
Припустимо, що до тіла прикладена збіжна система сил (рис.2.11). Вектори сил можна переносити уздовж лінії дії. Якщо всі сили перенести у точку перетину, знову отримаємо систему сил, прикладених до точки. Тому для
|
|
|
системи збіжних сил, діючих на тверде тіло, залишаються |
|||||||
F1 |
|
|
ті |
ж |
умови рівноваги |
(2.12) , |
що і для |
системи сил, |
||
|
F2 |
прикладених до точки. |
|
|
|
|||||
|
|
|
|
|
||||||
|
|
|
|
|
Ньютон розглянув частковий випадок першої |
|||||
|
|
|
задачі |
|
динаміки. Із |
законів |
Кеплера, |
встановлених |
||
O |
|
|
емпірично, йому були відомі закони руху планет навколо |
|||||||
|
|
Fn |
Сонця. |
Він поставив перед собою мету – знайти сили, під |
||||||
|
|
дією яких планети здійснюють рух. При розв'язанні цієї |
||||||||
рис.2.11 |
|
задачі Ньютон відкрив закон всесвітнього тяжіння. |
||||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
Приклад розв’язання другої задачі динаміки |
|
||||||
Розглянемо так звану задачу балістики. Із точки О у вакуумі вилітає |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
матеріальна точка маси m зі швидкістю V0 , що утворює із горизонтом кут |
||||||||||
(рис.2.12). Знайти закон руху точки. |
|
|
|
|
||||||
Розв’язання. |
|
|
|
|
|
|
|
|||
1) Оберемо спосіб задання руху |
|
|
|
|||||||
точки. Векторний |
спосіб |
задання |
руху |
y |
|
|
||||
застосовуютьо тільки при доведенні теорем. |
|
|
||||||||
|
|
|||||||||
Натуральний |
спосіб |
задання |
руху |
|
|
V |
||||
використовують лише у тому випадку, коли |
|
M |
||||||||
відома траєкторія точки. В нашій задачі |
|
|
|
|||||||
необхідно |
знайти |
траєкторію точки, тому |
V0 |
|
mg |
|||||
натуральний |
спосіб |
завдання |
руху |
|
|
|||||
O |
|
|
||||||||
застосувати |
не |
можна. |
Обираємо |
|
x |
|||||
|
|
|||||||||
координатний спосіб задання руху. Початок |
|
|
||||||||
|
рис.2.12 |
|||||||||
координат розташуємо у точці О, вісь Ox |
|
|||||||||
направимо горизонтально, вісь Oy – |
|
|
|
|||||||
вертикально вгору. |
|
|
|
|
|
|
|
|
||
2) |
Проаналізуємо |
сили, які |
діють |
на точку. Розглянемо довільне |
||||||
|
|
|
|
|
|
|
|
|
|
|
положення точки М на траєкторії. |
На точку діє сила тяжіння |
m g . Силою |
||||||||
опору нехтуємо.
Якщо б на точку не діяла сила тяжіння, вона рухалась би по прямій, що
співпадає із напрямком V0 . Точка М рухається у площині Оxy, |
тому складемо |
||
два диференціальних рівняння руху |
; |
my = -mg . |
(а) |
mx = 0 |
|||
|
|
|
|
Спростимо рівняння (а):
48

x = 0 ; y = - g .
Інтегруємо рівняння (b) :
; y -gt C3
Інтегруючи ще раз, отримаємо :
gt2
x = C1t+C2 ; y = - 2 +C3t+C4 ;
Сталі інтегрування знайдемо із початкових умов руху:
при t=0 |
x0 V0 cos C1 , |
y0 V0 sin C3 , |
x0 0 C2 , y0 |
|
|
|
|
Тоді закон руху матеріальної точки матиме вигляд:
(b)
(с)
(d)
0 C4 .
x = V 0cos t ; |
y = - |
gt2 |
V 0sin t . |
|
2 |
||||
|
|
|
2.1.4. Вільні та невільні системи матеріальних точок. В'язі та їх реакції
Системою матеріальних точок називається сукупність матеріальних точок, положення і рух яких пов'язані між собою.
Всі тіла, які ми бачимо навколо себе можна розглядати, як системи матеріальних точок. Розрізняють вільні та невільні системи матеріальних точок.
Вільними називаються такі матеріальні об'єкти, на рух яких не накладені наперед задані обмеження. І навпаки.
В'язями називають тіла, які обмежують свободу руху точок матеріальної системи безпосереднім контактом з її точками.
Це визначення є нестрогим. Тому при характеристиці в'язі частіше за все звертаються до її аналітичного визначення. Кожну в'язь можна описати рівнянням.
Сила, з якою в'язь діє на матеріальний об'єкт називається реакцією в'язі і відноситься до сил пасивних, на відміну від сил активних або тих, що задаються.
|
Розглянемо деякі приклади. Поверхня, по якій |
|
||||||
|
рухається точка М, є для неї в'яззю (рис.2.13). Якщо |
|
||||||
М(x,y,z) |
рівняння поверхні можна представити у вигляді |
|
|
|||||
|
|
|
f(x, y, z)=0, (2.13) |
|
|
|||
|
|
|
|
|
|
|||
|
в'язь називається стаціонарною. В рівняння в'язі |
|
||||||
|
час явно не входить, поверхня нерухома. |
|
|
|||||
|
Якщо поверхня рухається, в рівняння поверхні |
|
||||||
рис.2.13 |
входить час |
|
|
|
|
f(t, x, y, z)=0, |
( |
|
в'язь називається нестаціонарною. |
|
|
||||||
|
|
|
||||||
Якщо в рівняння в'язі не входять проекції швидкостей точок системи, то |
|
|||||||
в'язь називається геометричною. Якщо ж в'язь задається рівнянням виду |
|
|
||||||
f(t,x1 |
,y1 ,z1 ,...,xn ,yn ,zn ,x1 |
,y1 |
,z1 |
,...,xn ,yn |
,zn )=0 , |
(2.15) |
|
|
|
|
|
|
|
|
|
|
|
49
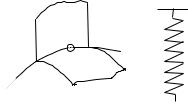
нестаціонарною кінематичною.
|
|
Як приклад в'язі можна розглянути |
|
|
дріт, по якому рухається кільце М (рис.2.14). |
M |
B |
Криву АВ можна розглядати як перетин двох |
|
поверхонь. В'язь АВ характеризується двома |
|
|
|
|
|
|
рівняннями: |
|
M |
|
|
f1(x,y,z)=0 , f2(x,y,z)=0 . |
(2.16) |
|
|
|
|
||||
|
|
|
Розглянемо рух точки М, прикріпленої |
|||
|
|
|
||||
рис.2.14 |
рис.2.15 |
|||||
до пружини (рис.2.15). Рух |
пружини |
|||||
залежить від закону руху точки М. В цьому випадку в'язь неможливо описати рівнянням руху точки М, тому її можна вважати вільною.
Повернемося до розгляду вільних систем матеріальних точок. Система матеріальних точок називається вільною, якщо на рух її точок не накладені наперед задані, тобто незалежні від закону руху обмеження. Прикладом вільної системи матеріальних точок є сонячна система, якщо комети, планети, Сонце розглядати як матеріальні точки. Таке уявлення про сонячну систему введено Ньютоном. Закони Ньютона справедливі лише для вільних матеріальних об'єктів.
Як про курйоз можна згадати про уявлення Птоломея про всесвіт, за яким центром всесвіту вважалася Земля, а Сонце, зірки та планети рухалися навколо Землі за допомоги системи коліс. Птоломей вважав сонячну систему невільною.
Система матеріальних точок називається невільною, якщо на рух точок системи накладені в'язі.
На земній поверхні спостерігається взаємодія тіл при їх русі. Тому всі тіла, які ми спостерігаємо навколо себе, є прикладом невільних систем. Виникає питання, як використати закони Ньютона, знайдені ним для вільних систем, для вивчення систем невільних? Різницю між вільними та невільними системами можна усунути, вводячи аксіому про звільнення від в'язей.
Аксіома 3 (про звільнення від в'язей).
Стан спокою матеріальної системи, або стан прямолінійного рівномірного руху не зміниться, якщо накладені на неї в'язі відкинути і замінити їх дію силами, що дорівнюють реакціям відкинутих в'язей.
Розглянемо балку АВ, яка знаходиться в стані рівноваги та розміщена на двох опорах. На балку діють сили Р1 та Р2 (рис.2.16). Рівновага балки не порушиться, якщо дію опор замінити електромагнітами, після чого її можна розглядати як вільну, використовуючи до неї закони Ньютона.
50
