
b
.pdfВ.Н. Иванов
ВАРИАЦИОННЫЕ ПРИНЦИПЫ И МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ТЕОРИИ УПРУГОСТИ
Допущено Министерством образования Российской Федерации
в качестве учебного пособия для студентов высших учебных заведений,
обучающихся по направлению «Строительство»
Москва Издательство Российского университета дружбы народов
2004
ББК 22.251.6 И 20
Утверждено РИС Ученого совета
Российского университета дружбы народов
Р е ц е н з е н т ы:
профессор, доктор физико-математических наук Б.Ф. Власов, профессор, доктор технических наук С.Я. Маковенко
Иванов В.Н.
И 20 Вариационные принципы и методы решения задач теории упругости: Учеб. пособие − М.: Изд-во РУДН, 2004. − 176 с.: ил.
ISBN 5 − 209 − 01172 − 0
В пособии дается краткое изложение элементов вариационного исчисления, на основе которых доказывается принцип Лагранжа. На базе принципа Лагранжа разработаны различные вариационные методы расчета строительных конструкций, используемых в инженерной практике и научных исследованиях. Рассматриваются вариационные методы решения задач теории упругости: метод Ритца−Тимошенко, метод Канторовича−Власова, а также метод Бубнова−Галеркина. Приводятся примеры расчета пластин и стержней вариационными методами.
Для студентов высших учебных заведений, обучающихся по направлению «Строительство». Пособие может быть рекомендовано студентам и аспирантам различных технических специальностей.
ISBN. 5 − 209 − 01172 − 0 |
ББК 22.251.6 |
©Издательство Российского университета дружбы народов, 2004 г.
©В.Н.Иванов, 2004 г.
ВВЕДЕНИЕ
Пространственная задача теории упругости описывается системой 15 уравнений с 15 неизвестными [1,4,5]. При решении задачи в напряжениях к трем уравнениям равновесия добавляется система 6 уравнений неразрывности деформаций. Общая система уравнений теории упругости может быть приведена к системе 3 дифференциальных уравнений в частных производных в перемещениях или к системе 6 дифференциальных уравнений в частных производных в напряжениях. Общий порядок системы дифференциальных уравнений в перемещениях - 9-й, системы уравнений в напряжениях - 12-й. Для конкретной задачи решение должно удовлетворять также граничным условиям в перемещениях или напряжениях или смешанным граничным условиям. В каждой точке поверхности тела при решении пространственной задачи удовлетворяется 3 граничных условия.
В декартовой прямоугольной системе координат получаем систему дифференциальных уравнений в частных производных с постоянными коэффициентами. Если используются криволинейные системы координат - цилиндрическая, сферическая, эллиптическая и другие, то получаем систему уравнений с коэффициентами, являющимися функциями координат. Применение криволинейных систем координат связано с формой рассматриваемых объектов - цилиндром, сферой, эллипсоидом и другими телами более сложных очертаний. Использование прямоугольной системы координат приводит в этом случае к усложнению формулировки граничных условий и их удовлетворению в процессе решения задачи.
Сложность системы уравнений, описывающих задачи теории упругости, не позволяет получить точного решения большинства задач. Точные решения известны лишь для ограниченного числа задач пространственной теории упругости.
Для решения ряда задач вводят гипотезы, понижающие порядок системы уравнений и позволяющие упростить процесс решения задачи - плоская задача теории упругости, теория изгиба тонких плит и оболочек, теория изгиба плит и оболочек средней толщины. Плоская задача теории упругости приводится к дифференциальному уравнению 4-го порядка в перемещениях или для функции напряжений. К разрешающему уравнению 4-го порядка приводится и задача изгиба тонких пластин. В теории тонких оболочек задача приводится к системе уравнений в частных производных 8-го порядка. Причем, за исключением цилиндрических и пологих оболочек, это система уравнений с переменными коэффициентами. И только для случая тел в виде стержней задача приводится к обыкновенному дифференциальному уравнению 4-го порядка и может быть решена в общем виде. Последний тип задач рассматривается в курсах сопротивления материалов и строительной механики стержневых систем.
О сложности задач теории упругости говорит тот факт, что в курсе математической физики, занимающейся теорией дифференциальных уравнений в частных производных, в основном рассматриваются дифференциальные уравнения 2-го порядка и лишь в некоторых курсах затрагиваются вопросы решения дифференциальных уравнений в частных производных 4- го порядка.
Для решения задач теории упругости часто приходится использовать различные численные и численно-аналитические
методы [6−9]. К численным методам относятся метод конечных разностей, метод конечных элементов, вариационно-разностный метод, метод граничных элементов и другие. К численноаналитическим методам автор относит методы, в которых решение может быть записано в аналитической форме, но неопределенные коэффициенты или функции могут быть определены в результате
реализации какого-то численного алгоритма. К таким методам относятся большинство вариационных методов: метод Ритца−Тимошенко, метод Канторовича - Власова, метод Трефца
[6,9−13] , а также метод Бубнова−Галеркина, метод коллокаций, численная реализация метода интегральных уравнений, метод потенциала [18,19] и другие.
Винженерной практике и научных исследованиях наиболее часто используются вариационные методы Ритца−Тимошенко и Канторовича−Власова, а также метод Бубнова−Галеркина, который не является вариационным, но этот термин часто к нему применяют. Из численных методов расчета наиболее используемым долгое время был метод конечных разностей (метод сеток) [14]. В последние три десятилетия он практически вытеснен методом конечных элементов - МКЭ [15-17] . В основе теории метода конечных элементов лежат вариационные принципы, что делает этот метод более гибким и более простым в реализации, чем метод конечных разностей, особенно при формулировке и удовлетворении граничных условий. Успешную конкуренцию этим методам может составить вариационно-разностный метод, который в настоящее время используется реже. В задачах для тел сложной формы и в случае наличия источников концентрации напряжений успешно применяется метод потенциала или метод интегральных граничных уравнений [18,19] и численный аналог этого метода - метод граничного элемента.
Вданном пособии рассматриваются вариационный принцип Лагранжа и методы решения задач теории упругости, основанные
на этом принципе, а также метод Бубнова−Галеркина, так как они наиболее широко используются в проектной практике и научных исследованиях.
Вариационные методы решения задач теории упругости, основаны на различных вариационных принципах, из которых наиболее известен принцип Лагранжа. Принцип Лагранжа известен студентам из курсов сопротивления материалов и строительной механики. Он используется при выводе интеграла Мора для определения перемещений стержневых систем, доказательства теоремы Бетти о взаимности работ, вывода системы канонических уравнений метода сил при расчете статически неопределимых стержневых систем.
Строгое доказательство принципа Лагранжа и других вариационных принципов теории упругости может быть проведено методами вариационного исчисления, специального раздела математики. Элементы вариационного исчисления излагаются в первой главе настоящего пособия. В пособии приводится минимум сведений из курса вариационного исчисления, необходимый для доказательства принципа Лагранжа и обоснования вариационных методов решения задач теории упругости. Более полно с методами и задачами вариационного исчисления можно ознакомиться в курсах [20-231.
I. ОСНОВЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
Вариационное исчисление является одной из старейших математических дисциплин. Оно развивалось почти одновременно с математическим анализом. Обычно основателями вариационного исчисления считают братьев Бернулли, Эйлера, Лагранжа. Вариационное исчисление примыкает к теории максимумов и минимумов математического анализа и является основой методов оптимального проектирования. В вариационном исчислении исследуются функционалы - объекты, более сложные, чем функции. Вариационное исчисление тесно связано с приложениями математики к механике, физике, инженерному делу, технике, численному анализу.

Приведем несколько примеров, которые дают представление о целях и задачах вариационного исчисления.
1. Задача о брахистохроне. Задача была сформулирована в 1696 году Иоганом Бернулли: отыскать кривую, двигаясь по которой под действием только силы тяжести (без трения)
материальная точка попадет из точки |
A в точку B, находящихся |
||||||||||||||||
в разных уровнях, в кратчайшее время (рис. 1.1). |
|||||||||||||||||
0 |
|
A |
|
|
|
|
|
|
|
|
|
На основании закона движения |
|||||
|
|
|
|
s(x,y) |
x |
|
|
|
твердого тела массой т под |
||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
• |
|
|
|
|
|
действием сила тяжести имеем: |
||||||
|
|
|
|
|
|
|
|
|
|
v = ds = |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2g y - скорость дви- |
|||||
|
|
|
|
|
|
|
v(x,y) |
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
y |
|
|
|
|
|
|
|
|
жения точки; у - расстояние по |
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
Рис. 1.1. К определению |
кривой |
|
|
вертикали; s(x,y) - длина дуги |
|||||||||||||
|
|
кривой движения точки; |
|||||||||||||||
|
|
наибыстрейшего спуска |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
ds = dx2 + dy 2 = 1 + y′2 dx ; |
|||||
y′ = |
dy |
; g - ускорение силы тяжести. |
|
|
|
|
|
||||||||||
dx |
|
|
|
|
|
||||||||||||
t |
l |
dt |
|
l |
ds = |
1 |
l |
|
1 |
|
1 |
l |
1 |
(1 + y′2 )dx . (1.1) |
|||
T = ∫dt = ∫ |
ds = ∫ |
∫ y |
− |
|
ds = |
∫ y |
− |
|
|||||||||
2 |
2 |
||||||||||||||||
0 |
0 |
ds |
0 |
v |
2g |
0 |
|
|
|
2g |
0 |
|
|
|
|||
Решение задачи о брахистохроне было дано И. Бернулли, Я. Бернулли, И. Ньютоном, Г. Лопиталем. Оказалось, что линией быстрейшего ската является циклоида.
2.Задача о геодезических кривых. Требуется определить линию наименьшей длины, соединяющую две точки.
Решение этой задачи в обычном трехмерном пространстве известно - кратчайшим расстоянием, соединяющим две точки, является прямая линия. Однако задача осложняется, если рассматривать точки какой либо поверхности. Эта задача рассматривается в курсе дифференциальной геометрии. Линии кратчайшего расстояния, соединяющие точки поверхности, называются геодезическими кривыми. Эта задача имеет важное прикладное значение в геодезии. Если рассматривать точки сферы, то линия кратчайшего расстояния между двумя точками является дугой окружности в плоскости, проходящей через заданные точки
ицентр сферы. Если рассматривать точки цилиндрической или конической поверхностей, то ответ о линии кратчайшего пути между двумя точками уже не является столь простым и очевидным.
3.Задача о минимальных поверхностях. Минимальной поверхностью называют поверхность минимальной площади, натянутую на заданный контур.
Сформулируем задачу о минимальной поверхности вращения
(рис. 1.2).
Площадь поверхности вращения определяется формулой
S = 2π x∫1 y(x)ds =2π x∫1 y(x) 1 + y′2 dx . |
(1.2) |
|
0 |
0 |
|
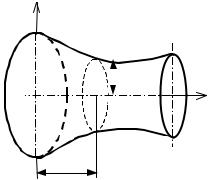
На |
практике |
|
у |
|||
минимальная |
поверхность |
|
||||
может быть |
получена с |
|
|
|
|
|
помощью мыльной пленки, |
|
|
|
|
|
|
натянутой на за-данный |
|
|
|
|
|
|
|
|
|
|
|
||
контур. |
Минимальные |
|
|
|
|
у(х) |
|
|
|
|
|||
поверхности |
могут |
0 |
|
|
|
х |
|
|
|
||||
использоваться |
для |
|
|
|
||
|
|
|
||||
оптимального |
|
|
|
|
|
|
проектирования |
|
|
|
|
|
|
пространственных |
|
х |
||||
оболочечных конструкций. |
|
|||||
4. Задача о наибольшей площади. Определить замкнутую кривую заданной длины, ограничивающую наибольшую площадь.
Решением данной задачи является окружность. Однако, задача осложнится, если часть кривой, ограничивающей искомую площадь является заданной незамкнутой кривой, к которой необходимо добавить искомую незамкнутую кривую заданной длины, сопряженную с заданной кривой.
Приведенные примеры позволяют получить представления о задачах, которыми занимается вариационное исчисление - из множества функций найти функцию - кривая движения тела, линия на поверхности, образующая поверхности вращения, площадь, ограничиваемая кривой линией, для которой достигается минимум (максимум) некоторого параметра - время движения, длина кривой, площадь поверхности или площадь внутри контура заданной длины.
1.1.Понятие о функционале. Линейный функционал. Вариация функционала.
Объекты, для которых ищется экстремальное значение в приведенных примерах, называются функционалами. Можно сказать, что функционалы являются функциями, аргументами которых являются функции из заданного класса функций.
Прежде чем дать окончательное определение функционала введем понятие класса функций - множество функций,
обладающих заданными свойствами, называется классом функций.
Чтобы задать класс функций достаточно перечислить свойства, которые налагаются на рассматриваемое множество функций. В курсах математики и приложениях рассматриваются некоторые классы функций, которые имеют общепринятые обозначения:
1.Класс непрерывных функций - С или С0.
2.Класс непрерывных функций с непрерывными первыми производными – C1.
3. Класс непрерывных функций с |
|
п |
|
непрерывными |
производными – Сn. |
|
|
|
|
4. Класс интегрируемых функций |
- |
L1 |
|
- множество |
функций, имеющих конечное значение определенного |
||||
интеграла в заданном интервале (а, b) |
- |
∫b |
f (x)dx ≤ A . |
|
a

5. Класс квадратично-интегрируемых функций – L2 -
множество функций, имеющих конечное значение определенного интеграла от квадрата функции, или произведения двух функций данного класса в заданном интервале (а, b) –
∫b |
f 2 (x)dx ≤ A или |
∫b |
f (x) ϕ(x)dx ≤ A |
a |
|
a |
|
Очевидно, класс непрерывных функций С включает в себя классы функций С1, С2, …, Сn. Класс функций С1 включает классы функций Сn при п > 1. Класс функций Ск включает классы функций Сn при п > к.
Вприложениях, в частности в вариационных методах теории
упругости важное место занимает класс функций L2 - проблема минимума квадратичного функционала.
Кроме перечисленных выше классов функций, могут рассматриваться классы кусочно-непрерывных или кусочнопостоянных функций, разрывных функций с конечным числом разрывов в рассматриваемом интервале и так далее.
Опираясь на понятие класса функций, введем определение функционала - говорят, что в классе функций задан функционал, если каждой функции рассматриваемого класса функций поставлено в соответствие число.
Вприведенных выше примерах функционалами являются: время движения тела между двумя точками; длина кривой между двумя точками поверхности; площадь поверхности вращения; площадь, ограниченная замкнутой кривой, и т.д. В механике функционалами являются потенциальная и кинетическая энергия твердых тел. В теории упругости важной характеристикой является энергия деформаций - функционал, характеризующий напряженно-деформированное состояние твердого деформируемого тела.
Будем далее функционал от функции у(х) обозначать J[y(x)]. Так для задачи о минимальной поверхности вращения (пример 3):
x |
|
J[y(x)]= S = ∫1 |
y( x ) 1 + y′2 (x)dx, y(x) C , |
0 |
|
где, у(х) С означает, что функция у(х) принадлежит классу С -
классу непрерывных функций, читается, как входит в (принадлежит).
Введем понятие линейного функционала. Функционал J[y(x)] называется линейным, если для любых функций у(х), у1(х), у2(х) из заданного класса функций:
a) J[c y(x)] = c J[y(x)], б) J[y1(x) + y2(x)] = J[y1(x)] + J[y2(x)],
или, обобщая случаи а и б, |
|
J[c1 y1(x) + c2 y2(x)] = c1 J[y1(x)] + c2 J[y2(x)]. |
(1.1.1) |
Основной задачей вариационного исчисления является задача об исследовании функционала на экстремум - из класса функций найти функцию, для которой исследуемый функционал достигает экстремального (наибольшего или наименьшего) значения.
Задача об исследовании функционала на экстремум во многом сходна с задачей нахождения экстремума функций. При исследовании функции на экстремум изучается ее поведение в окрестности точки, при малом изменении аргумента. При исследовании на экстремум функционала нужно анализировать поведение функционала при малых изменениях аргумента (функции), для которой вычисляется заданный функционал.
Приращением, вариацией δy аргумента у(х) функционала J[y(x)] называется разность между двумя функциями:
δ y(x)= y1 (x)− y(x). При этом предполагается, что у(х) |
меняется |
||
произвольно в некотором классе функций. |
|
||
Функционал J[y(x)] |
называется непрерывным, если малому |
||
изменению функции |
у(х) |
соответствует малое изменение |
|
функционала J[y(x)]. |
|
|
|
В последнем определении |
требуется уточнение |
понятия |
|
малого изменения функции - какие функции и в каком смысле можно считать мало изменяющимися - близкими?
|
Введем понятие |
ε-окрестности |
функции: |
если |
модуль |
|||||||||||||||||||||||||||
разности значений функций у(х) и у1(х) |
не превышает некоторой |
|||||||||||||||||||||||||||||||
произвольной, как угодно малой, величины |
ε |
( |
|
y1 (x)− y(x) |
|
|
≤ε ) |
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
для любого значения аргумента x |
в рассматриваемом интервале |
|||||||||||||||||||||||||||||||
х [а, b], то говорят, что функция у1(х) |
находится в |
ε -окрест- |
||||||||||||||||||||||||||||||
ности функции у(х). |
|
|
|
|
|
|
|
|
|
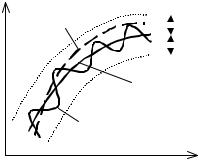
На |
|
рис. |
1.3 |
|
|
|
|
в |
ε- |
|||||||||||||
|
у |
у1(х) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
ε |
|
окрестности функции у(х) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
находятся функции |
|
|
у1(х) и |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у2(х). |
|
Однако, |
|
|
|
|
|
|
если |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
у(х) |
|
функционал J[y(х)] |
|
|
будет |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
зависить от длины кривой, |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
определяемой |
функцией |
||||||||||||||
|
|
|
|
|
у2(х) |
|
|
|
|
|
|
|
|
|
аргумента |
функционала |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
(например, масса кривой с |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
заданной |
|
|
|
вдоль |
|
|
|
|
|
нее |
||||||
Рис. 1.3. ε - |
окрестность кривой у(х) |
|
плотностью ρ(s)), тогда, |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вероятно, |
|
|
значения |
||||||||||||
у(х) и у1(х) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функционала для функций |
|||||||||||||||||
могут иметь близкие значения, в то время как для |
||||||||||||||||||||||||||||||||
функций у(х) |
и у2(х) |
эти значения могут оказаться существенно |
||||||||||||||||||||||||||||||
различными. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у1(х) - у(х)| < ε, |
||||||||||
|
Если ε-окрестность определяется формулой |
| |
|
|||||||||||||||||||||||||||||
она |
называется ε-окрестностью нулевого порядка - ε0 , а кривые |
|||||||||||||||||||||||||||||||
у(х) |
и у1(х) - кривыми нулевого порядка близости. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Кроме ε - окрестности нулевого порядка, вводится понятие ε- |
|||||||||||||||||||||||||||||||
окрестности |
|
первого |
порядка |
ε1, |
|
для |
которой |
должны |
||||||||||||||||||||||||
выполнятся условия |
|у1(х) - у(х)| |
< |
ε |
|
|
и |
|
′ |
|
|
′ |
|
|
|
|
|
<ε . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
y1 |
( x ) − y ( x ) |
||||||||||||||||||||||||||||
Очевидно, функция y1(x), показанная на рис.3.1, лежит в |
ε- |
|||||||||||||||||||||||||||||||
окрестности первого порядка - ε1, |
а |
функция |
|
|
у2(х) |
- |
|
в |
ε- |
|||||||||||||||||||||||
окрестности |
нулевого порядка - ε0 |
функции у(х). По аналогии |
||||||||||||||||||||||||||||||
вводится |
εn-окрестность функции |
y(x) |
|
- |
ε-окрестность |
n-го |
||||||||||||||||||||||||||
порядка, если выполняются условия: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
y1 (x)− y(x) |
|
<ε , |
|
y1′(x)− y′(x) |
|
<ε , …., |
|
y1′(n)(x)− y( n ) (x) |
|
<ε . |
|||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
Соответствующие кривые являются кривыми |
n-го |
порядка |
|||||||||||||||||||||||||||||
близости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функции, лежащие в εn-окрестности, должны быть п раз дифференцируемы, то есть принадлежать классу Сn.
Вариацией (приращением) аргумента функционала у(х)
называется разность функций у(х) и y1(x) во всем интервале изменения аргумента х [а,b], если функция y1(x) лежит в ε-окрестности функции у(х). Вариация обозначается символом δ :
δ y(x)= y1 (x)− y(x), х [a,b], y(x), y1(x) С. |
(1.1.2) |
Разность значений функционала для двух функций у(х) и
y1(x), лежащих в ε-окрестности, называется приращением |
|||||||
функционала |
|
|
|
|
|
||
|
|
∆J[y(x)]= J [y(x)]− J[y1 (x)]. |
|
||||
Функционал J[y(x)] |
называется непрерывным при у = у0(х) в |
||||||
смысле близости п-го |
порядка, если для любого, как угодно |
||||||
малого, положительного |
δ можно подобрать ε > 0, |
такое что |
|||||
модуль приращения функционала меньше δ, |
если у0(х) |
лежит в |
|||||
εn-окрестности функции |
у(х): |
|
|
||||
∆J[y(x)]= |
|
J[y(x)]− J[y0 (x)] |
|
<δ , |
y( x ), y0 (x) εn . |
||
|
|
||||||
Вариацией функционала J[y(x)] называется линейная часть приращения функционала. Вариация функционала обозначается
δJ[y(x)]:
δ J[y(x)]= L[y(x),δ y(x)].
Представим приращение
|
|
|
|
|
|
функционала в виде суммы |
||||||||||
|
|
|
|
|
|
линейной и нелинейной части |
||||||||||
|
|
|
|
|
|
функционала: |
|
|||||||||
|
∆J[y(x)]= L[y(x),δ y(x)]+ β[y(x),δ y(x)] max |
|
δ y(x) |
|
, |
|
|
(1.1.3) |
||||||||
|
|
|||||||||||||||
где L[y(x),δ y(x)] - линейная |
часть приращения |
функционала |
||||||||||||||
J[y(x)]; |
max|δ y(x)| |
- максимальное значение |
|
приращения |
||||||||||||
аргумента |
у(х) для х |
[а,b]; |
β[y(x),δ y(x)] max |
|
δ y(x) |
|
→ 0 при |
|||||||||
|
|
|||||||||||||||
|
δ y(x) |
|
→ 0 . Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
δJ[y(x)]= lim ∆J[y(x)]= L[y(x),δ y(x)]. |
|
|
|
|
|
(1.1.4) |
||||||
|
|
|
|
|
δ y→0 |
|
|
|
|
|
|
|
|
|
|
|
При исследовании функционалов вариация функционала играет такую же роль, какую дифференциал функции играет в исследовании функций. Свойства оператора вариации δ при его действии на сумму и произведения функций аналогичны свойствам дифференциала функции:
δ[c1 u(x)+ c2 v(x)]= c1 δu(x)+ c2 δv(x);
δ(u v)= u δv + v δu . |
(1.1.5) |
При одновременном действии оператора вариации δ и оператора дифференцирования d или оператора интегрирования (для собственных интегралов) они взаимно перестановочны:
δ |
du |
= |
d |
δu , |
δ ∫b u(x)dx =∫b δu(x)dx . |
(1.1.6) |
||
dx |
dx |
|||||||
|
|
|
a |
a |
|
|||
Эти свойства сохраняются и для частных производных и при интегрировании по области двухмерного и трехмерного пространств.
Вариацию функционала можно также определить, как |
||||
производную от функционала J[y(x)+α δ y(x)] |
, как |
функции |
||
двух переменных х, α по параметру α при α = 0: |
|
|||
δJ[y(x)]= ∂J[y(x)+α δ y(x)] |
|
. |
|
(1.1.7) |
|
|
|||
∂α |
|
α=0 |
|
|
|
|
|
|
|
1.2.Условия экстремума функционала. Основная лемма вариационного исчисления. Формула Эйлера.
Определение. Функционал J[y(x)] достигает на кривой
y = у0(х) максимума, если значения функционала на любой кривой у(х), близкой к у0(х), не больше, чем J[y0(x)], т.е.
∆J[y(x)]= J[y(x)]− J[y0 (x)]= J[y(x)− y0 (x)]≤ 0 . |
(1.2.1) |
||
Если ∆J ≤ 0 , причем ∆J = 0 только при у(х) = y0(х), то |
|||
говорят, что на кривой y0(х) достигается строгий максимум. |
|
||
Аналогично определяется кривая у = y0(х), |
на |
которой |
|
достигается минимум функционала. В этом случае |
∆J ≥ 0 |
для |
|
всех кривых, близких к кривой у = y0(х).
Теорема. Если функционал J[y(x)] достигает максимума или минимума при у(х) = y0(х), где у(х) - внутренняя точка области определения функционала, то при у(х) = y0(х) вариация функционала равна нулю
δ J[y0(x)] = 0. |
(1.2.2) |
Доказательство.
При фиксированных y0(х) и δу J[y0(x) + α δy(x)] = ϕ(x,α) является функцией параметра α, которая при α = 0, по предположению, достигает максимума или минимума, и, следовательно, в соответствии с формулой (1.1.7) имеем
|
∂ |
J[y0 (x)+α δ y(x)] |
|
∂ϕ(α,x) |
|
= 0 , |
||
|
|
= |
|
|||||
|
|
∂α |
|
|||||
|
∂α |
|
α=0 |
|
|
α=0 |
||
т.е. δJ[y0(x)] = 0. |
|
|
|
|
||||
|
J[y0(x)] |
|
(1.2.3) |
|||||
Определение функционала |
|
включает понятие |
||||||
близости функций. Однако, как отмечалось выше, различают функции, близкие по модулю разности функций - ε-окрестность нулевого порядка, или функции, близкие как по разности функций, так и по направлению касательных - ε-окрестность первого, а при необходимости используется и ε-окрестность более высокого порядка. Поэтому различаются и типы экстремумов функционалов.
Если функционал J[y(x)] достигает максимума или минимума по отношению ко всем кривым, для которых модуль разности
|у(х) - y0(x)| мал, т.е. в |
ε-окрестности нулевого порядка, то |
||
экстремум (максимум, минимум) называют сильным. |
|
||
Если функционал J[y(x)] достигает экстремума лишь по |
|||
отношению к кривым, лежащим в |
ε-окрестности первого |
или |
|
более высокого порядка |
функции |
y0(x)), то максимум |
или |
минимум называется слабым.
Очевидно, если на кривой у(х) = y0(x) достигается сильный экстремум функционала, то тем более достигается и слабый, так как кривая, близкая в ε-окрестности п-го порядка, близка в ε-окрестности любого более низкого порядка, в том числе в ε-окрестности первого порядка. Однако возможно на кривой достигается слабый максимум или минимум и в то же время не достигается сильный максимум или минимум.
При доказательстве многих положений вариационного исчисления используется следующая лемма, которая называется
основной леммой вариационного исчисления:
