b

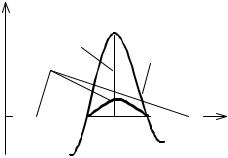
если для любой непрерывной функции η(х) С0 , η(а) = η(b) = 0,

х [a,b]

∫b F(x) η(x)dx = 0 ,

a

где функция F(x) непрерывна на отрезке интегрирования [a,b] (F(x) С0), то F(x) ≡ 0 на том же отрезке.

x1 < x0 < x2 и равно нулю вне этого отрезка. Так как, предположив, что в некоторой точке x0 отрезка [а, b] F(х0) ≠ 0, мы пришли к противоречию с условиями леммы, то, следовательно, F(x) ≡ 0 на отрезке интегрирования [а, b] .

Замечание. Доказательство леммы не изменится, если функции F(x) и η(х) будут принадлежать к классу Сn, то есть быть непрерывными и иметь непрерывные производные до п-го порядка.

Основная лемма может быть доказана также для произвольной области D на плоскости, т.е., если

при произвольной функции η(х,у) С (η(х,у) = 0 на границе области D), то F(x,y) ≡ 0.

Далее лемма может быть обобщена на трехмерное и любое n- мерное пространство.

Как видно из приведенных выше примеров функционалов, большинство из них представляются в виде интегралов от некоторого класса функций в ограниченной области интегрирования.

J[y(x,α)]= ∫b F[x, y(x), y′(x)]dx .

a

По аналогии с дифференциальным исчислением можно показать, что на функции у(х), удовлетворяющей условию (1.2.5), достигается минимум функционала, если вторая вариация функционала больше нуля

δ2J[y(x)] = δ{δ J[y(x)]} > 0,

имаксимум функционала, если вторая вариация меньше нуля

δ2J[y(x)] = δ{δ J[y(x)]} < 0.

Если вторая вариация функционала равна нулю

функции y0(x) - признак стационарности функционала.

Достижение функционалом стационарного значения соответствует точке перегиба функции в дифференциальном исчислении.

Во многих вариационных задачах существование решения очевидно из физического или геометрического смысла задачи. Тогда, если решение уравнения Эйлера, удовлетворяющее граничным условияv единственно, то эта экстремаль и будет единственным решением рассматриваемой задачи.

Без доказательства приведем некоторые обобщения формулы

и их вариации также являются независимыми, и, следовательно, для достижения минимума функционала должны равняться нулю вариации по каждому из независимых аргументов (функций)

Частные производные по х, у, z являются полными частными производными и вычисляются по формулам:

Аналогично могут быть получены формулы для полных частых производных подынтегральной функции F при вариациях функционала по аргументам ϕ(x, у, z), ψ(x, у, z).

Приведенные сведения из вариационного исчисления отражают лишь минимум необходимых сведений, используемых для доказательства вариационных принципов теории упругости. Для более полного знакомства с вариационными методами можно обратиться к литературе по вариационному исчислению приведенной в конце пособия.

1.3. Задачи на экстремум функционалов.

Рассмотрим несколько задач на минимум (экстремум) функционалов и использование формулы Эйлера.

Пример 1. Определить функцию у(х), на которой достигается экстремум функционала

Тогда получаем

Fy = ∂∂y (y 2 − y′2 )= 2y ; Fy′ = ∂∂y′ (y 2 − y′2 )= −2y′;

уравнению второго порядка с постоянными коэффициентами

решение дифференциального уравнения (1.2.2) в виде:

у(х) = С1 sin x + C2 cos x.

y( x ) = 2sh1 2 (ex − e−x )= shshx2 .

Пример 3. Определить функцию, на которой достигается экстремум функционала

Окончательно получаем, что экстремум рассматриваемого функционала реализуется на кривой

y(x)= πx − 12 sin x .

Пример 4. Найти линию минимальной длины, соединяющей две точки на плоскости с координатами х1, у1 и х2, у2.

Хотя ответ на этот вопрос ясен, получим его, используя формулу Эйлера.

Расстояние между двумя точками плоскости определяется функционалом:

Так как функция F не зависит от у(х) , то Fy = 0, и формула Эйлера запишется в виде:

dFdxy′ = Fy′y′ y′′ = 0 ,

откуда получим, что экстремуму функционала соответствуют условия:

Решением первого дифференциального уравнения будет функция у(х) = С1х + С2, которая определяет прямую линию на плоскости. Из граничных условий получим:

y(x1) = C1x1 + С2 = y1 и y(x2) = C2x2 + С2 = y2.

Решая полученную систему уравнений, имеем

и окончательно получим уравнение прямой, проходящей через заданные точки, известное из курса аналитической геометрии:

y( x ) = y1 + y2 − y1 (x − x1 ) x2 − x1

Можно показать, что второе условие экстремума рассматриваемого функционала не даст новых, отличных от полученного, решений.

Таким образом, как и следовало ожидать, мы получили, что кратчайшим расстоянием между двумя точками на плоскости является прямая линия.

Рассмотрение задачи о геодезической линии (линии кратчайшего расстояния) на криволинейной поверхности, требует дополнительных знаний дифференциальной геометрии и в данном пособии не рассматривается.

Пример 5. Рассмотрим задачу о минимальной поверхности вращения.

Найти кривую у(х), проходящую через точки у(х0)= у0, у(х1)= у1, которая при вращении вокруг оси х образует поверхность минимальной площади.

Площадь поверхности вращения определяется интегралом

не зависит напрямую от х (F = F[y(x),y'(x)]), то в формуле (1.2.6) частная производная по х равна нулю, и, следовательно, условие Эйлера принимает вид:

Если выражение (1.3.7) домножить на у', то оно становится полной производной по х

(Fy − Fyy′ − Fy′y′ y′′) y′ = dxd (F − Fy′ y′)= 0

. 1.3.8)

В справедливости полученного выражения можно убедится непосредственным дифференцированием:

Интегрирование последнего выражения дает

или

Формула (1.3.10) определяет семейство кривых, называемых цепными линиями, от вращения которых вокруг оси х получаются поверхности минимальной площади, называемые катеноидами.

Пример 6. Получить кривую, минимизирующую функционал:

где у(х) - прогиб балки; ЕIz - изгибная жесткость балки (Iz - момент инерции поперечного сечения балки, может быть переменным); q(x) - интенсивность распределенной нагрузки.

Функционал (1.3.11) представляет собой полную энергию деформации изгиба балки, а минимизация этого функционала при заданных граничных условиях, как следует из принципа Лагранжа, который будет рассмотрен ниже, дает форму прогиба балки от действия распределенной нагрузки q(x). Приведенные граничные условия соответствуют шарнирному опиранию балки.

и условие Эйлера определяется формулой (1.2.7):

и, следовательно, условие минимума функционала получим в виде:

Таким образом, условию Эйлера минимума функционала (1.3.12) соответствует дифференциальное уравнение изгиба балки.