
attachment
.pdf
|
|
|
|
|
d r . |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Радіус-вектор r розкладемо по ортах системи координат: |
|
|
|
|
|
|||||||||||
|
|
|
|
r ix jy kz . |
|
|
|
|
|
|
|
(а) |
||||
|
|
|
z |
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M(x,y,z) |
|
|
|
|
|
k |
|
|
|
|
|
|||
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
k |
|
N |
|
|
|
|
|
|
|
|
N2 |
|
vN |
||
|
|
|
y |
|
|
|
|
|
|
|
|
|
2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
i |
O |
2 |
|
|
|
|
|
O |
|
|
|
|
y |
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
x |
|
|
j |
|
|
|
|
|
N |
|
|
|
|
|
|
|
N1 |
|
|
|
|
|
|
|
i |
|
|
j |
|
|
|
||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vN |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
рис. 1.15 |
|
|
|
|
|
|
рис. 1.16 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Координати точки x, y, z і орт |
k |
не залежать від часу: орти i |
і |
j |
є функції |
|||||||||||
часу.Отже, |
|
|
d r x di |
|
|
|
|
|
|
|
|
|
||||
|
|
|
y d j . |
|
|
|
|
|
|
(в) |
||||||
|
|
|
|
dt |
|
dt |
dt |
|
|
|
|
|
|
|
||
визначимо похідні |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
di |
|
і dj |
|
|
|
|
|
|
|
|
|
|
di |
|
|
|
dt |
|
dt |
|
|
|
|
|
|
|
|
|
Вектор |
|
dt можна |
розглядати |
як |
швидкість точки |
N1 , |
що |
викреслює |
||||||||
годограф вектора i . Модуль цієї швидкості |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
N |
1 |
|
|
|
|
|
|
|
(с) |
|||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Вектор |
N |
|
напрямлений |
по |
дотичній |
до |
кола |
радіуса |
i |
, |
тобто |
|||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
перпендикулярно до осі Ox і паралельно осі Oy (рис.1.16). |
|
|
|
|
|
|
||||||||||
Згідно з цим дістанемо |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
di |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N1 |
j . |
|
|
|
|
|
|
|
(d) |
|||
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
Якщо кутова швидкість додатня, то швидкість |
|
|
|
|
|
|||||||||||
N |
збігається з ортом |
j . |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
Аналогічно знайдемо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
d j |
N 2 |
i . |
(е) |
|
dt |
||||
|
|
|
21

Згідно з (b), (d) і (е) швидкість точки М |
|
|
j x i y . |
(f) |
|
З курсу векторної алгебри відомі співвідношення |
|
|
i j k; |
j k i; 0 k k . |
(g) |
Підставивши (g) в (f), дістанемо |
|
|
k i x k jy k kz . |
(h) |
|
|
|
|
Винесемо за дужки k |
|
|
k (ix jy kz). |
(k) |
|
|
|
|
Вектор k називають вектором кутової швидкості : |
|
|
|
k . |
(1.45) |
|
|
|
Як видно з (1.45), вектор напрямлений уздовж осі обертання у той бік, для |
||
якого обертальний рух має напрям |
ходу годинникової стрілки. |
Точка прикладання |
|
|
|
вектора на осі обертання довільна. Отже, ковзний вектор. |
|
|
Тоді (k) набуває вигляду |
|
|
|
r . |
(1.46) |
Цю формулу називають формулою Ейлера.
Вибравши осі координат, як показано на рис.1.16, знайдемо формули для проекцій лінійної швидкості на ці осі:
x y z z y ,
y z x x z ,
z x y y x .
Поняття вектора кутової швидкості і формулу Ейлера дістали, розглядаючи найпростіший обертальний рух тіла – обертання навколо нерухомої осі. Здобуті
висновки буде поширено на більш загальні випадки руху твердого тіла.
Розглянемо вектор кутового прискорення . Кутове прискорення – це вектор, що характеризує бистроту зміни вектора кутової швидкості в часі. Тому
|
|
|
|
d |
. |
|
|
(1.47) |
|
|
|
|
|
|
|||
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
Очевидно, |
вектор |
|
напрямлений по дотичній до годографа вектора кутової |
|||||
швидкості. У розглянутому випадку годографом вектора |
|
є пряма, |
що збігається із |
|||||
віссю обертання. |
Отже, |
при |
обертанні тіла навколо нерухомої осі |
вектор кутового |
||||
|
|
|
|
|
|
|
|
|
прискорення напрямлений вздовж осі обертання. |
|
|
|
|||||
22

1.2.5. Рух вільного твердого тіла. Розподіл лінійних швидкостей і прискорень у вільному твердому тілі
Основна ознака абсолютно твердого тіла – незмінність відстаней між довільними точками такого тіла. Звідси випливає властивість збереження кута між двома довільними прямими, проведеними в абсолютно твердому тілі. Як буде показано далі, цих властивостей досить для визначення основного закону розподілу швидкостей і прискорень у вільному твердому тілі.
Розглянемо |
точку |
M (x, y, z) |
вільного твердого |
|||||||||||
(рис.1.17).З тілом А незмінно зв’язана система координат |
|
|||||||||||||
Oxyz . Точка O1 |
нерухома. Точку O назвемо полюсом. |
|
||||||||||||
|
|
|
|
|
|
|
|
точки M : |
|
|
||||
З рис.1.17 видно, що радіус-вектор r |
|
|
||||||||||||
r rO rOM rO xi y j zk. |
(1.48) |
|
|
|
||||||||||
На підставі (1.48) |
знайдемо швидкість точки М: |
|
||||||||||||
M |
d r |
|
d r0 |
x |
di |
y |
d j |
|
z |
d k |
|
(1.49) |
|
|
|
|
|
dt |
dt |
x |
|||||||||
|
dt |
dt |
|
dt |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Необхідно |
знайти |
похідні |
di |
dt , dj |
dt і |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
dk dt . Для цього скористаємося згаданими
властивостями абсолютно твердого тіла. Розглянемо дві системи рівностей
тіла довільної форми
|
z |
|
A |
|
M |
|
rOM |
|
k |
|
y |
O |
r |
|
|
|
|
i |
j |
|
|
|
r |
|
rO |
|
|
|
O1 |
рис.1.17 |
||
|
|
|
|
|
|
|
i i 1; |
j j 1; k k 1; |
|
|
|
(а) |
|||||||||||||||
|
|
|
|
|
|
|
i j 0; i k 0; |
|
j k 0; |
|
|
(в) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ці рівняння |
означають збереження |
довжин ортів i , |
j , k і |
кутів між ними. |
||||||||||||||||||||||
Диференціюючи рівності (а) за часом, дістанемо |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
di |
|
|
j |
d j |
0; k |
d k |
0. |
|
|
|||||||||||
|
|
|
|
|
|
i |
|
0; |
|
|
|
|
|
|
|
|
(с) |
||||||||||
|
|
|
|
|
|
|
|
dt |
dt |
|
|||||||||||||||||
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Рівності |
(с) |
– умови ортогональності |
векторів |
відповідно |
di dt , |
dj dt і |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
dk |
dt та i , |
j , k . Тому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
di |
|
|
d j |
|
|
|
|
|
|
d k |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
i i ; |
|
|
|
|
j |
j; |
|
|
|
k |
k. |
|
(d) |
||||||||
|
|
|
|
|
|
dt |
dt |
|
|||||||||||||||||||
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Тут i , |
j , k - довільні вектори . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
З рівностей (в), після диференціювання їх за часом, дістанемо |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
d j |
|
|
|
di |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
j |
|
|
0. |
|
|
|
|
|
|
|
(е) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|||
Підставляючи (d) в (е) , маємо
23

i j j j i i 0, |
(g) |
звідки на підставі властивостей змішаного добутку векторів |
|
i i j j i j 0, |
(h) |
або |
|
|
|
|
|
|
( i j ) (i j) 0. |
|
|
|
(і) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Вектор i |
j k 0 . У |
загальному |
випадку |
руху |
вільного |
твердого тіла |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вектор i |
j |
не буде перпендикулярним до орту k . Отже, |
рівність (і) виконується, |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
якщо i j =0, тобто i j . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Аналогічно i k , |
j k . |
|
|
|
|
|
|
|
|
|
|
||||||||
|
Отже |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i j |
k |
. |
|
|
|
(j) |
|||||||
|
а рівності (d) мають вигляд: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
d i |
i; |
d j |
j; |
d k |
|
k. |
(k) |
|||||||||
|
|
|
|
dt |
dt |
dt |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Рівність (1.49), що визначає швидкість точки М на підставі (k) набуває вигляду |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
M O x i |
y j z k , |
|
||||||||||||||
|
або |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
M |
O |
r OM . |
|
|
|
|
(1.50) |
|||||||
|
Рівність (1.50) визначає закон розподілу швидкостей у вільному твердому тілі. |
|||||||||||||||||||
Диференціюючи (1.50) за часом дістанемо закон розподілу прискорень: |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
W M |
W O r OM |
OM . |
|
(1.51) |
|||||||||||
|
|
|
|
|
d , |
OM r OM . |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
У виразах (1.50) |
і (1.51) фізичний зміст векторів |
|
і |
не визначено. Його |
|||||||||||||||
можна визначити, розглядаючи окремі випадки руху тіла. |
|
|
|
|
||||||||||||||||
|
Наприклад, якщо вісь обертання нерухома і полюс знаходиться на цій осі, то |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 =0 |
і r , де - вектор кутової швидкості, напрямлений вздовж осі. |
|||||||||||||||||||
На підставі (1.50) і (1.51) можна зробити висновок:
Рух вільного твердого тіла можна розкласти на два рухи: поступальний, що визначається рухом довільної фіксованої точки тіла, яку називають полюсом, і
обертальний рух навколо осі, що проходить через полюс. Цю вісь називають миттєвою
віссю обертання, а - миттєвою кутовою швидкістю.
З рівності (1.48), як наслідок, випливає важлива теорема.
Теорема. Проекції швидкостей двох точок тіла на пряму, що поєднує ці точки, рівні між собою.
24
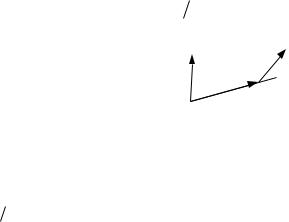
|
Розглянемо точки O і |
M (рис.1.18). Пряма, |
|
що їх поєднує це радіус-вектор |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
r . |
|
|
r |
. Орт e |
вектора r |
дорівнює |
відношенню |
|
|
r |
Помножимо обидві |
||||||
OM |
|
OM |
|
|
|
|
|
|
|
|
OM |
OM |
|
|
сторони (1.50) |
скалярно на |
e , |
тобто знайдемо |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
vM |
|
проекцію цієї рівності на r |
. Другий доданок у |
|
|
|
v |
|||||||||
|
|
|
OM |
|
|
|
|
|
|
|
|
|
O |
|
правій частині (1.50) перпендикулярний до орта |
|
|
|
|
r |
|||||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
. Тому |
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
rOM |
||
|
(V M ) |
(V O ) |
. |
|
|
|
(1.52) |
|
|
O |
||||
|
|
|
|
|
|
|
|
|||||||
|
|
OM |
|
OM |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.18 |
||
|
Приклади |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Розглянемо рівнозмінний обертальний рух тіла навколо нерухомої осі. У цьому |
|||||||||||||
разі кутове прискорення тіла – величина стала ( const) . |
|
|
||||||||||||
|
Згідно з (1.39) |
d dt , або d dt , звідки |
|
|
||||||||||
|
|
|
|
|
|
t C1 . |
|
|
|
|
(а) |
|||
|
Користуючись (1.38), маємо |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
d |
t C1 . |
|
|
|
|
(в) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
dt |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
інтегруючи (в), дістаємо |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
t 2 |
|
|
|
|
|
||||
|
|
|
|
|
|
C t C |
2 |
, |
|
|
(с) |
|||
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
де C1 і C2 - сталі інтегрування, що знаходяться з початкових умов.
Якщо |
|
|
|
|
|
|
|
|
|
||
|
|
t 0 0 , |
|
|
t 0 0 |
(d) |
|||||
|
|
||||||||||
то з (в) і (с) дістанемо |
|
|
|
|
|
|
|
|
|
||
0 C1 , 0 C2 . |
|
(е) |
|||||||||
Підставляючи (е) в (а) і (в), дістаємо закон рівнозмінного обертального руху тіла |
|||||||||||
навколо нерухомої осі: |
|
|
|
|
|
|
|
|
|
||
|
|
|
t |
t 2 |
. |
(1.53) |
|||||
0 |
|
||||||||||
|
|
|
|
0 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
і закон зміни кутової швидкості в цьому русі: |
|
|
|||||||||
|
|
0 |
t . |
|
(1.54) |
||||||
25

1. Два шківи I і II з’єднано |
|
|
|
|
|
|
|
|
K |
|
|
|
||||||||||
нескінченним |
пасом |
|
(рис.1.19). |
|
|
|
|
|
|
|
|
II |
||||||||||
|
|
|
|
|
N |
|
|
|
|
|||||||||||||
Радіуси |
шківів |
|
відповідно |
|
|
|
|
|
R2 r2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
R 0,25 |
і |
R 0,5 |
м. |
|
|
|
I R1 |
|
|
|
|
|||||||||||
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
R1 |
M |
|
|
|
|||
Внутрішній |
радіус |
|
шківа |
II |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
r 0,2 м. |
Знайти |
швидкість |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
точок паса і кутові швидкості |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
обох шківів, якщо рівняння руху |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
тягаря |
III |
x 4t 2 |
|
( x - |
|
в |
|
|
|
|
|
|
III |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
метрах, |
t - в секундах). |
|
|
|
|
|
|
|
|
|
|
|
|
|
рис. 1.19 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Припускаючи, що рух каната відбувається без ковзання, дістаємо, що швидкість |
||||||||||||||||||||||
точки стикання M каната зі шківом II дорівнює швидкості тягаря III. |
|
|
|
|||||||||||||||||||
З рівняння руху тягаря ця швидкість x 8t м с . |
|
|
|
|
|
|
|
|||||||||||||||
Отже, кутова швидкість шківа II |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
8t |
40t c 1 . |
|
|
|
||||||||
|
|
|
|
|
|
|
|
M |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
r2 |
|
0, 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Оскільки пас рухається без ковзання, то точки ободів шківів мають однакову |
||||||||||||||||||||||
швидкість M K , і |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
I R1 II R2. |
|
|
|
|
|
|
|
|||||||||
Звідси |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
II R2 |
|
40t 0,5 |
80t |
c 1 . |
|
|
|
|||||||||
|
|
|
|
I |
|
|
|
|
||||||||||||||
|
|
|
|
|
R1 |
|
|
0,25 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3. Тіло обертається навколо нерухомої осі згідно з законом t 2 . Визначити
швидкість точки тіла на відстані r 0,5 м від осі обертання в момент, коли25 рад.
Відповідь: 5 м с .
с .
4.Закон обертального руху тіла 1 4t . Визначити прискорення точки тіла на відстані r 0,2 м від осі обертання.
5.Кутова швидкість колеса I змінюється за законом 1 t 2 . Визначити
прискорення тягаря 3 в момент часу t 2 с. Якщо радіуси R1 1м, R2 0,8 м і r2 0,4 м (рис.1.20).
Відповідь: 2 t м с2 .
с2 .
1.2.6.Плоскопаралельний рух твердого тіла. Рівняння руху
26

Плоскопаралельним називають такий рух твердого тіла, під час якого всі точки тіла рухаються паралельно певній нерухомій площині, яку називають основною.
Багато механізмів, які зустрічаються в практиці, належать до так званих плоских механізмів. Тому вивчення плоскопаралельного руху тіла має істотне практичне значення.
Плоскопаралельний рух можна розглядати як окремий випадок руху вільного твердого тіла.
Покажемо, що з означення плоскопаралельного руху випливає можливість звести задачу вивчення руху тіла в просторі до задачі вивчення руху плоскої фігури в площині.
Теорема. Будь-яке переміщення плоскої фігури в її площині може бути здійснено поступальним переміщенням разом з вибраним полюсом і обертальним рухом навколо вибраного полюса.
Тіло перебуває в плоскопаралельному русі (рис.1.21), площина xOy - основна.
z |
B |
|
|
η |
|
|
|
S |
y |
ξ |
|
||
|
A |
|
|
|||
|
|
|
|
|||
|
|
|
|
|
φ |
|
O |
|
y |
|
|
O(x0, y0) |
x |
|
|
O1 |
|
|
||
x |
|
|
|
|
|
рис. 1.21 рис. 1.22
Зробимо перетин тіла площиною, паралельною основній. Розглянемо рух прямої
AB - поступальний. Отже, рух довільної точки A цієї прямої визначає цей поступальний рух. Якщо повторити ці міркування для будь-якої точки плоскої фігури
S , то можна твердити, що рух тіла повністю визначається рухом цієї фігури S . Складемо рівняння руху плоскої фігури. Виберемо дві системи координат:
нерухому Oxy і незмінно зв’язану з плоскою фігурою O . Положення системи координат O повністю визначає положення плоскої фігури (рис.1.22). Якщо кожному моментові часу t поставити у відповідність значення величин x0 , y0 , , то дістанемо рівняння, які є законом руху плоскої фігури:
x0 |
x0 (t) ; |
(1.55) |
y0 |
y0 (t) ; |
(1.56) |
(t) . |
(1.57) |
|
Ці рівності – кінематичні рівняння плоскопаралельного руху твердого тіла.
Структура рівнянь показує, що рух плоскої фігури можна розглядати як складний: поступальний разом з полюсом O (рівняння (1.55), (1.56)) і обертальний
навколо полюса O (рівняння (1.57)). Якщо перенести полюс із точки O в іншу точку, рівняння (1.57) не зміниться, зміняться лише рівняння (1.55) і (1.56). З цих міркувань можна зробити висновок: при плоскопаралельному русі твердого тіла характеристики
обертального руху ( кут повороту , кутова швидкість , кутове прискорення
) не залежать від вибору полюса.
27

Розглядаючи плоскопаралельний рух як окремий випадок руху вільного твердого тіла, можна зобразити і у вигляді векторів, перпендикулярних до площини руху тіла.
Рівняння руху довільної точки |
M тіла знайдемо, скориставшись формулами |
||||
перетворення координат: |
|
|
|
|
|
x x0 |
cos sin ; y y0 |
sin cos .(1.58) |
|||
1.2.7. Розподіл лінійних швидкостей у тілі при |
плоскопаралельному |
||||
|
|
|
русі |
|
|
Розглянемо плоскопаралельний рух тіла як окремий випадок руху вільного |
|||||
твердого тіла, скориставшись співвідношенням (1.50): |
|
||||
|
|
|
|
|
|
|
M O r OM . |
(а) |
|||
Позначимо другий доданок у правій частині виразу (а): |
|||||
|
|
|
|
|
|
|
OM |
r OM . |
(1.59) |
||
|
|
|
|
M плоскої фігури навколо |
|
де |
- швидкість обертального руху точки |
||||
OM |
|
|
|
|
|
полюса. Тоді (а) має вигляд (рис.1.23) |
|
|
|
|
|
|
|
|
|
||
|
M |
O |
OM . |
(1.60) |
|
Цей вираз є законом розподілу швидкостей у тілі при плоскопаралельному русі.
|
|
|
|
|
vOM |
||
|
vM |
|
|
O |
|
r |
|
r OM |
M |
||
|
|||
|
|||
vO |
|
vO |
|
|
|
|
|
r |
|
||
|
|
r |
рис.1.23
|
|
|
|
Зауважимо, |
що |
вектор |
|
OM
перпендикулярний до вектора r .
OM
Таким чином, швидкість довільної точки плоскої фігури дорівнює векторній сумі швидкостей полюса і обертального руху точки навколо полюса.
Наслідок. Проекції векторів швидкості кінців незмінного відрізка плоскої фігури на напрямок цього відрізка рівні між собою.
прОМ 0 прОМ М
1.2.8. Миттєвий центр швидкостей та способи його знаходження.
|
Із (1.60) |
можна зробити висновок, що в кожний момент часу існує точка, для якої |
|
|
|
OM |
OM , |
тобто швидкість якої дорівнює нулеві. Цю точку називають миттєвим |
центром швидкостей (МЦШ).
Отже, МЦШ – називається точка плоскої фігури швидкість якої дорівнює нулю в даний момент часу.
Якщо полюс вибрати в миттєвому центрі швидкостей, то на підставі (1.60)
|
. |
M |
OM |
28

|
|
Швидкості точок плоскої фігури можна розглядати як швидкість її обертального |
||||||||||||||
руху навколо миттєвого центра швидкостей. Тому миттєвий центр швидкостей |
||||||||||||||||
називають ще миттєвим центром обертання. |
|
|
|
|
|
|
|
|||||||||
|
|
Найчастіше МЦШ позначають P . |
|
|
|
|
|
|
|
|||||||
|
|
Розглянемо побудову миттєвого центра швидкостей. Для цього існує кілька |
||||||||||||||
способів. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Якщо відома швидкість 0 |
певної точки O фігури і миттєва кутова швидкість |
|||||||||||||
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
OP , |
|
, |
то |
миттєвий центр |
швидкостей (рис.1.24) |
знайдемо |
на |
прямій |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
перпендикулярній до 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Дійсно, виберемо |
P за полюс і знайдемо швидкість точки O : |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
O P PO |
PO ; |
|
|
|
|
P |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
vPO |
|
||
|
|
|
|
PO PO і PO OP . |
|
|
|
|
|
|||||||
|
|
|
|
|
|
r |
|
|
||||||||
|
|
|
|
|
|
|
|
|
vO |
|||||||
|
|
|
|
|
|
|
|
O . |
|
|
|
|
|
|
|
|
|
|
|
|
|
PO |
|
|
|
|
|
|
r |
||||
|
|
Звідси |
|
|
(1.61) |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
vO |
|
|
|
|
|
|
|
|
|
|
|
|
PO , |
|
|
|
|
|
|
Миттєвий |
центр швидкостей |
лежить на |
прямій |
|
|
|
|
r |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рис. 1.24 |
|
перпендикулярній |
до вектора |
0 , |
на |
відстані |
OP |
. |
|
|
||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
Відрізок |
PO відкладається від точки O у напрямі, що визначається знаком вектора |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Нехай відомі прямі, |
уздовж |
яких напрямлені |
|
швидкості двох точок А і В |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
плоскої фігури (рис.1.25), |
і відома швидкість точки A . Розглянемо швидкості |
A і |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B як |
швидкості |
обертального руху |
навколо |
|
|
|
P |
|
||||||||
миттєвого центра обертання. Ці швидкості мають |
|
|
v A |
|
|
|||||||||||
бути перпендикулярні до радіусів обертання |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
PA |
|
|
|
|
|
|
|
і PB. Отже, проводимо PA A і |
PB B . |
|
|
vB |
A |
|
|
|
||||||||
|
|
У точці їх перетину знаходиться миттєвий |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
C |
|||||||||
|
|
P швидкостей. Застосувавши формулу |
|
|
|
|
||||||||||
центр |
|
|
|
|
|
|||||||||||
|
|
|
B |
vC |
|
|||||||||||
(1.61), дістанемо: |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
A |
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рис.1.25 |
|
|
|||||
|
|
|
|
|
AP , BP |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Звідси |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
AP |
|
|
|
|
|
(1.62) |
|
|
|
|
|
|
|
|
|
B |
BP |
|
|
|
|
|
|
|
|
|
Відношення швидкостей двох точок плоскої фігури дорівнює відношенню їхніх |
||||||||||||||
відстаней від миттєвого центра швидкостей. Формулу (1.62) можна записати інакше: |
||||||||||||||||
|
|
|
|
|
A |
|
B |
D ... |
. |
|
|
|
(1.63) |
|||
|
|
|
|
|
AP |
BP |
DP |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
29 |
Установленими формулами широко користуються при розв’язуванні задач, у яких треба визначити швидкості точок тіла при плоскопаралельному русі (наприклад, точки
D). Для цього досить з’єднати точку |
D з миттєвим центром і провести перпендикуляр |
|
|
|
|
до DP . Напрям швидкості |
знаходимо згідно з напрямом обертання плоскої фігури |
|
|
D |
|
|
|
|
навколо полюса. Модуль вектора |
обчислюємо з пропорції (1.63). |
|
D
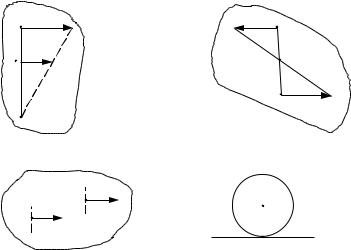
3. Існує ще кілька окремих випадків визначення миттєвого центра швидкостей:
а) швидкості двох точок тіла паралельні, нерівні і мають один напрям (рис.1.26,а); б) швидкості двох точок тіла паралельні, нерівні і мають різні напрями
(рис.1.26,б);
в) швидкості двох точок тіла паралельні, рівні, напрямлені в один бік (рис.1.27).
У цьому разі миттєва кутова швидкість 0 і тіло в цей момент часу виконує миттєвий поступальний рух;
г) у деяких випадках можна знайти положення миттєвого центра швидкостей з умови кочення без ковзання: миттєвий центр знаходиться в точці дотику тіла з нерухомою поверхнею (рис.1.28).
|
|
|
|
|
|
vA |
vA |
|
A |
A |
|
|
|
|
|
|
|
||
B |
vB |
|
|
P |
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
vB |
|
P |
|
|
|
|
|
|
|
|
|
а |
|
б |
|
|
|
рис.1.26 |
|
|
|
|
|
|
|
|
A |
v A |
B |
vB |
|
|
|
|
P |
|
|
|
|
|
|
рис.1.27 |
рис.1.28 |
|
Зауважимо, що під час руху тіла положення миттєвого центра швидкостей змінюється. Геометричне місце миттєвих центрів швидкостей, віднесене до рухомої або нерухомої системи координат, називають відповідно рухомою або нерухомою центроїдою. Центроїдою називається геометричне місце миттєвих центрів швидкостей. З цією геометричною інтерпретацією плоскопаралельного руху пов’язана теорема Пуансо.
Теорема Пуансо. Під час руху плоскої фігури рухома центроїда котиться по нерухомій без ковзання.
Наприклад, при кочені циліндра по горизрнтальній площині (рис. 1.28) нерухома центроїда – горизонтальна пряма, а рухома – коло. В кожний момент часу рухома і нерухома центроїди мають загаліну точку дотику – миттєвий центр швидкостей Р, тобто точку, швидкість якої дорівнює нулю.
30
