
Лекции_1_курс
.pdf
Государственное образовательное учреждение высшего профессионального образования «РОССИЙСКИЙ УНИВЕРСИТЕТ ДРУЖБЫ НАРОДОВ»
Факультет физико-математических и естественных наук
А.А.Балмашнов, С.П.Степина
ОБЩАЯ ФИЗИКА. МЕХАНИКА И МОЛЕКУЛЯРНАЯ ФИЗИКА
КОНСПЕКТ ЛЕКЦИЙ
Для студентов I курса инженерного факультета направлений «Строительство» и «Горное дело»
Москва Издательство Российского университета дружбы народов
2012
1
У т в е р ж д е н о
РИС Ученого совета Российского университета дружбы народов
Балмашнов А.А., Степина С.П.
Экспериментальная физика: Конспект лекций. –– М.:
Изд-во РУДН, 2012. – 162 с.
Для студентов I курса инженерного факультета направлений «Строительство» и «Горное дело».
Конспект лекций подготовлен на кафедре экспериментальной физики.
©Балмашнов А.А., Степина С.П. 2012
©Издательство Российского университета дружбы народов, 2012
2
РАЗДЕЛ I
МЕХАНИКА ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТЕЛ
1. Кинематика
1.1. Основные понятия кинематики
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин его вызывающих.
Механическим движением тела называют изменение его положения в пространстве относительно других тел.
Механическое движение относительно. Движение одного и того же тела относительно разных тел различно. Для описания движения тела нужно указать, по отношению к какому телу рассматривается движение. Это тело называют телом отсчета.
Система координат, связанная с телом отсчета образует
систему отсчета.
С кинематической точки зрения все характеристики движения относительны и все системы отсчета равноправны. Это позволяет при решении той или иной задачи выбрать наиболее рациональную систему отсчета.
Любое реальное тело деформируемо и имеет определенные размеры. Однако, если изменениями в расстояние между двумя произвольно выбранными элементарными объемами тела в процессе изучаемого движения, можно пренебречь, то такое тело можно считать абсолютно твердым. Тело можно считать материальной точкой, если можно пренебречь его размерами по сравнению с пространственными масштабами изучаемого движения.
Положение материальной точки (С) в пространстве характеризуется радиус-вектором rc , которому в Декартовой системе координат соответствуют определенные значения xc , yc, zc .
3

rrc =  xc2 + yc2 + zc2 .
xc2 + yc2 + zc2 .
Уравнения, позволяющие найти положение перемещающегося в пространстве тела в любой момент времени,
называются кинематическими уравнениями движения.
xc = fx (t), yc = f y (t), zc = fz (t)
С точки зрения кинематики, движение материальной точки характеризуется формой траектории, длиной пройденного путиr
( l ), вектором скорости (V ) и вектором ускорения ( a ).
Вспомогательную роль играет вектор перемещения ( S ). Траекторией движения будем называть воображаемую
линию, которую описывает тело (материальная тока) в процессе своего движения.
Длина пути определяется расстоянием, пройденным телом (материальной точкой) вдоль траектории движения.
Вектор перемещения характеризует перемещение тела в пространстве, он соединяет местоположения тела в различные моменты времени. При прямолинейном движении вектор перемещения направлен вдоль траектории и по модулю равен длине пройденного пути. При криволинейном движении вектор перемещения замыкает соответствующую рассматриваемому
промежутку времени часть траектории. Если в момент времени t1 тело находилось в точке А, а в момент времени t2 - в точке В, то перемещению за промежуток времени t = t2 − t1 соответствует
вектор, соединяющие эти точки. y
А В
S
x
z
Рис. 1.1. 4
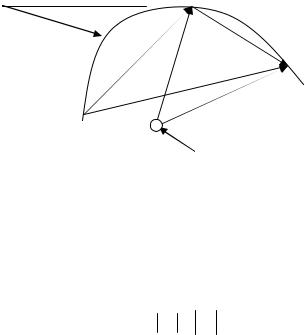
Величина вектора перемещения с одной стороны определяется разностью радиус-векторов, характеризующих положение тела (материальной точки) в различные моменты времени ( r1 − r2 = r ) и разностью векторов перемещения
относительно некоторой точки С ( S1 − S2 = S ), соответствующей положению тела в момент времени предшествующий t1 , с другой стороны, причем rr = S (см. рис. 1.2).
Траектория движения А
|
|
S1 |
|
|
rr = |
S |
|
|
|
r1 |
В |
|
|
||
|
|
|
|
|
|||
|
С |
S2 |
|
|
r2 |
|
|
|
|
|
Тело отсчета |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.2. |
|
|
|
|
Если |
перейдем |
от конечного |
промежутка |
времени t к |
|||
бесконечно |
малому |
dt , то величины, соответствующие |
|||||
изменению радиус-векторов и перемещений будут также
бесконечно малыми, т.е. dr и dS соответственно. При этом, эти вектора будут направлены по касательной к траектории и модули
их величин будут равны dl ( drr = dS = dl ), т.к. радиус кривизны
бесконечно малого участка траектории можно считать равным бесконечно большим, а этот участок прямолинейным.
Вектор скорости
5

В общем случае движения тела неравномерно. Скорость точки меняется. Поэтому вводят понятие средней скорости как величины равной длине пути, пройденной телом за некоторый
промежуток времени Vср |
= |
l′− l |
= |
l . Различия в скоростях в |
|
|
t′−t |
|
t |
моменты времени t и t′ будут тем меньше, чем ближе эти моменты времени. Величина
V = ddtl
называется мгновенной скоростью.
Вспомним, что dl = dS , поэтому можем записать:
Vr = ddtS .
Вектор мгновенной скорости при криволинейном движении, как и элементарное перемещение, направлен по касательной к траектории.
Проекции вектора скорости на оси координат определяют скорости по трем направлениям движения. Ясно, что
Vr =  Vx2 +Vy2 +Vz2 .
Vx2 +Vy2 +Vz2 .
Размерность скорости [V ]= |
см |
(СГС), |
м |
(СИ). |
|
|
|
||||
|
|
|
|
|
|||||||
|
|
с |
|
|
с |
|
|
|
|||
|
Вектор ускорения |
|
|
|
|
|
|
|
|
|
|
|
Ускорение характеризует темп изменения скорости. Как и |
||||||||||
ранее, |
вводится понятие среднего ускорения aср = |
V ′−V |
= |
V |
и в |
||||||
случае |
|
|
|
|
|
|
|
t′−t |
|
t |
|
t → 0 имеем величину, характеризующую мгновенное |
|||||||||||
ускорение: |
|
|
dV . |
|
|
|
|||||
|
|
r |
|
|
|
||||||
|
|
a = |
|
|
|
|
|||||
|
|
dt |
|
|
|
|
|||||
6

Размерность ускорения [a]= смс2 (СГС), см2 (СИ).
Соответствующие компоненты ускорения в Декартовой системе координат могут быть представлены в виде:
ax = |
dVx |
= |
d 2 x |
, |
ay = |
dVy |
= |
d 2 y |
, |
az = |
dVz |
= |
d 2 z |
. |
||
dt |
dt |
2 |
dt |
dt 2 |
dt |
dt 2 |
||||||||||
|
|
|
|
|
|
|
|
|
||||||||
В случае прямолинейного движения вектор ускорения направлен параллельно вектору скорости. Движение может быть ускоренным или замедленным. Ускорение может быть постоянной величиной (равноускоренное или равнозамедленное движение) или переменной.
В случае криволинейного движения всегда существует ускорение, определяющее изменение скорости как векторной
величины, нормальное ускорение ( aN ). Если движение вдоль траектории неравномерно, то есть и тангенциальное ускорения ( aτ ). Нормальное ускорение всегда направлено вдоль радиуса
кривизны траектории движения тела, в направлении изменения скорости как векторной величины, и называется
центростремительным ускорением.
r |
dV |
|
|
r |
|
V |
2 |
|
|
|
|
|
|
|
|||||
aN = |
|
N |
, |
aN |
= |
|
τ |
|
, |
|
|
|
|
||||||
|
|
|
|
||||||
|
dt |
|
|
|
R |
||||
где Vτ - тангенциальная скорость движения тела (скорость вдоль
траектории движения), R - радиус кривизны траектории.
В случае равномерного движения тела (материальной точки) по окружности, aτ = 0 .
Размерность ускорения: [a]= смс2 (СГС), см2 (СИ)
Ниже представлена таблица первых производных и неопределенных интегралов от некоторых элементарных функций, знание которых необходимо для понимания излагаемого далее материала.
7
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = f (t) |
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
∫ydt |
||||||||
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = a |
|
d |
|
(a)= 0 |
|
|
∫adt = at + C |
||||||||||||||||||
a = const |
|
|
|
|
|||||||||||||||||||||
|
dt |
|
|
||||||||||||||||||||||
y = at |
|
d |
|
(at)= a |
|
|
∫atdt = at |
2 |
+ C |
||||||||||||||||
|
|
|
|
dt |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||
y = at 2 |
|
d |
|
(at 2 )= 2at |
∫at 2dt = |
at3 |
|
+ C |
|||||||||||||||||
|
dt |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||
y = atn |
|
d |
|
(at n )= ant n−1 |
∫at ndt = |
atn+1 |
+ C |
||||||||||||||||||
|
dt |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n +1 |
||||||||
y = |
1 |
|
|
d |
|
|
1 |
= − |
1 |
|
∫ |
1 |
dt = |
1 |
ln(t)+ C |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
at |
|
|
a |
|||||||||||||
at |
|
dt |
|
|
at 2 |
|
|
||||||||||||||||||
|
|
|
at |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
y =sin at |
|
d |
|
(sin at)= acosat |
∫sin atdt = − |
|
1 |
cos at + C |
|||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
dt |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
||||||
y = cos at |
|
d |
|
(cosat)= −asin at |
∫cos atdt = |
1 |
sin at + C |
||||||||||||||||||
|
|
|
|
dt |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|||||||
где С = const и называется константой интегрирования. При решении задач она определяется какими-либо граничными условиям.
Производная по t |
от произведения двух функций y = f1 f2 |
||||||||||||||||||||||||
|
|
d |
|
(f |
1 |
f |
2 |
)= |
f |
1 |
|
df2 |
+ |
f |
2 |
|
df1 |
|
|
|
|||||
|
|
dt |
|
|
|
dt |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
||||||||||||
Производная по t |
от отношения двух функций y = |
f1 |
|
||||||||||||||||||||||
f2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
df1 − f |
|
df2 |
||||||||||
|
|
|
|
d |
|
f1 |
|
|
f |
2 |
|
1 |
|
|
|||||||||||
|
|
|
|
|
|
|
dt |
|
dt |
|
|
|
|||||||||||||
|
|
|
|
|
|
= |
|
|
|
|
|
|
|||||||||||||
|
|
|
dt |
|
f2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
f2 |
|
|
|
|
|
|
|
|
||||||
8
Пример: определение зависимостей скорости прямолинейного движения и пройденного материальной точкой пути от времени при равноускоренном (равнозамедленном) движении ( a = const).
По определению, мгновенное значение ускорения определяется выражением:
|
|
|
|
|
r |
|
dV |
, |
|
|
|
|
|
|
|
|
a |
= |
dt |
|
|
|
|
которое представим в |
виде: |
dV = ardt . |
Интегрируем |
это |
|||||||
уравнение |
∫ |
dV = |
∫ |
ardt |
1 |
|
и получаем: |
1 |
, |
где |
|
|
|
+ C |
|
V = art + C |
|||||||
Cr1 = const . Найдем ее значение. Предположим, что в начальный момент времени (t = 0) скорость тела была равной Vr0 . Подстановка этого условия в полученное выражение для скорости движения тела приводит к соотношению C1 =V0 Поэтому имеем:
V = art +V0 .
Для нахождения зависимости пройденного телом пути от времени воспользуемся определением мгновенной скорости:
V = |
d |
(x) и полученной зависимостью ее от времени в условиях |
||
|
dt |
Так как dx =Vdt ,имеем: |
||
неизменности величины ускорения. |
||||
x = ∫Vdt + C2 =∫atdt + ∫V0dt + C2 = |
at 2 |
+V0t + C2 , где C2 = const . |
||
|
||||
2 |
|
|||
Как и ранее, определим постоянную интегрирования через начальные условия. Если в начальный момент времени (t = 0)
координата тела была равной x0 , то получаем: C2 = x0 и зависимость координаты тела от времени принимает вид:
x = at 2 +V0t + x0 .
2
9

1.2. Законы сложения скоростей и ускорений
Ранее отмечалось, что абсолютно неподвижных систем отсчета не существует, есть условно неподвижные, т.к. все тела в природе находятся в движении. При переходе из одной системы отсчета в другую, движущуюся относительно первой, возникает вопрос о сложении скоростей и ускорений.
Рассмотрим перемещение материальной точки в системе отсчета, движущейся относительно другой, считаемой неподвижной. Перемещение тела относительно неподвижной
системы отсчета ( Sабс ) определяется его перемещением относительно подвижной системы отсчета ( Sотн ) и перемещением подвижной системой отсчета относительно неподвижной ( Srпер ).
Вследствие этого получаем:
Sабс = Sотн + Sпер
Если эти перемещения происходят за время dt , то можем записать:
dSабс = dSотн + dSпер
и в результате чего имеем:
dSrабс = dSrотн + dSпер
dt dt dt
Последнее выражение представляет собой закон, сформулированный Галилей, закон сложения скоростей
Vабс =Vотн +Vпер ,
который с высокой точностью подтверждается опытом (если скорости не релятивистские).
10
