2.5 Оценки математического ожидания

48

Если параметр σ известен, то равенство (4) определяет интервал

(x −δ ; x +δ ) , т.е. ( x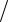 −σ t n ; x +σ t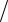 n ) , в котором с вероятностью p = 2Ф(t) заключено подлежащее оценке математическое ожидание величи-

ны X , M ( X ) = a .

В этом случае говорят об интервальной оценке математического ожи-

дания. Интервал (x −δ ; x +δ ) называют доверительным интервалом (δ –

произвольное число), а вероятность p = 2Ф(t) – доверительной вероятностью, соответствующей данному доверительному интервалу ( p иногда называют надежностью γ ).

Разумеется, чем больше взят доверительный интервал, тем больше доверительная вероятность. Увеличивая же число испытаний n можно увеличить доверительную вероятность p = 2Ф(t) , приблизив ее как угодно близко к 1 для любого (даже очень малого) интервала (x −δ ; x +δ ) .

Из соотношений (4), (*) можно вычислить n по заданным σ , δ , p , т.е.

решить задачу о нахождении такого числа испытаний, чтобы данному доверительному интервалу соответствовала данная доверительная вероятность.

Решение.

Вычислим точечную оценку математического ожидания этой величины

p = 2Ф(t) = 2 Ф(1,12) = 2 0,3686 = 0,7372 .

50

σ * 1 − σδ* <σ <σ * 1 + σδ* .

Положив σδ* = q , получим оценку

σ * (1 − q) <σ <σ * (1 + q) .

Значение q определяется из довольно сложного интегрального уравнения. На практике для отыскания значения q по данным значениям n и γ пользуются таблицами.

Заметим, что в задаче об интервальной оценке математического ожидания в случае неизвестной величины σ допустимо взять в качестве σ число

D * , где D * – точечная оценка дисперсии, выражаемая формулой (6).

2.7 Общие замечания об оценке параметров статистического распределения

Рассмотрим кратко общий вопрос об оценке параметров статистического распределения. Оценкой какого-либо параметра распределения по опытным данным является значение некоторой функции ϕ( X1, X 2 , ..., X n ) от

результатов испытаний x1 , x2 , …, xn . Для того, чтобы эта оценка была разумной (приемлемой), функция ϕ должна обладать некоторыми свойствами,

аименно эффективностью, состоятельностью и несмещенностью.

1.Оценка ϕ параметра a называется состоятельной, если

lim P( a −ϕ < ε )=1.

n→∞

2. Оценка ϕ параметра a называется несмещенной, если M (ϕ) = a . 3. Оценка ϕ – эффективна, если D(ϕ) минимальна.

Замечание. Оценка (1) состоятельна и несмещена. Она также эффективна для нормально распределенной случайной величины X .

Оценки (5) и (6) состоятельны, но не являются эффективными.

(5)также не является несмещенной в отличие от (6).

2.8Оценка параметров статистического распределения

сточки зрения генеральной совокупности и выборки

Решение задачи об оценке математического ожидания и дисперсии можно сформулировать, используя понятия генеральной совокупности и выборки.

Пусть дано большое количество N элементов, каждый из которых характеризуется некоторым числом xi , i =1, N . Как известно, такое множество

51

называют генеральной совокупностью ( N – объем генеральной совокупности).

DГ = 1 ∑N (xi − xГ )2 – генеральной дисперсией.

N i =1

Фактическое вычисление xГ и DГ часто оказывается невозможным

вследствие того, что объем генеральной совокупности очень велик. Тогда из генеральной совокупности делают сравнительно небольшую по объему n < N выборку. Выборка производится случайным образом, т.е. для каждого элемента генеральной совокупности вероятность попасть в выборку равна

N1 , так что все элементы имеют равные вероятности и последовательность

испытаний независима.

Таким образом, возникает задача об оценке параметров xГ и DГ по

выборочным данным. Она является частным случаем описанной выше задачи об оценке параметров распределения по результатам испытаний: достаточно рассматривать испытание как выбор одного элемента из генеральной сово-