36
§ 4. Система случайных величин
Пусть в результате некоторого испытания случайные величины X и Y принимают значения x и y . Эта пара чисел задает точку на плоскости. По аналогии с интегральной функцией распределения одной случайной величины можно рассматривать функцию F(t1, t2 ) , равную вероятности
P( X < t1, Y < t2 ) . |
|
Функция |
|
F(t1, t2 ) = P( X < t1, Y < t2 ) |
(1) |
называется интегральной функцией распределения системы двух случайных величин X и Y .
Аналогично, интегральная функция F(t1, t2 , ..., tk ) совместного распре-
деления k случайных величин X1, X 2 |
, ..., X k есть по определению функция |
|
F(t1, t2 , ..., tk ) = P( X1 |
< t1, X 2 < t2 , ..., X k < tk ) . |
(2) |
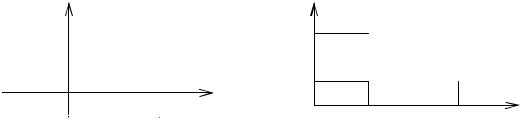
Как видно из рис. 14.8, функция F(t1, t2 ) выражает вероятность попадания точки (x, y) в заштрихованную область.
Y |
|
Y |
|
|
|
||
t2 |
|
d |
|
|
|
|
|
|
|
|
|
|
|||
|
t1 |
X |
c |
|
|
|
|
|
|
|
|
|
|||
|
a |
b |
X |
||||
|
|
|
|||||
Рис. 14.8 |
|
|
|
Рис. 14.9 |
|
||
С помощью интегральной функции распределения F(t1, t2 ) |
можно вы- |
||||||
числить вероятность P(a ≤ X < b, c ≤Y < d ) того, что пара значений величин
X и Y будет удовлетворять неравенствам a ≤ X < b и c ≤Y < d , т.е. принадлежать прямоугольнику (рис. 14.9), а именно
P(a ≤ X < b, c ≤Y < d ) = F(b, d ) − F(b, c) − F(a, d ) + F(a, c) . |
(3) |
|||||||||
Аналогом дифференциальной функции распределения случайной вели- |
||||||||||
чины для пары случайных величин является функция |
|
|||||||||
f (t |
, t |
|
|
д2 F(t |
, t |
2 |
) |
|
|
|
2 |
) = |
|
1 |
|
|
. |
(4) |
|||
|
|
|
|
|
||||||
1 |
|
|
дt1 |
дt2 |
|
|
|
|
||
Можно доказать, что |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
P(t1 ≤ X < t1 + t1, t2 ≤Y < t2 + |
t2 ) ≈ f (t1, t2 ) t1 t2 |
(5) |
||||||||
с точностью до бесконечно малых более высокого порядка малости, чем |
t1 , |
|||||||||
t2 . |
|
|
|
|
|
|
|
|
|
|
37
Функция f (t1, t2 ) называется плотностью вероятности системы ве-
личин X и Y .
Формула (5) оправдывает такое название функции f (t1, t2 ) ( f (t1, t2 )
есть вероятность, отнесенная к единице площади).
Пусть D – область на плоскости переменных x , y и требуется найти вероятность P(( X , Y ) D) , т.е. вероятность того, что значения пары случай-
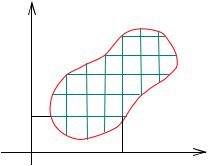
ных величин X и Y определят координаты некоторой точки из D . Разобьем область D на малые прямоугольники со сторонами, парал-
лельными осям координат (рис. 14.10). Тогда искомая вероятность (в соответствии с формулой (5)) будет приближенно равна сумме
∑ f (t1(k ) , t2(k ) ) t1 t2 , k
где t1(k ) , t2(k ) – координаты левой нижней вершины прямоугольника с номе-
ром k . Предел этой суммы (если он существует) по определению равен двойному интегралу
⌠⌠
f (t1, t2 ) dt1dt2 .
⌡⌡
D
Таким образом, получаем формулу
P(( X , Y ) D) = |
⌠⌠ f (t , t |
) dt dt |
2 |
. (6) |
|
|
|
1 2 |
1 |
|
|
|
⌡⌡ |
|
|
|
|
D
Формула (6) есть двумерный аналог формулы
Из формулы (6) следует, что
y
t2(k )
0 |
t(k ) |
x |
|
1 |
|
Рис. 14.10
β
P(α ≤ X < β) = ⌠ f (t) dt .
⌡
α
+∞ |
+∞ |
|
|
|
|
⌠ |
⌠ f (t |
, t |
) dt dt |
=1, |
|
|
|
1 |
2 |
1 2 |
|
⌡ |
⌡ |
|
|
|
|
−∞ |
−∞ |
|
|
|
|
поскольку в этом случае двойной интеграл означает вероятность достоверного события (−∞ < X < +∞, − ∞ <Y < +∞) .
Замечание. По аналогии с одномерной случайной величиной функции
f(t1, t2 ) и F(t1, t2 ) обладают следующими свойствами:
1.0 ≤ F(t1, t2 ) ≤1;
2.F(t1, t2 ) – неубывающая по аргументу функция;
38
3.F(t1, ∞) = F1 (t1 ) , т.к. Y < ∞ – достоверное событие; F(∞, t2 ) = F2 (t2 ) , т.к. X < ∞ – достоверное событие;
4.f (t1, t2 ) ≥ 0 ;
|
+∞ |
+∞ |
|
|
|
|
5. |
⌠ |
⌠ f (t |
, t |
) dt dt |
=1; |
|
|
|
|
1 |
2 |
1 2 |
|
|
⌡ |
⌡ |
|
|
|
|
|
−∞ |
−∞ |
|
|
|
|
xy
6.F(x, y) = ⌠ dt1 ⌠ f (t1, t2 ) dt2 .
⌡ ⌡
−∞ −∞
Рассмотрим теперь совместное распределение двух дискретных случайных величин. Пусть xi и yi – значения случайных величин X и Y , а pi и
qi – соответствующие им вероятности; пусть pij означает вероятность совместного наступления событий X = xi , Y = y j . Соответствие (xi , y j ) → pij
называется совместным распределением пары дискретных случайных величин.
Закон совместного распределения двух случайных величин часто изображают с помощью таблицы:
|
|
|
|
X |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
x1 |
x2 |
|
… |
|
xn |
|
|
y1 |
p11 |
p21 |
|
… |
|
pn1 |
|
Y |
y2 |
p12 |
p22 |
|
… |
|
pn2 |
|
… |
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
ym |
p1m |
p2m |
|
… |
|
pnm |
|
Т.к. события |
( X = xi , Y = y j ) , |
i =1, 2 , ..., n ; j =1, 2 , ..., m |
образуют |
|||||
полную группу, то сумма вероятностей, помещенных во всех клетках таблицы, равна единице.
Зная закон распределения двумерной случайной величины, можно найти законы распределения каждой из составляющих. Действительно, например, события ( X = x1, Y = y1 ) , ( X = x1, Y = y2 ) , …, ( X = x1, Y = ym ) несовместны, поэтому по теореме сложения
P(x1 ) = P( X = x1 ) = p(x1, y1 ) +... + p(x1, ym ) .
Таким образом, для того, чтобы найти вероятность P( X = xi ) , надо просуммировать вероятности столбца xi . Аналогично, для того, чтобы найти вероятность P(Y = yk ) , нужно просуммировать вероятности k -ой строки.