
- •ВВЕДЕНИЕ
- •Глава XIV ТЕОРИЯ ВЕРОЯТНОСТЕЙ
- •Раздел I
- •Виды случайных событий
- •Классическое определение вероятности
- •Основные формулы комбинаторики
- •Статистическое определение вероятности
- •Непосредственное вычисление вероятностей
- •§ 2. Теорема сложения вероятностей несовместных событий
- •§ 3. Условная вероятность. Теорема умножения вероятностей
- •§ 4. Теорема сложения вероятностей совместных событий
- •§ 5. Формула полной вероятности
- •§ 6. Формула Бейеса
- •§ 7. Схема Бернулли
- •Раздел II
- •§ 2. Математическое ожидание, дисперсия и среднеквадратическое отклонение случайной величины, их свойства
- •Свойства математического ожидания
- •Свойства дисперсии
- •Примеры решения задач
- •§ 3. Примеры распределения случайных величин
- •3.1 Биномиальное распределение
- •3.2 Распределение Пуассона
- •3.3 Нормальное распределение
- •3.4. Равномерное распределение
- •3.5 Показательное (экспоненциальное) распределение
- •§ 4. Система случайных величин
- •§ 5. Ковариация и коэффициент корреляции
- •Свойства коэффициента корреляции
- •§ 6. Закон больших чисел. Теорема Чебышева
- •§ 7. Центральная предельная теорема Ляпунова
- •Глава XV МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
- •§ 1. Задачи математической статистики
- •§ 2. Выборочный метод
- •2.1 Генеральная и выборочная совокупности
- •2.2 Статистическое распределение выборки
- •2.3 Эмпирическая функция распределения
- •2.4 Полигон и гистограмма
- •2.5 Оценки математического ожидания
- •2.6 Оценки дисперсии
- •§ 3. О статистической проверке гипотез
- •ПЕРЕЧЕНЬ КОНТРОЛЬНЫХ ВОПРОСОВ
- •КОНТРОЛЬНЫЕ ЗАДАНИЯ
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •ПРИЛОЖЕНИЕ
- •Список рекомендуемой литературы
43
§2. Выборочный метод
2.1Генеральная и выборочная совокупности
Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты.
Определение. Выборочной совокупностью или просто выборкой на-
зывают совокупность случайно отобранных объектов.
Определение. Генеральной совокупностью называют совокупность объектов, из которых производится выборка.
Определение. Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности.
Выборки подразделяют на повторные и бесповторные.
Определение. Повторной называют выборку, при которой отобранный объект перед отбором следующего возвращается в генеральную совокупность.
Определение. Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.
Для того, чтобы по данным выборки можно было достаточно уверенно судить об интересующем признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно ее представляли. Другими словами, выборка должна правильно представлять пропорции генеральной совокупности,
т.е. быть репрезентативной (представительной).
В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если ее осуществить случайно: каждый объект выборки отобран случайно из генеральной совокупности, если все объекты имеют одинаковую вероятность попасть в выборку.
Если объем генеральной совокупности достаточно велик, а выборка составляет лишь незначительную часть этой совокупности, то различие между повторной и бесповторной выборками стирается.
2.2 Статистическое распределение выборки
Пусть для изучения количественного признака X из генеральной совокупности извлечена выборка x1 , x2 , …, xn объема n . Наблюдавшиеся значе-
ния xi признака X называют вариантами, а последовательность вариант,
записанных в возрастающем порядке – вариационным рядом. Число наблюдений значения xi называется его частотой ni , а его отношение к объему
выборки nni = wi – относительной частотой.

44
Определение. Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот.
Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот ( в качестве частоты, соответствующей интервалу, принимают сумму частот вариант, попавших в этот интервал).
Пример 1.
Задано распределение частот выборки объема n = 25
xi |
5 |
25 |
30 |
32 |
Σ |
ni |
7 |
8 |
1 |
9 |
25 |
Написать распределение относительных частот.
Решение.
xi |
5 |
|
25 |
|
30 |
|
32 |
|
Σ |
||||
wi |
|
7 |
|
|
8 |
|
|
1 |
|
|
9 |
|
1 |
25 |
|
25 |
|
25 |
|
25 |
|
||||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.3 Эмпирическая функция распределения
Определение. Пусть известно статистическое распределение количественного признака X .
Эмпирической функцией распределения (функцией распределения вы-
борки) называют функцию F* (x) , определяющую для каждого значения x относительную частоту события ( X < x) , т.е.
F * (x) = nnx ,
где nx – число вариант, меньших x , n – объем выборки.
Свойства эмпирической функции
1.0 ≤ F* (x) ≤1;
2.F* (x) – неубывающая функция;
3.Если x1 – наименьшая варианта, то F* (x) = 0 , при x ≤ x1 ;
если xk |
– наибольшая варианта, то F* (x) =1 при x > xk . |
В отличие от эмпирической функции распределения выборки, функцию |
|
распределения |
F(x) генеральной совокупности называют теоретической |
45
функцией распределения. Различие между эмпирической и теоретической функциями состоит в том, что F(x) определяет вероятность события
( X < x) , а F * (x) относительную частоту этого же события.
Известно, что lim P [ F(x) − F * (x) < ε ]=1 (ε > 0) , т.е. при больших n
n→∞
F(x) и F * (x) мало чем отличаются друг от друга. Уже отсюда следует целесообразность использования эмпирической функции распределения для приближенного представления теоретической (интегральной) функции распределения генеральной совокупности.
Пример 2.
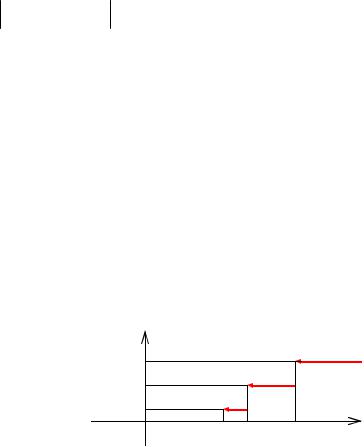
Найти эмпирическую функцию по данному распределению выборки:
|
|
|
xi |
|
4 |
5 |
8 |
Σ |
|
|
|
|
|
|
ni |
|
2 |
5 |
3 |
10 |
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
0, |
x ≤ 4, |
|
F * (x) |
|
|
|
|
||||
|
0,2, |
4 < x ≤ 5, |
1 |
|
|
|
|
||||
|
|
|
|
|
|||||||
F * (x) = |
0,7, |
5 < x ≤ 8, |
0,7 |
|
|
|
|
||||
|
0,2 |
|
|
|
|
||||||
|
1, |
x |
> 8. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||||
|
|
|
|
4 |
5 |
8 |
x |
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
Рис. 15.1 |
|
|
|
2.4 Полигон и гистограмма
Для наглядности строят различные графики статистического распределения, в частности, полигон и гистограмму.
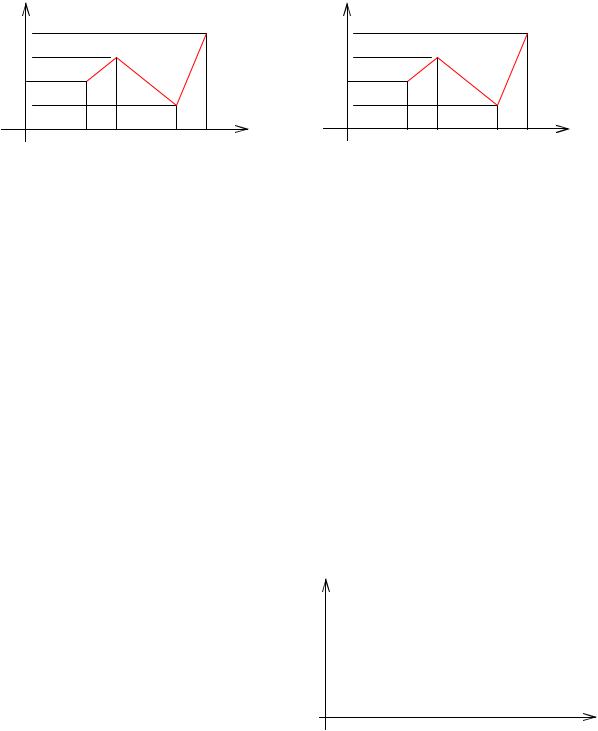
Полигоном частот называют ломаную, отрезки которой соединяют точки (x1; n1 ) , (x2 ; n2 ) , …, (xk ; nk ) .
Полигоном относительных частот называют ломаную, отрезки которой соединяют точки (x1; w1 ) , (x2 ; w2 ) , …, (xk ; wk ) .
Пример 3.
Дано распределение выборки
xi |
2 |
3 |
5 |
6 |
Σ |
ni |
10 |
15 |
5 |
20 |
50 |
Построить полигоны частот и относительных частот.
46
Решение. |
|
|
|
|
|
|
|
|
|
||||||||
ni |
ni |
||||||||||||||||
20 |
|
|
|
|
|
|
|
|
0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
15 |
|
|
|
|
|
|
|
|
0,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
10 |
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
5 |
|
|
|
|
|
|
|
|
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 3 4 5 6 xi |
|
|
1 2 3 4 5 6 xi |
||||||||||||
|
|
|
Полигон частот |
Полигон относительных частот |
|||||||||||||
В случае непрерывного признака целесообразно стоить гистограмму, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала ni – сумму частот вариант, попавших в i -ый
интервал.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы дли-
ной h , а высоты равны отношению nhi (плотность частоты). Аналогично оп-
ределяется гистограмма относительных частот.
Пример 4.
Построить гистограмму относительных частот по данному распределению выборки:
|
|
|
|
wi |
|
|
|
|
|
|
|
|
|
|
|
||||
Номер |
xi − xi +1 |
∑ni |
wi |
|
|
|
|
|
|
|
|
|
|
|
|||||
инт-ла |
|
частот |
h |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
10-15 |
2 |
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
15-20 |
4 |
0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3 |
20-25 |
8 |
0,4 |
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
4 |
25-30 |
4 |
0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
5 |
30-35 |
2 |
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
10 |
15 |
20 |
25 |
30 |
35 |
||||||||||||||
|
|
|
|
||||||||||||||||
Замечание. Площадь гистограммы частот равна сумме всех частот, т.е. объему выборки. Площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. 1.
