Гиперболическая парная зависимость

Параметры гиперболической зависимости у = а ₀ + b / х находятся по формулам:

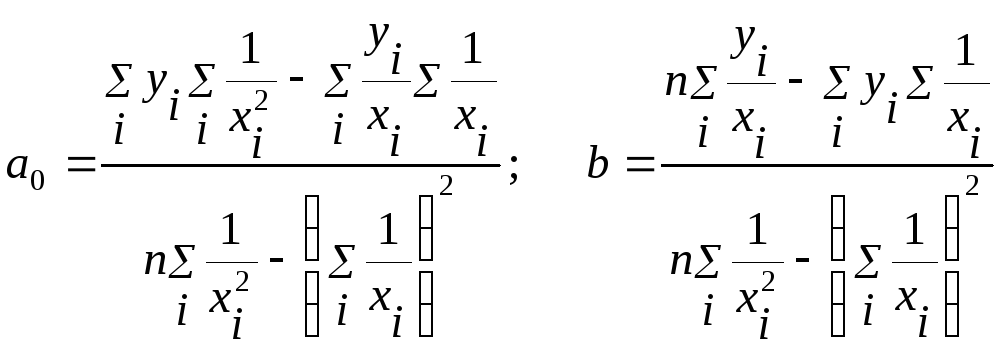
Полученная зависимость, также как и параболическая, проверяется расчетами индекса корреляции, критерия Стьюдента, критерия Фишера, и индекса детерминации.

Найдем гиперболические зависимости для тех же параметров, что и для параболы, между:

– выходной концентрацией и содержанием металла в руде (2–3):

у = 1,58 – 0,53 / х;

– содержанием металла в руде и извлечением (2–6):

у = 1,19 + 40,19 / х;

– содержанием металла в руде и хвосте (2–7):

у = –0,01 + 0,08 / х;

– выходной концентрацией и извлечением(3–6):

у = 2,04 + 42,63 / х;

– выходной концентрацией и содержание металла в хвосте(3–7):

у = 0,01 + 0,09 / х.

Рассчитываем значение дисперсии гиперболической зависимости (табл.7.3).

Таблица дисперсий и результаты оценки существенности

зависимости дисперсии	(2–3)	(2–6)	(2–7)	(3–6)	(3–7)
остаточная	0,002 5	138,63	0,001 74	239,65	0002
факторная	0,018	103,50	0,000 48	189,77	0,001
Общая	0,02	242,13	0,002 22	429,42	0,003
индекс корреляции	0,94	0,65	0,47	0,66	0,53
индекс детерминации	0,88	0,43	0,22	0,44	0,28
Tрасч	95,73	10,08	3,75	10,69	5,22
Tтабл	2,96	2,96	2,96	2,96	296
Fрасч	14,09	4,57	2,79	4,71	3,29
Fтабл	1,71	1,71	1,71	1,71	1,71

Поскольку для всех зависимостей t_расч > t_табл. и F_расч > F_табл, то все полученные индексы корреляции значимы и все гиперболические зависимости существенны. Все полученные уравнения адекватно описывают взаимодействие между параметрами.

В результате расчетов для одной пары показателей (у, х) были получены несколько статистически пригодных уравнений – линейная, параболическая и гиперболическая зависимости. Возникает задача выбора наилучшей формы зависимости для практического использования. Наилучшей формой зависимости признается та, для которой остаточная дисперсия принимает минимальное значение.

Для наглядности сведем в одну таблицу все остаточные дисперсии:

Зависимости Дисперсии	(2–3)	(2–6)	(2–7)	(3–6)	(3–7)
Остаточная дисперсия для линейной зависимости	0,001 7	8,090 1	0,000 20	7,150 9	0,000 3
Остаточная дисперсия для параболической зависимости	0,003 7	8,953 6	0,000 24	9,521 4	0000 8
Остаточная дисперсия для гиперболической зависимости	0,002 5	138,630 6	0,001 7	239,650 4	0,002 2

По приведенным в таблице данным видно, что для практического применения более пригодны все линейные зависимости, чем параболические или гиперболические зависимости.

Порядок выполнения работы

1. По предложенной методике изучить процедуру проведения однофакторного корреляционно-регрессионного анализа.

2. Построить линейную регрессионную парную зависимость.

3. Построить параболическую регрессионную парную зависимость.

4. Построить гиперболическую регрессионную парную зависимость.

5. Выбрать наилучшую форму зависимости на основе расчета критериев Стьюдента и Фишера, коэффициентов корреляции, используя лекционный материал.

Контрольные вопросы

1. Какие задачи ставит корреляционно-регрессионный анализ?

2. Какие процессы исследует корреляционно-регрессионный анализ,

3. Как выглядит линейная регрессионная модель?

4. На основании чего выбирается наилучшая форма зависимости, аппроксимирующая исходные данные?

5. Как рассчитывается среднеквадратичное отклонение одной переменной?

Лабораторная работа 8

Многофакторный корреляционный анализ

Цель работы: ознакомиться с порядком проведения многофакторного корреляционного анализа.

Проведение многофакторного корреляционного анализа

При проведении многофакторного корреляционного анализа необходимо учитывать возможность возникновения явления мультиколлениарности (явление «снежного кома»). Оно возникает тогда, когда в уравнение многофакторной зависимости включаются параметры (факторы) тесно связанные между собой. Чтобы этого избежать, в уравнения регрессии в качестве переменных должны включаться только независимые факторы. Если количество параметров x₁, x₂, … в исследовании невелико, то выделить независимые факторы можно с помощью критерия Стьюдента. Для этого:

1) составляется матрица парных коэффициентов корреляции, имеющая треугольную форму, поскольку r_{x1, x2} = r_{x2, x1};

2) для каждой пары факторов, которые включаются в уравнение, рассчитывается критерий Стьюдента t_расч = │r │ / (1 – r²) / √ (n – 1).

Если t_расч > t_табл., то связь признается существенной, и из двух выделенных факторов в уравнение регрессии должен включаться лишь один.

Для практических целей количество факторов в многофакторной модели не должно превышать 6–7.

Для построения модели используют метод стандартизированного масштаба. При этом на первом этапе получают не само уравнение регрессии, а его стандартизированный вид:

Коэффициенты β в этом уравнении позволяют перейти к натуральному масштабу, а кроме того, они показывают, на какую часть своего стандартного отклонения изменяется у, если х изменится на одно стандартное отклонение. Исходя из этого, β-коэффициенты считаются аналогом показателя устойчивости и позволяют определить те параметры, которые требуют особого контроля в автоматических системах управления или дополнительных приемов стабилизации.

Для построения уравнения в стандартизированном масштабе используется матрица парных коэффициентов корреляции. На ее основе составляется система нормальных уравнений. Количество уравнений и столбцов в ней зависит от числа неизвестных:

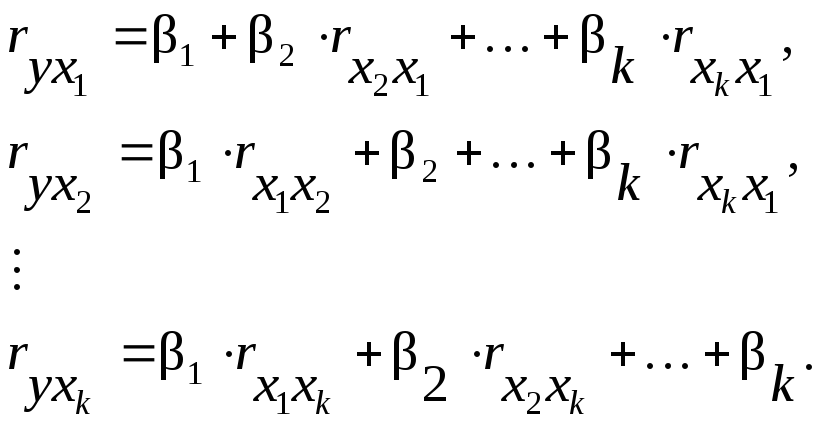
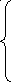
Стандартизированное уравнение переводится в натуральный масштаб, с помощью следующих формул:

;

;

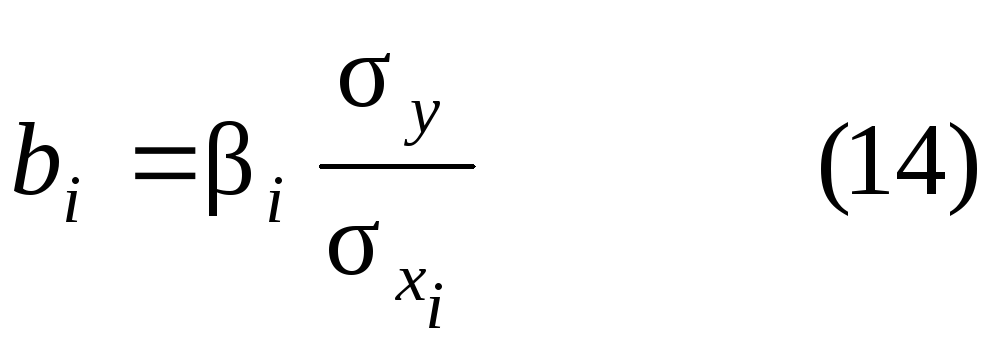y = b₀ + b₁x₁ + b₂x₁₂ + …

Полученное уравнение регрессии требуется оценить на значимость. Оценку производят следующим образом:

1. Определяется остаточная дисперсия

,

где К – число факторов.

2. Рассчитывается критерий Фишера F = σ² / σ_ост². Если F_расч > F_табл, то полученное уравнение хорошо описывает исследуемую зависимость. Чем больше критерий Фишера, тем более уравнение регрессии подходит для целей прогноза.

3. Рассчитывается коэффициенты множественной корреляции:

= √ (1 – σ_ост² / σ²).

4. Рассчитываются коэффициенты множественной детерминации R² .

5. Дополнительно рассчитывается среднеквадратичная ошибка коэффициента корреляции: S_k = (1 – R) / √ (N – k – 1).

6. Определяется существенность коэффициента множественной корреляции: t_расч. = R / S_k. Если t_расч > t_табл, то коэффициент множественной корреляции считается существенным.

Составим по этим правилам матрицу расчетных критериев Стьюдента для всех 8 исследуемых факторов х₁, х₂, …, х₈, сведенные в приведенную ниже таблицу:

	x1	x2	x 3	x4	x5	x6	x7	x8
x1	1	3,6757	2,6550	0,0280	0,5173	1,0478	2,5745	0,1641
x2	3,6757	1	62,2734	1,4791	0,2527	2,6270	10,8963	1,1329
x3	2,6550	62,2734	1	2,2296	0,0805	3,7414	6,4842	1,6404
x4	0,0280	1,4791	2,2296	1	1,5261	1,5071	0,4652	1,6365
x5	0,5173	0,2527	0,0805	1,5261	1	0,3673	0,3721	0,6368
x6	1,0478	2,6270	3,7414	1,5071	0,3673	1	1,2997	5,4576
x7	2,5745	10,8963	6,4842	0,4652	0,3721	1,2997	1	0,7004
x8	0,1641	1,1329	1,6404	1,6365	0,6368	5,4576	0,7004	1

Проверка на существенность и отсев второстепенных факторов производится сравнением с табличным значением t_табл = 1,71. Если связь признается существенной, то из двух выделенных факторов в уравнение регрессии должен включаться лишь один. После этого можно строить многофакторную зависимость. Построим следующие две многофакторные модели (см. табл. 1 приложения):

1. Зависимость количества переработанной руды (1) от содержания металла в руде (2), содержания металла в концентрате (4), содержание серы в концентрате (5), извлечения (6).

Стандартизированный вид уравнения:

у₁⁰ = β₁ х₂⁰ + β₂ х₄⁰ + β₃ х₅⁰ + β₄ х₆⁰ =

= –0,418 х₂⁰ + 1,014х₄^{0 –} 1,339 х₅⁰ + 1,115 х₆⁰.

Уравнение в натуральном масштабе:

y₁ = b₀ + b₁ x₂ + b₂ x₄ + b₃ x₅ + b₄x₆ =

= 1136,08 – 122,97х₂ + 529,16х₄ – 17,92х₅ + 2034,78х₆.

Проведем оценку значимости уравнения многофакторной регрессии:

Остаточная дисперсия	11144,17
Расчетное значение критерия Фишера Fрасч	0,16
Коэффициент множественной корреляции	0,35
Коэффициент множественной детерминации	0,125
Среднеквадратичная ошибка корреляции Sk	0,168
Расчетное значение критерия Стьюдента tрасч	2,14
Табличное значение критерия Стьюдента tтабл.	1,70
Существенность коэффициента множественной корреляции	2,098

Сравнивая табличное значение критерия Стьюдента с расчетным значением, можно сделать вывод о том, что коэффициент множественной корреляции существенен. Однако значение критерия Фишера F_расч = 0,16 очень мало, значит, данное уравнение нельзя использовать на практике для планирования и проектирования АСУТП. В то же время, хотя уравнение плохо описывает реальный процесс, его можно использовать для анализа.

2. Зависимость извлечения (6) от количества перерабатываемой руды (1), содержания металла в руде (2), содержания металла в хвосте (7), содержания металла в сульфате (8).

Стандартизированный вид уравнения:

у₆⁰ = β₁ х₁ ⁰ + β₂ х₂⁰ + β₃ х₇⁰ + β₄ х₈⁰ = 0,004 4 х₁⁰ + 1,368х₂⁰ +

+ 1,272 х₇⁰ + 1,181 х₈⁰.

Уравнение в натуральном масштабе:

у = 55,31 + 0,0003х₁ + 43,27х₂ – 37,34х₇ + 2,78х₈.

Проведем оценку значимости уравнения многофакторной регрессии:

Остаточная дисперсия	10,099
Расчетное значение критерия Фишера Fрасч	0,993
Коэффициент множественной корреляции	0,855
Коэффициент множественной детерминации	0,7307
Среднеквадратичная ошибка корреляции Sk	0,052
Расчетное значение критерия Стьюдента tрасч	16,49
Табличное значение критерия Стьюдента tтабл.	1,70

Табличное значение критерия Стьюдента значительно меньше расчетного, t_расч > t_табл., отсюда можно сделать вывод о том, что коэффициент множественной корреляции существенен. Значение критерия Фишера F_расч = 0,993 больше по сравнению со значением критерия Фишера для первой рассмотренной зависимости, значит, последняя зависимость является более пригодной для прогноза.

В то же время, поскольку значение критерия Фишера мало, его нельзя использовать на практике для планирования и проектирования АСУТП, поскольку зависимость плохо описывает реальный процесс.