3. Метод Нелдера-Мида (метод деформируемого многогранника)

Чтобы можно было оценить метод Нелдера -Мида, кратко рассмотрим поиск по регулярному многограннику, предложенный Спендли, Хекстом и Химсвортом.

Регулярным многогранником (симплексом) в n-мерном пространстве называется множество из (n+1)-ой равноудалённой точки. На плоскости симплексом является равносторонний треугольник, в пространстве - правильный тетраэдр.

Из аналитической геометрии известно, что координаты вершин регулярного симплекса определяются следующей матрицей D размерности :

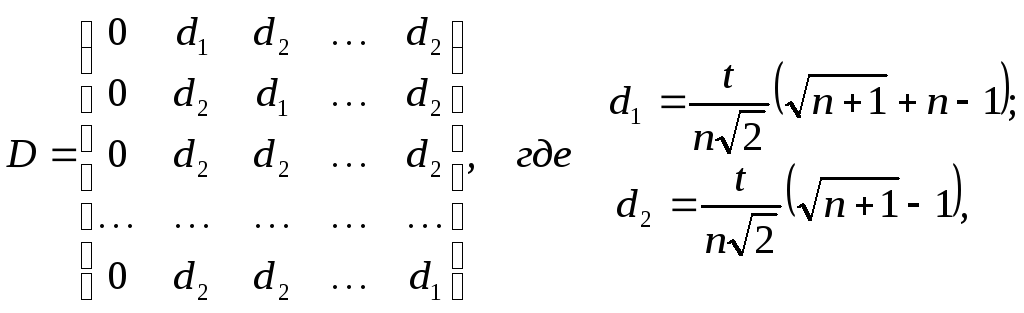
где t - расстояние между двумя вершинами. Столбцы этой матрицы являются координатами вершин симплекса.

При оптимизации этим методом целевая функция вычисляется в каждой вершине регулярного симплекса. Из вершины, где целевая функция максимальна, проводится проектирующая прямая через центр тяжести симплекса, затем вершина с максимальным значением функции отбрасывается и строится новый (отражённый) симплекс из оставшихся прежних точек и одной новой точки, расположенной на проектирующей прямой на надлежащем расстоянии от центра тяжести. Продолжение этой процедуры, в которой каждый раз отбрасывается точка с максимальным значением целевой функции, а также использование правил уменьшения размера симплекса и предотвращения циклического движения в окрестности экстремума позволяют осуществить поиск, в котором величина шага на любом этапе фиксирована, а направление поиска можно менять (производные не используются).

Последовательные симплексы, построенные в двумерном пространстве для минимизации «хорошей» целевой функцией, приведены на рис. 8.

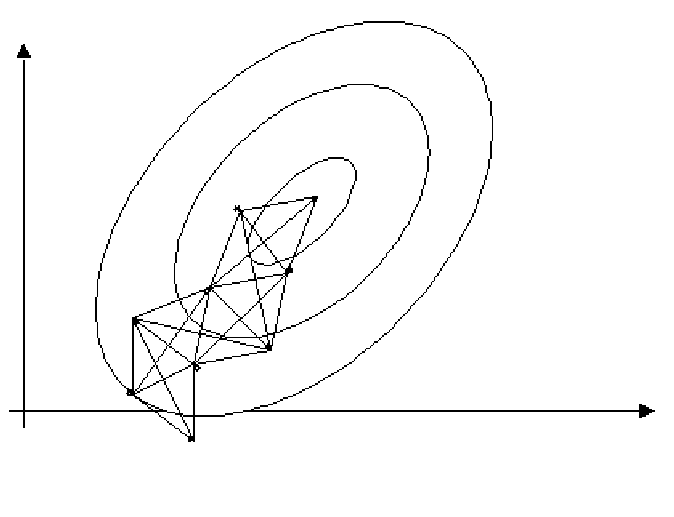
Рис. 8

Определённые трудности, встречающиеся при использовании этого метода, а именно отсутствие ускорения поиска в «хорошем направлении» и трудности при поиске на искривлённых «оврагах» и «хребтах» привели к необходимости модификаций алгоритма.

Нелдер и Мид (1964) предложили модификацию, в которой симплекс может изменять свою форму. Так как в этом случае симплекс уже не будет регулярным, метод назвали поиском по деформируемому многограннику.

Обсудим этот метод. Минимизируется функция n независимых переменных с использованием (n+1) вершин многогранника. Вершина, в которой значение функции наибольшее, проектируется через центр тяжести оставшихся вершин. Улучшенные значения целевой функции находятся последовательной заменой точки с наибольшим значением на более «хорошие» точки, пока не будет найден минимум. При этом многогранник может вытягиваться или сжиматься по выбранному направлению.

Пусть являются i-ой вершиной на некотором k-ом этапе поиска. Пусть также

,

т.е. в точке функция принимает наибольшее значение, а в точке- наименьшее значение среди точек многогранника.

Так как многогранник состоит из точек, то центр тяжести всех вершин, кроме, обозначим через. Координатыопределяются по формуле

.

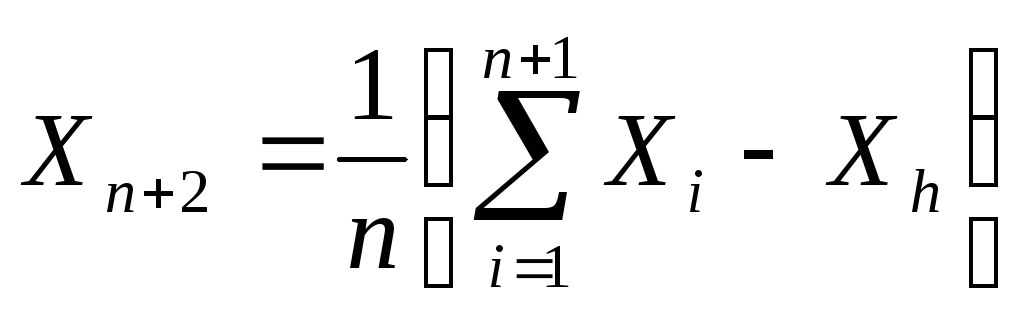Начальный многогранник обычно выбирается в виде регулярного симплекса (но это не обязательно) с точкой 1 в качестве начала координат. Начало координат может быть также помещено в центре тяжести многогранника.

Алгоритм деформируемого многогранника состоит из операций отражения, растяжения, сжатия и редукции.

Отражение. Вершина проектируется через центр тяжести оставшихся вершин в соответ­ствии с соотношением

,

где α > 0 является коэффициен­том отражения (рис.9). Первой всегда выполняется операция отражения.

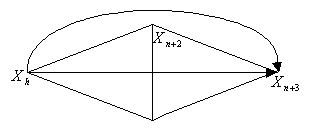
Рис. 9

Растяжение. Если , то векторрастягивается в соответствии с соотношением

,

где γ>1 - коэффициент растяжения (рис 10).

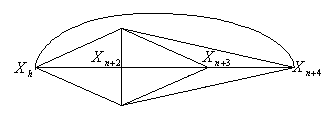
Рис. 10

Если , тозаменяется наи процедура продолжается снова с операции отражения.

В противном случае заменяется наи также осуществляется переход к операции отражения.

Сжатие. Если для всех, то векторсжимается в соответствии с формулой

,

где 0 < β < 1 – коэффициент сжатия (рис. 11).

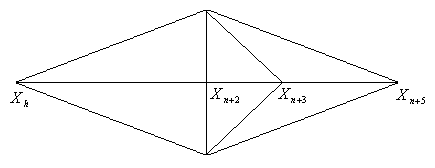
Рис. 11

Затем заменяется наи осуществляется переход к операции отражения для продолжения поиска.

Редукция. Если , то все векторыуменьшаются в 2 раза с отсчетом отв соответствии с формулой

.

Затем алгоритм возвращается к операции отражения для продолжения поиска на следующем шаге.

Если ни одна из операций (растяжение, сжатие, редукция) не выполняется, происходит операция отражения.

Критерий окончания поиска, предложенный Нелдером и Мидом записывается в виде формулы

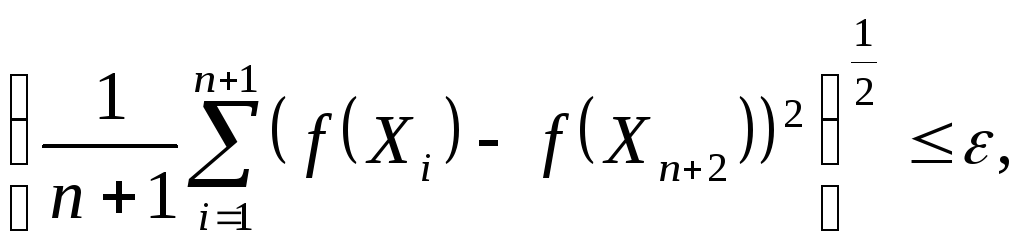
где ε - произвольное малое число, - центр тяжести многогранника на данном шаге.

Деформируемый многогранник в противоположность жёсткому симплексу адаптируется к топографии целевой функции, вытягиваясь вдоль длинных наклонных плоскостей, изменяя направление в изогнутых впадинах и сжимаясь в окрестности минимума, что достигается выбором коэффициентов сжатия, растяжения и отражения.

Как следует выбирать α, β и γ ?

После того как деформируемый многогранник подходящим образом промасштабирован, его размеры должны поддерживаться неизменными, пока изменения в топологии задачи не потребуют применения многогранника другой формы. Это можно реализовать только при α =1. Было показано, что при α < 1 требуется большее количество вычислений целевой функции. Если α >>1, то это затрудняет адаптацию многогранника при изменениях направления поиска и замедляет сходимость в окрестности минимума. Таким образом, α =1 выбирается как компромисс. Чтобы выяснить, какое влияние на поиск имеет выбор β и γ, были проведены решения тестовых задач. Оказалось, что влияние β на эффективность поиска, более заметно, чем влияние γ.

Для практических нужд Нелдером и Мидом были рекомендованы следующие значения коэффициентов: α = 1, β = 0,5, γ = 2.