
- •Предисловие
- •1.1. Постановка и классификация задач
- •1.2. Основные определения
- •1.3. Классический метод определения экстремума функции
- •Контрольные вопросы и задания
- •Глава 2. Одномерная оптимизация
- •2.1. Интервал неопределенности
- •2.2. Метод дихотомии
- •2.3. Метод фибоначчи
- •2.4. Метод золотого сечения
- •2.5. Метод квадратичной интерполяции
- •Контрольные вопросы и задания
- •Глава 3. Оптимизация функций нескольких переменных
- •3.1. Методы прямого поиска
- •3.1.1. Метод покоординатного спуска
- •3.1.2. Метод поиска Хука – Дживса
- •Метод Розенброка (метод вращающихся координат)
- •Метод Нелдера-Мида (метод деформируемого многогранника)
- •Метод сопряженных направлений Пауэлла
- •3.1.6. Методы случайного поиска
- •3.2. Градиентные методы
- •3.2.1. Метод наискорейшего спуска
- •Метод сопряженных градиентов Флетчера и Ривса
- •3.3. Методы второго порядка
- •3.3.1. Метод Ньютона
- •3.3.2.Метод Дэвидона - Флетчера - Пауэлла
- •Итерационная процедура Дэвидона-Флетчер-Пауэлла может быть представлена последовательностью шагов.
- •Контрольные вопросы и задания
- •Глава 4. Условная оптимизация
- •4.1. Множители лагранжа
- •4.2. Условия куна - таккера
- •Методы решения задач условной оптимизации
- •4.3.1. Метод последовательной безусловной оптимизации
- •4.3.2.Метод скользящего допуска
- •Контрольные вопросы и задания
- •Глава 5. Линейное программирование
- •5.1. Постановка задачи лп
- •Тогда задача лп (1) - (3) запишется в виде
- •5..2. Каноническая и стандартная формы задачи лп
- •5.3. Симплекс - метод
- •Порождение начального допустимого базисного решения
- •Двойственность в линейном программировании
- •5.6. Транспортная задача
- •Контрольные вопросы и задания
- •Заключение
- •Библиографический список
- •Глава1. Безусловная оптимизация………..………4
- •Глава 2. Одномерная оптимизация………..….…….9
- •Глава 3. Оптимизация функций нескольких переменных………………………………………..….…..20
- •Глава 4. Условная оптимизация…………………..49
- •Глава 5. Линейное программирование…………..60
- •Лидия Ивановна Лыткина Методы оптимизации с программами в системе mathcad
- •660014, Красноярск, просп. Им. Газ. ”Красноярский рабочий”, 31.
Глава 2. Одномерная оптимизация
Задача оптимизации, в которой целевая функция задана функцией одной переменной, относится к наиболее простому типу оптимизационных задач. Тем не менее анализ задач такого типа занимает важное место в оптимизационных исследованиях, как теоретической так и практической направленности. Это связано с тем, что одномерные методы оптимизации часто используются при решении задач с несколькими переменными при подходящем выборе направления и последующей минимизации вдоль этого направления. Для решения задач одномерной оптимизации в этой главе рассматриваются методы дихотомии, золотого сечения, Фибоначчи, квадратичной интерполяции.
2.1. Интервал неопределенности
Пусть
требуется решить следующую задачу:
min
f(x),
![]() .
.
С
помощью численных методов можно
определить минимум функции на некотором
интервале
![]() ,
называемым интервалом неопределенности.
Будем предполагать, что на интервале
неопределенности функция f(x)
унимодальна. Для решения этой задачи
могут быть использованы два подхода:
,
называемым интервалом неопределенности.
Будем предполагать, что на интервале
неопределенности функция f(x)
унимодальна. Для решения этой задачи
могут быть использованы два подхода:
-сокращение интервала неопределенности;
-аппроксимация функции.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рис. 1 Рис. 2
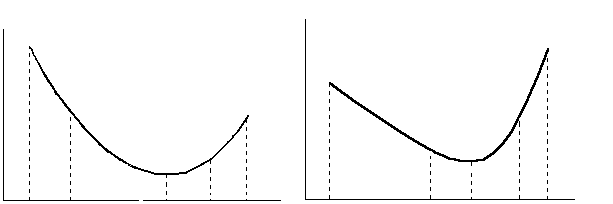
Следующая теорема позволяет сократить интервал неопределенности.
Теорема.
Пусть функция
f
унимодальна
на замкнутом интервале![]()
![]() ,
а ее минимум достигается в точке
,
а ее минимум достигается в точке![]() .
Рассмотрим точки
.
Рассмотрим точки![]() и
и![]() ,
расположенные в интервале таким образом,
что
,
расположенные в интервале таким образом,
что![]() .
Сравнивая значения функции в точках
.
Сравнивая значения функции в точках![]() и
и![]() ,
можно сделать следующие выводы:
,
можно сделать следующие выводы:
Если
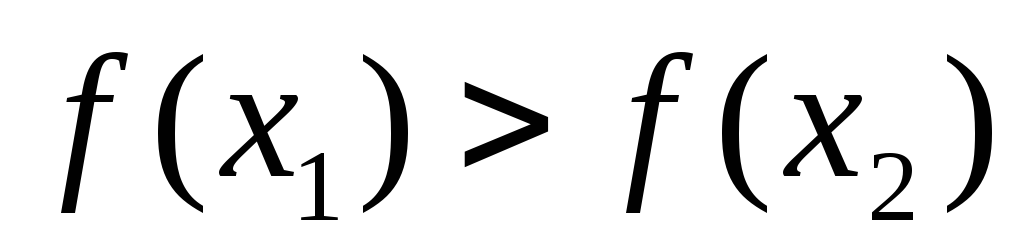 ,
то точка минимума
,
то точка минимума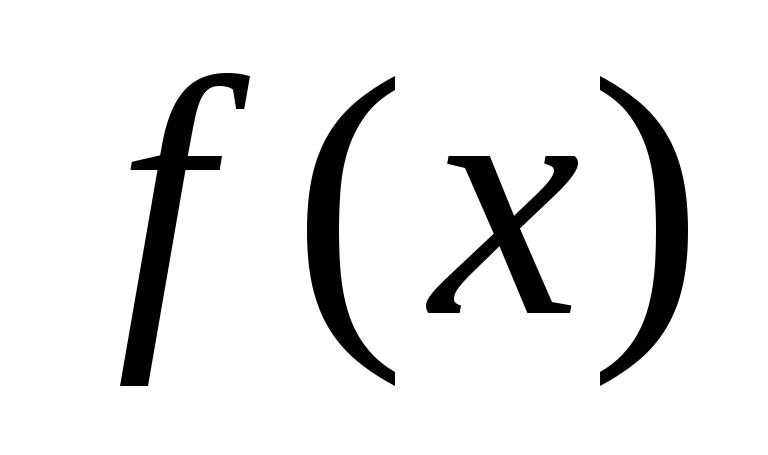 не лежит в интервале
не лежит в интервале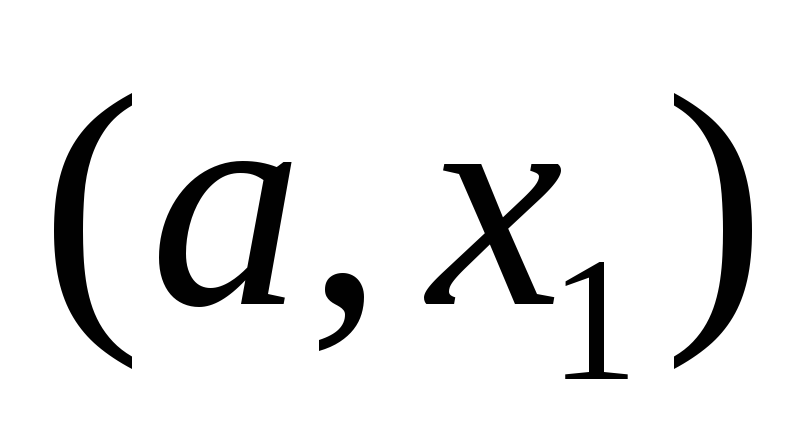 ,
т.е.
,
т.е. (рис. 1).
(рис. 1).Если
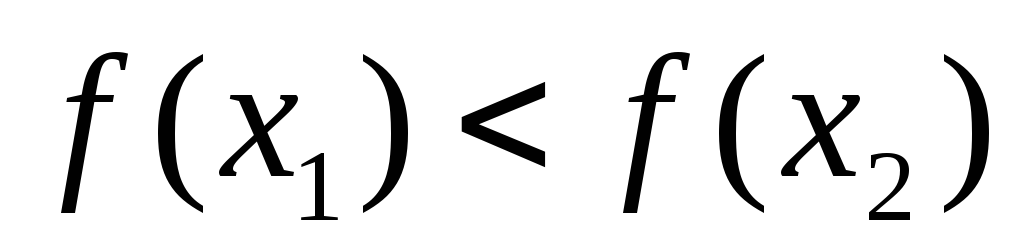 ,
то точка минимума не лежит в интервале
,
то точка минимума не лежит в интервале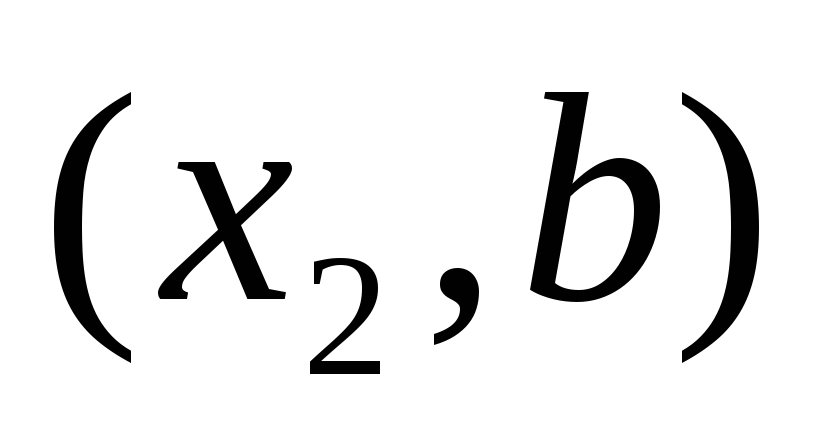 ,
т.е.
,
т.е.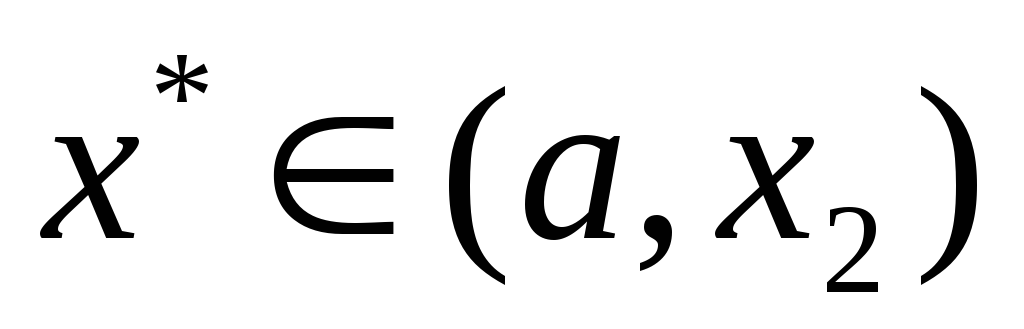 (рис. 2).
(рис. 2).
Примечание.![]() Если
Если![]()
![]() ,
то можно исключить оба крайних интервала
,
то можно исключить оба крайних интервала![]() и
и![]() ;
при этом точка минимума должна
располагаться в интервале
;
при этом точка минимума должна
располагаться в интервале![]() .
.
Результаты этой теоремы используются при сокращении интервала неопределенности методами дихотомии, золотого сечения, Фибоначчи.
2.2. Метод дихотомии
Метод
дихотомии позволяет сократить интервал
неопределенности почти в два раза на
каждой итерации, при этом целевая
функция вычисляется только в двух
точках. Если функцию можно вычислить
в
![]() точках,
то длина интервала неопределенности
может быть сокращена в
точках,
то длина интервала неопределенности
может быть сокращена в
![]() раза.
раза.
Идея
этого метода заключается в следующем:
точки
![]() и
и![]() выбираются симметрично на расстоянии
выбираются симметрично на расстоянии![]() от середины
от середины![]() .
В зависимости от значений функций в
точках
.
В зависимости от значений функций в
точках![]() и
и![]() на следующем этапе в качестве интервала
неопределенности выбирается либо
на следующем этапе в качестве интервала
неопределенности выбирается либо![]() ,
либо
,
либо![]() (см.
теорему сокращения интервала
неопределенности).
(см.
теорему сокращения интервала
неопределенности).
Алгоритм.
Пусть
функция
![]() унимодальна на интервале
унимодальна на интервале![]() .
.
1.
Начальный
шаг. Выбирается
положительное малое
![]() и
и![]() .
Положим
.
Положим![]()
![]() .
.
2. Основной шаг:
а)
если
![]() ,
то
,
то![]() и вычисления прекращаются; если
и вычисления прекращаются; если![]() ,
то определяются величины
,
то определяются величины
![]() ;
;
![]() ,
,
и переходим к пункту b);
b)
если
![]() ,
то
,
то![]() ,
,![]() .
В противном случае
.
В противном случае![]() ,
,![]() .
После этого
.
После этого![]() и осуществляется переход к пунктуa).
и осуществляется переход к пунктуa).
Пример. Щелкнув по значку, откроется Mathcad - документ метода дихотомии, в котором можно выполнить вычисления.

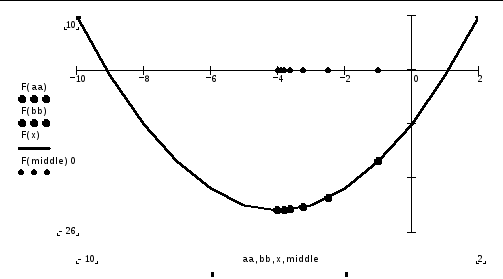
Минимизация
функции
![]() методом дихотомии
методом дихотомии
Если
![]() - длина конечного интервала неопределенности,
то минимальное числоn
вычислений значений функции, необходимых
для достижения заданной точности, можно
найти по условию
- длина конечного интервала неопределенности,
то минимальное числоn
вычислений значений функции, необходимых
для достижения заданной точности, можно
найти по условию
![]() .
.
