2.3. Метод фибоначчи

Метод дихотомии не эффективен в том смысле, что для конечного фиксированного числа вычислений значений функции , он не приводит к наименьшему возможному интервалу. Эффективным методом в этом смысле является метод Фибоначчи.

Важнейшая особенность этого метода состоит в том, что он позволяет для заранее заданного числа вычислений функции построить оптимальную процедуру поиска минимума унимодальной функции.

Предположим, что заданный начальный интервал неопределенности ,является интервалом неопределенности, полученным после-той итерации. Рассмотрим две точкиииз интервала, заданные с помощью соотношений

,

,

где - заданное число вычислений функции;- последовательность чисел Фибоначчи, заданная с помощью рекуррентной формулы

, где .

Новый интервал неопределенности равен, если, и равен, если. Тогда в первом случае, новый интервал неопределенности имеет длину

а во втором

Отсюда следует, что в любом случае на -той итерации интервал неопределенности сжимается враз. На-той итерации либо, либоПоэтому на каждом шаге вычисляется только одно новое значение функции. На (n-1)-ой итерации и значение функции не вычисляется.

Если есть точность вычисления значения функции,- максимально возможное число вычислений функции, то конечный интервал неопределенности будет равен

,

т.е. сократится в раз.

Пример. Щелкнув по значку, откроется Mathcad - документ метода Фибоначчи, в котором можно выполнить вычисления.

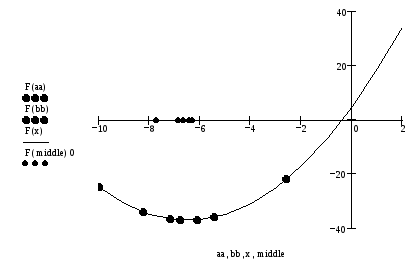
Минимизация функции методом Фибоначчи

2.4. Метод золотого сечения

Не всегда можно определить заранее, сколько раз придется вычислять функцию. Метод золотого сечения почти столь же эффективен при , что и метод Фибоначчи, однако при этом не требуется знать- количество вычислений функции.

Сущность этого метода заключается в следующем. Интервал неопределенности делится на две неравные части так, что отношение длины большего отрезка к длине всего интервала равно отношению длины меньшего отрезка к длине большего (рис 3).

,

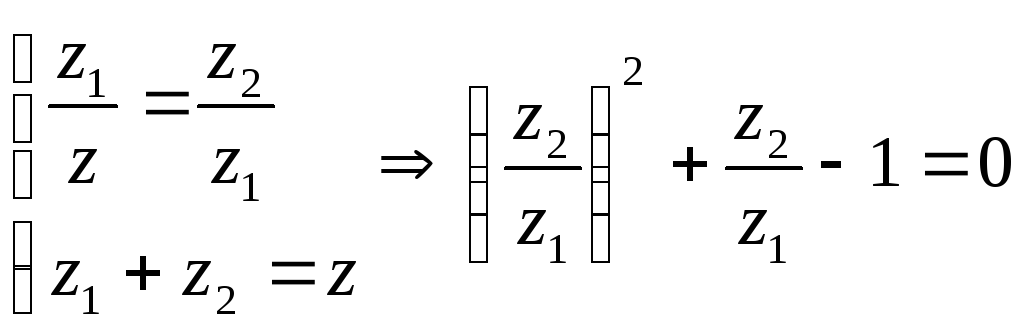
где - “золотое сечение”.

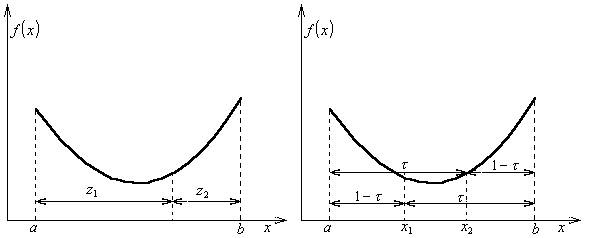
Рис. 3 Рис.4

На каждом шаге этой итеративной процедуры, кроме первого, вычисляется только одно значение функции. Однако Химмельблау рекомендовал вычислять на каждом шаге две точки, для того чтобы не накапливалась погрешность, так как имеет приближенное значение (рис 4).

Если длина конечного интервала неопределенности равна , то для достижения требуемой точности число вычислений значений функции по методу золотого сечения можно найти по условию

.

Алгоритм.

1. Начальный этап. Пусть 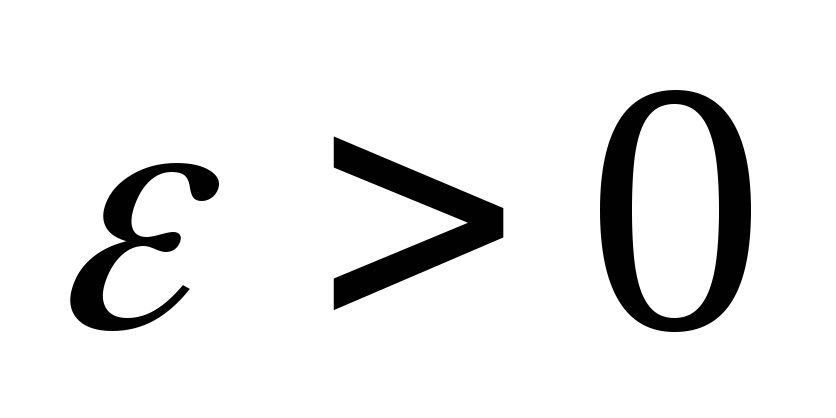- заданная точность. Положим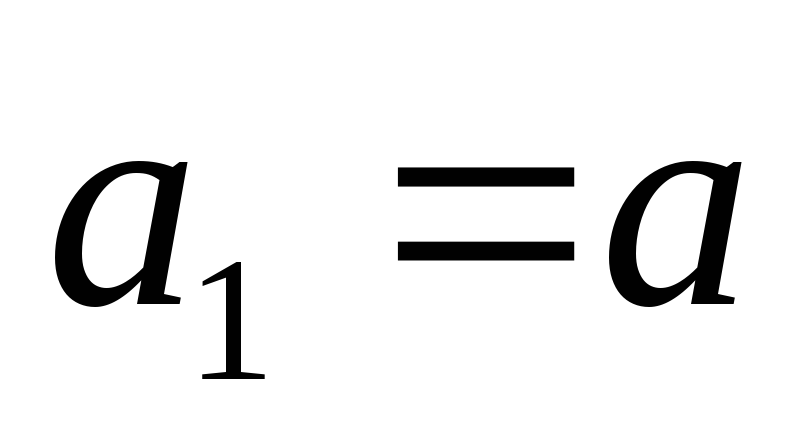; 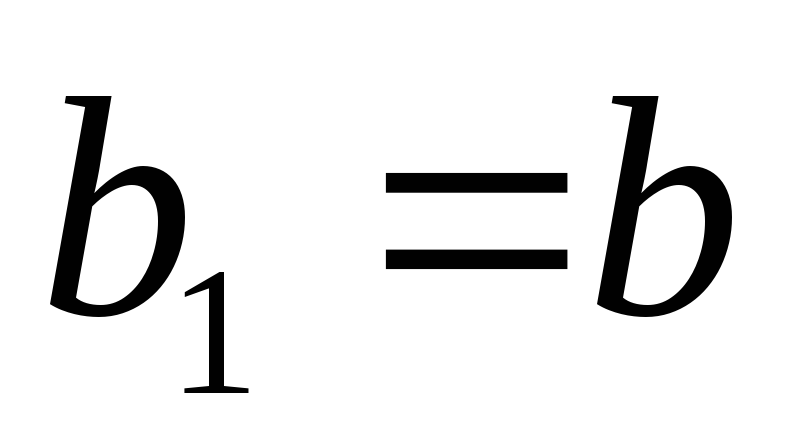. Вычислим

где ,.

Вычислим и. Пусть.

2. Основной этап:

a) если , тои вычисления закончить; в противном случае, если, то перейти к шагу b);

если , то перейти к шагу c);

b) примем ,,,

; вычислим и перейдем к шагуd);

c) ,,,; вычислими перейдем к

шагу d);

d) и перейдем к шагу a).

Существует другой подход к определению минимума функции одной переменной. Целевую функцию можно аппроксимировать полиномом степени . Один из них рассматривается ниже.

Пример.Щелкнув по значку, откроется Mathcad - документ метода золотого сечения, в котором можно выполнить вычисления.

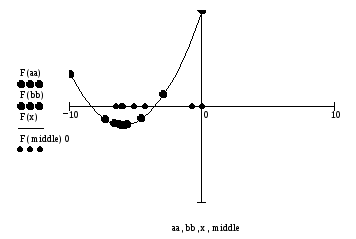Минимизация функции

методом золотого сечения