5.6. Транспортная задача

Рассмотрим частный случай задачи ЛП - транспортную задачу.

Имеется m пунктов производства с объемами производства и n пунктов потребления с объемами потребления . Если- это стоимость транспортировки одного изделия (единицы продукции) из пункта производства i в пункт потребленияj, то задача заключается в планировании перевозок от поставщиков к потребителям, минимизирующих стоимость транспортировки.

Построим математическую модель: пусть является объемом планируемой перевозки продукции от поставщика i к потребителю j. Тогда сформулированную задачу можно записать в виде задачи ЛП:

при ограничениях

;

;

………………………………………………………..

;

;

………………………………………………………

;

,

или (в краткой форме записи)

при ограничениях

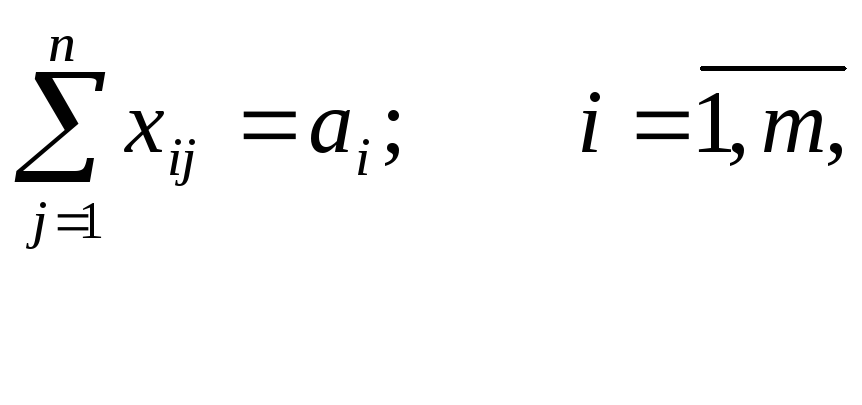
Если в транспортной задаче выполняется условие , то она называется задачей закрытого типа. Транспортная задача закрытого типа всегда имеет решение. Если в транспортной задаче суммарные запасы не совпадают с суммарными потребностями (), то она называется задачей открытого типа.

Транспортная задача открытого типа решается приведением к задаче закрытого типа, для чего вводится фиктивный поставщик или фиктивный потребитель, в зависимости от того, что превышает: суммарные потребности или суммарные запасы.

Стоимость перевозки единицы продукции от фиктивного поставщика или до фиктивного потребителя полагается равной нулю, т.е. груз в обоих случаях не перевозится.

Транспортная задача является частным случаем задачи ЛП и может быть решена симплекс-методом, но он не эффективен в данном случае. Матрица ограничений имеет специальный вид: все элементы матрицы - это нули или единицы, причем они расположены с некоторой закономерностью. Поэтому для транспортной задачи были предложены более эффективные методы.

Решение транспортной задачи выполняется в специальной таблице (табл. 3), называемой матрицей планирования. В нее заносятся исходные данные задачи.

Таблица 3

Решение состоит из двух этапов: первый - построение первоначального допустимого базисного решения, которое определяется методом минимальной стоимости по правилу: самая дешевая продукция реализуется первой; второй этап - проверка решения на оптимальность и переход к новому базисному решению (метод потенциалов).

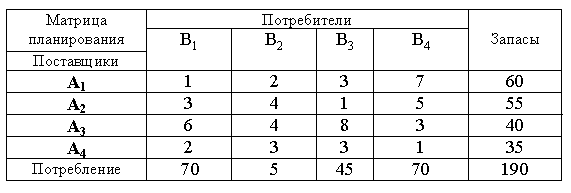
Пример. Решить транспортную задачу, исходные данные которой записаны в табл. 4.

1 этап. Определим начальное допустимое базисное решение (табл.4 На каждом шаге следует выбирать клетку, отвечающую минимальной стоимости транспортировки. Выбираем клетку с минимальной стоимостью - это (A₁,B₁). Если таких клеток несколько, то берем

Таблица 4

первую по порядку. В выбранную клетку заносим меньшее из чисел a_i или b_j ( в данном случае 60 ), т.е. запасы поставщика А₁ полностью переходят к потребителю В₁, частично удовлетворяя его потребности. Остальные клетки выбранной строки или столбца прочеркиваем. Процесс продолжается до тех пор, пока все клетки не будут прочеркнуты или заняты (табл.5).

Таблица 5

2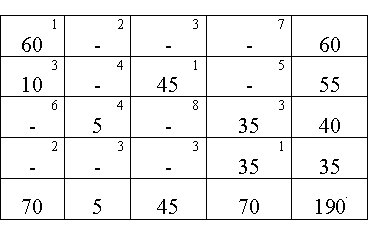этап. Проверяем полученное решение на оптимальность, для чего строим систему потенциалов. Система потенциалов строится по следующим правилам:

для занятых клеток;

для свободных клеток.

Выбираем строку (или столбец) с наибольшим числом занятых клеток (3-я строка) и приравниваем потенциал нулю (). Для занятых клеток этой строки находим второй потенциал из соотношения(). Используя полученные потенциалыдля занятых клеток, находим потенциалыи т.д. В нашем примере дальнейшее построение потенциалов прерывается, поскольку для каждой занятой клетки либо известны оба потенциала, либо не известен ни один. Это произошло потому, что построенное на первом этапе решение является вырожденным.

Таблица 6

Невырожденное базисное решение содержит отличных от нуля компонент. Если базисное решение вырожденное, то вводится недостающее число занятых клеток с нулевыми объемами перевозок.

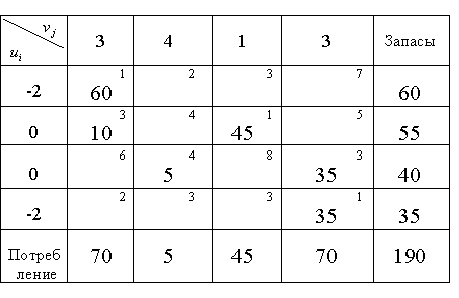
Необходимо ввести одну фиктивно занятую клетку такую, для которой известен один и только один потенциал (желательно с минимальной стоимостью).

Выбираем клетку , записываем в нее нуль (объем перевозки) и в дальнейшем рассматриваем ее как занятую. Теперь с помощью фиктивно занятой клетки находим остальные потенциалы (табл. 5). После построения системы потенциалов проверяем свободные клетки на оптимальность.

Для всех свободных клеток условие выполнено. Следовательно базисное решение, записанное в матрице планирования является оптимальным :

,

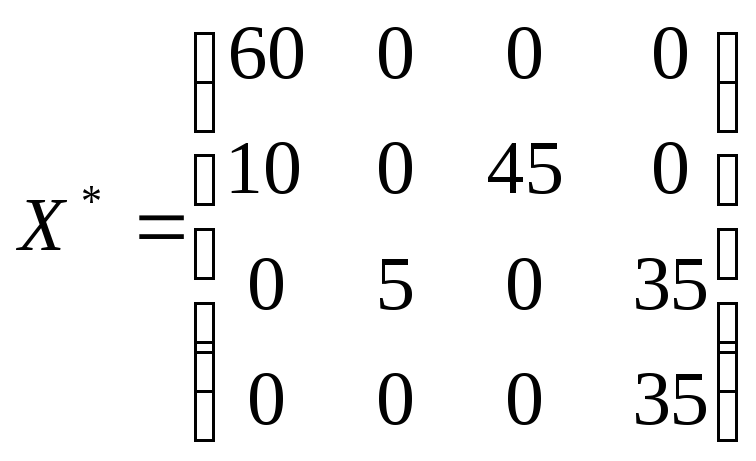Если условие не выполнено хотя бы для одной свободной клетки, то необходимо построить другое базисное решение, т.е. перераспределить объемы перевозок (пример 2).

Пример 2. Пусть для некоторой транспортной задачи построено начальное базисное решение и система потенциалов. (табл. 7) Условие оптимальности не выполнено для клетки . В эту клетку в правый нижний угол записываем разность. Клетку делаем условно занятой (+). Если клеток с нарушением условия оптимальности несколько, то занятой делаем ту, в которой разность- максимальна.

Перераспределение груза происходит по циклу. Цикл – замкнутая ломаная линия, вершины которой расположены в занятых клетках таблицы, а звенья вдоль строк и столбцов.

Цикл строится, начиная с клетки, помеченной плюсом, и следующие вершины цикла помечаем поочередно –(минус) и +(плюс). Затем находим величину (количество перераспределенного груза), равную минимальному объему перевозки в клетках цикла, отмеченных знаком минус (табл. 7):

.

Значение записываем в помеченную знаком +(плюс) незанятую клетку цикла. Далее, двигаясь по циклу, вычитаемиз объемов перевозок в “минусовых” клетках и прибавляем к объемам перевозок в “плюсовых” клетках. Клетку цикла, в которой объем перевозок

Таблица 7

стал равным нулю делаем незанятой (если клеток с нулевой перевозкой имеется несколько, то незанятой делаем только одну из них). Полученное решение нужно проверить на оптимальность, причем для этого нет необходимости строить заново всю систему потенциалов. Достаточно внести лишь некоторые исправления в систему потенциалов предыдущего решения, начиная с клетки (табл. 8).

Условия оптимальности выполняются. Получено оптимальное решение:

,

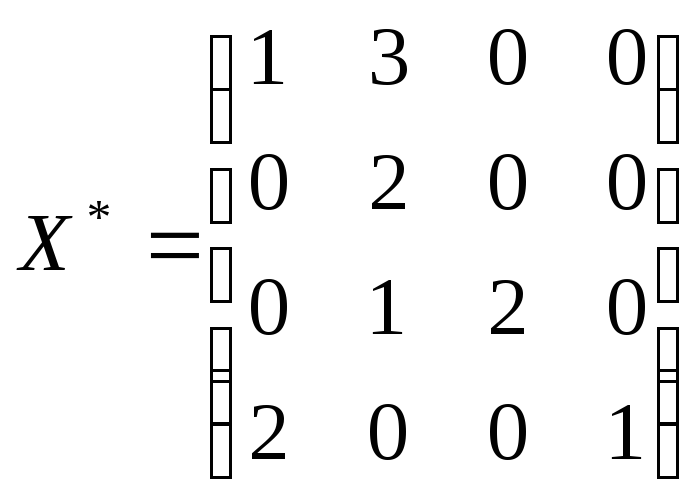Таблица 8

Таким образом, алгоритм, предложенный Данцигом в 1947 г. до сих пор продолжает с успехом применяться. Его суть состоит в переходе от одного базисного решения к другому, пока не будет достигнуто оптимальное значение функции.

Транспортная задача, которая является частным случаем задачи ЛП, имеет широкое практическое значение.