Итерационная процедура Дэвидона-Флетчер-Пауэлла может быть представлена последовательностью шагов.

Шаг 1. Выбирается -начальная точка поиска и- положительно определенная симметрическая матрица;.

Шаг 2. В качестве направления поиска выбирается .

Шаг 3. Вычисляется , гдеопределяется из условия.

Шаг 4. Если , то минимум найден; в противном случае выполняется шаг 5.

Шаг 5. Вычисляются ипо формулам (1) - (4).

Шаг 6. . Повторяется шаг 2.

Следует отметить, что в случае квадратичной функции процедура Дэвидона-Флетчера-Пауэлла использует сопряженные направления и минимум определяется за шагов. Этот метод является эффективным и для нелинейных функций общего вида.

Однако алгоритм Дэвидона-Флетчера-Пауэлла может привести к ситуации, когда матрица становится плохо обусловленной или же нарушается условие положительной определенности. Причиной этого может быть неудачный выбор начального приближения, а также наличие ошибок округления. Для преодоления этих трудностей следует повысить точность вычислений и периодически обновлять итерационный процесс.

Метод Дэвидона-Флетчера-Пауэлла является наиболее широко используемым. Он отличается устойчивостью и успешно применяется при решении самых различных задач.

Итак, хотя нет ни одного универсального метода, позволяющего успешно решать все задачи, некоторые методы лучше приспособлены для решения задач определенного типа. Тщательный выбор подходящего алгоритма часто позволяет сэкономить и машинное время, и усилия, затрачиваемые инженером на решение задачи. В главе даны рекомендации какие алгоритмы предпочесть, для чего рассмотрены методы прямого поиска, градиентные методы и методы второго порядка.

Пример. Щелкнув по значку, откроется Mathcad документ метода Дэвидона-Флетчера-Пауэллав, в котором можно выполнить вычисления.

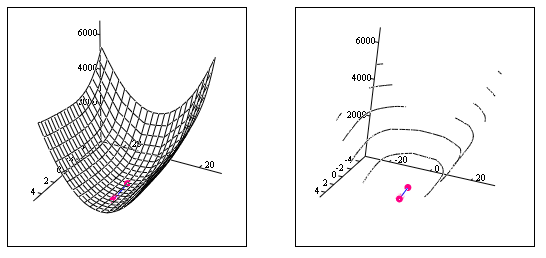
Минимизация функции

методом Дэвидона-Флетчера-Пауэлла

Контрольные вопросы и задания

1. Все алгоритмы главы выражены в виде задачи минимизации. Как простейшим способом использовать эти алгоритмы для максимизации, а не минимизации?

2. Пусть в точке градиент. Что можно сказать о точке, если

а) - выпуклая функция;

б) - вогнутая функция;

в) - неопределенная матрица;

г) - положительно определенная матрица;

д) - отрицательно полуопределенная матрица?

3. Является ли матрица Гессе для функции положительно определенной? Целесообразно ли использовать метод Ньютона для оптимизации этой функции?

4. Найдите направление, сопряженное к , для целевой функции.

5. Решите задачу минимизации функции , используя каждый из следующих методов:

а) метод Розенброка;

б) метод наискорейшего спуска;

в) метод Флетчера-Ривса;

г) метод Дэвидона-Флетчера-Пауэлла.

Сходятся ли методы? Если нет, то объясните почему.

Глава 4. Условная оптимизация

Ранее были рассмотрены методы решения задач безусловной оптимизации. Однако ряд инженерных задач связан с оптимизацией при наличии некоторого количества ограничений на независимые переменные. Эти ограничения существенно уменьшают размеры области, в которой проводится поиск оптимума и значительно усложняют решаемую задачу.

В этой главе рассматриваются необходимые условия существования экстремума нелинейной функции для задачи условной оптимизации (условия Куна-Таккера). Далее излагаются два основных подхода к решению таких задач, как штрафные функции и метод скользящего допуска.

Общая задача нелинейного программирования заключается в нахождении экстремума целевой функции при заданных ограничениях в виде равенств и (или) неравенств:

min,

при наличии ограничений

;

, .

Предполагается, что функции , известны, и хотя бы одна из них - нелинейная. Для задач нелинейного программирования разработаны алгоритмы нахождения локального минимума функции, причем различные алгоритмы применяются при решении задач с ограничениями только в виде равенств или с ограничениями только в виде неравенств.