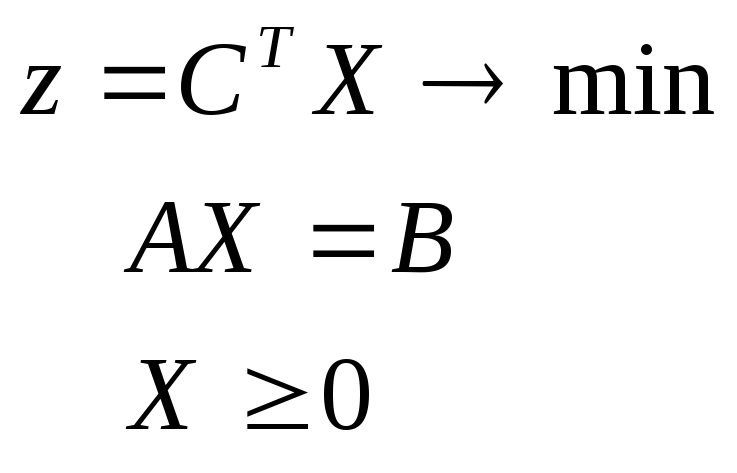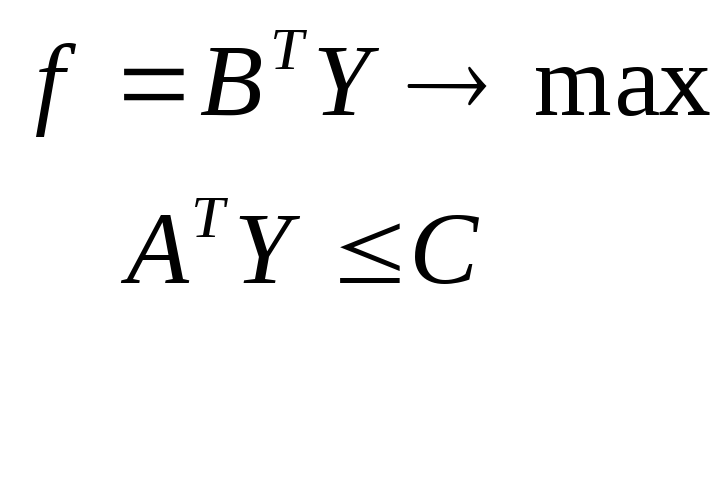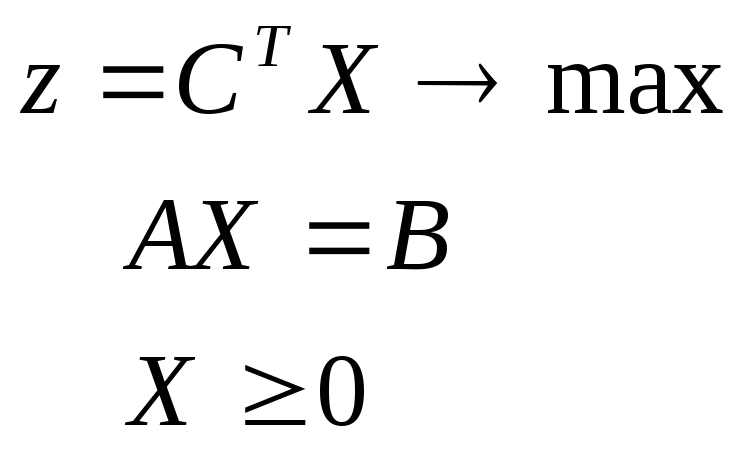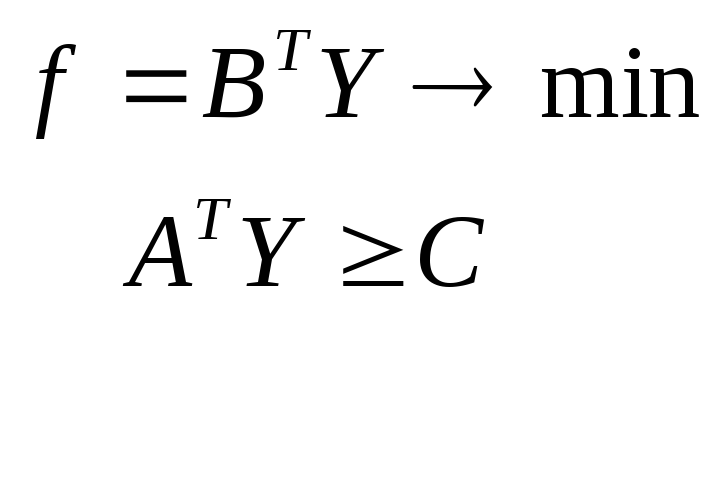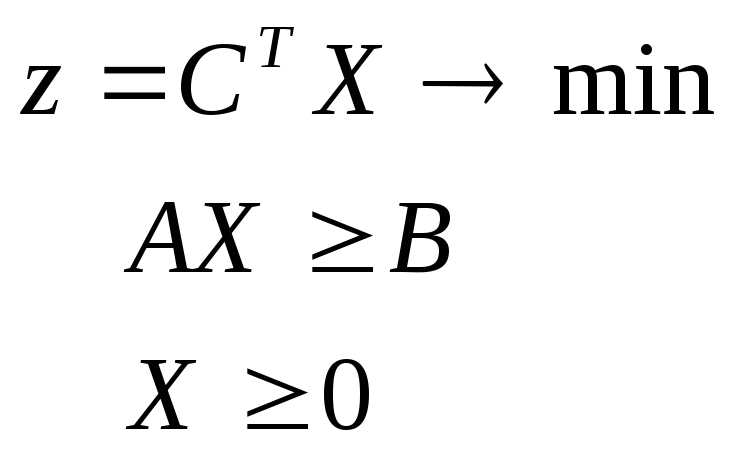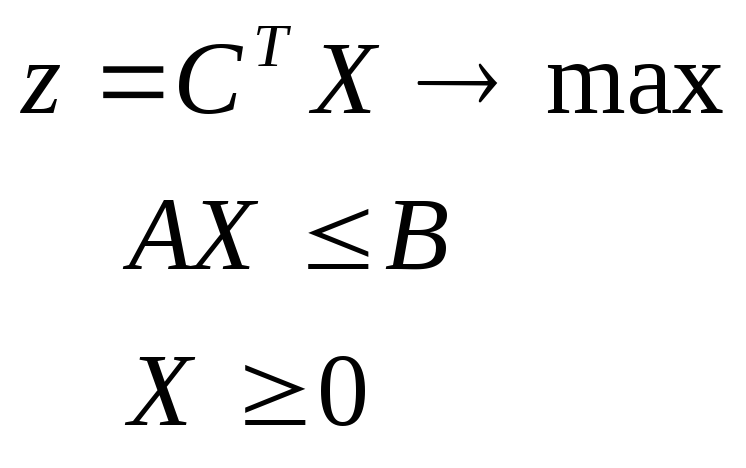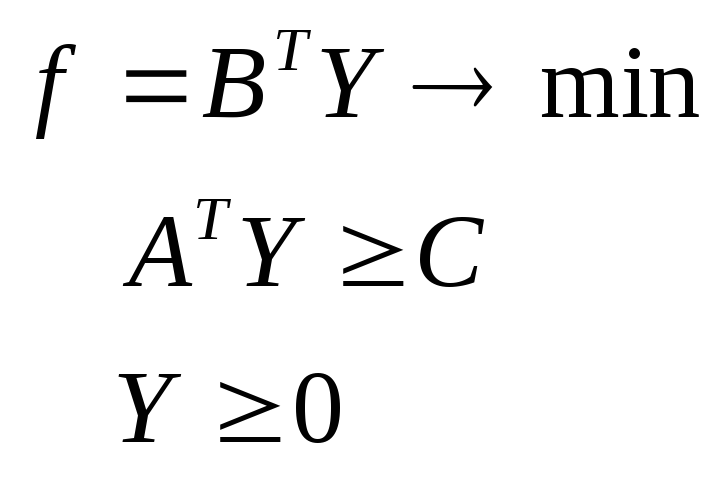4. Порождение начального допустимого базисного решения

При решении реальной задачи, представленной в виде математической модели ЛП, ограничения могут быть заданы в различных видах. Базисное допустимое решение не всегда очевидно. Необходимо указать метод автоматического порождения начального допустимого базисного решения.

Пусть в задачу ЛП входят ограничений и(исходных) переменных. Допустим среди всех ограничений задачиограничений имеют знак , ограничений имеют знак = и ограничений имеют знак , и эти ограничения расположены именно в таком порядке (). Предположим, что правые части ограничений положительны (все наши предположения не нарушают общности задачи).

Исходная задача имеет вид

при ограничениях

; ,

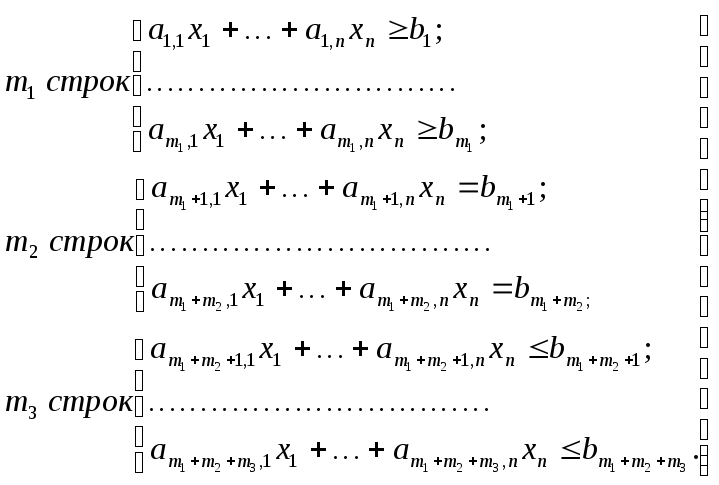
В первые ограничений введем дополнительные переменныес коэффициентом –1. В последниеограничений введем дополнительные переменныес коэффициентом +1. Далее в первыеограничений введем искусственные переменныес коэффициентом +1. Искусственные переменные вместе с последнимидополнительными переменными образуют начальное допустимое базисное решение, значения которых совпадают с правыми частями ограничений.

В целевую функцию дополнительные переменные входят с нулевыми коэффициентами, а искусственные - с коэффициентами, равными очень большому числу (машинной бесконечности). Это приводит к тому, что при минимизации искусственные переменные будут выводиться из базиса в первую очередь.

4. Двойственность в линейном программировании

Общая задача линейного программирования имеет вид

при ограничениях

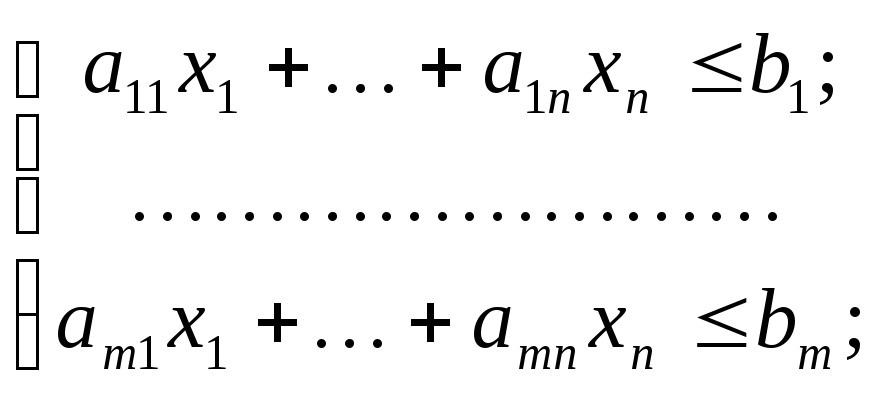(6)

; .

Задача, состоящая в нахождении минимума целевой функции

,

при наличии ограничений

(7)

называется двойственной по отношению к задаче (6).

Двойственная задача (7) составлена согласно следующим правилам:

• коэффициентами целевой функции двойственной задачи являются свободные члены системы ограничений исходной задачи;

• свободными членами системы ограничений двойственной задачи являются коэффициенты целевой функции исходной задачи;

• матрица коэффициентов системы ограничений транспонирована;

• если исходная задача поставлена на нахождение максимума, то двойственная задача ставится на определение минимума, и наоборот. Неравенства вида в системе ограничений исходной задачи заменяются неравенствами вида 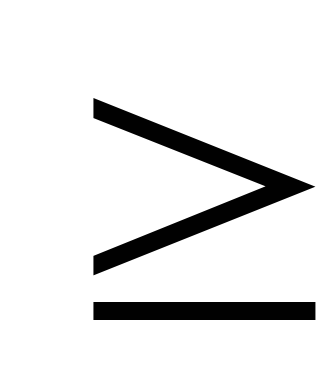в двойственной задаче, и наоборот.

Обычно говорят о паре двойственных задач линейного программирования. Всего существует четыре типа пар двойственных задач линейного программирования:

исходная задача двойственная задача

1. 

2. 

3. 

4. 

Первые две задачи называются несимметричными, а две последние - симметричными двойственными задачами линейного программирования. В несимметричных задачах двойственные переменные не имеют ограничения в знаке, что надо учитывать при решении симплекс-методом.

Связь между оптимальными решениями пары двойственных задач устанавливает теорема двойственности (для задач типа 3,4).

Теорема. Если из пары двойственных задач одна имеет конечное решение, то и другая будет иметь конечное решение, причем

.

Если целевая функция одной из задач не ограничена в области допустимых решений, то другая задача вообще не имеет решений (ее система ограничений несовместна).

Теория двойственности позволила усовершенствовать симплекс-метод и создать так называемый улучшенный симплекс-метод, который в основном и применяется. Улучшенный симплекс-метод позволяет получать сразу решение и исходной, и двойственной задач. Поэтому можно выбирать один из вариантов: решать ли задачу в том виде, в котором она поставлена, или решать двойственную задачу. Так как объем вычислений в задаче линейного программирования связан скорее с количеством ограничений, чем с количеством переменных, то можно порекомендовать переходить к двойственной задаче в случае, когда ограничений больше, чем переменных.

Теория двойственности позволяет также проводить анализ устойчивости решения при изменении коэффициентов , т.е. определяет границы изменения этих коэффициентов, при которых базис остается тем же самым, и решать всю задачу сначала нет необходимости. Кроме того, анализ изменений в виде введения дополнительного ограничения или исключения ограничения позволяет либо не решать задачу заново и воспользоваться уже существующим решением, либо существенно облегчить новое решение за счет уже существующего.

Все это имеет большое значение для практики, т.е. позволяет лицу, принимающему решение, ориентироваться при изменении условий: заранее знать изменится или нет оптимальное решение, нужен ли дополнительный анализ, понадобится ли еще раз принимать решение.