
- •Предисловие
- •1.1. Постановка и классификация задач
- •1.2. Основные определения
- •1.3. Классический метод определения экстремума функции
- •Контрольные вопросы и задания
- •Глава 2. Одномерная оптимизация
- •2.1. Интервал неопределенности
- •2.2. Метод дихотомии
- •2.3. Метод фибоначчи
- •2.4. Метод золотого сечения
- •2.5. Метод квадратичной интерполяции
- •Контрольные вопросы и задания
- •Глава 3. Оптимизация функций нескольких переменных
- •3.1. Методы прямого поиска
- •3.1.1. Метод покоординатного спуска
- •3.1.2. Метод поиска Хука – Дживса
- •Метод Розенброка (метод вращающихся координат)
- •Метод Нелдера-Мида (метод деформируемого многогранника)
- •Метод сопряженных направлений Пауэлла
- •3.1.6. Методы случайного поиска
- •3.2. Градиентные методы
- •3.2.1. Метод наискорейшего спуска
- •Метод сопряженных градиентов Флетчера и Ривса
- •3.3. Методы второго порядка
- •3.3.1. Метод Ньютона
- •3.3.2.Метод Дэвидона - Флетчера - Пауэлла
- •Итерационная процедура Дэвидона-Флетчер-Пауэлла может быть представлена последовательностью шагов.
- •Контрольные вопросы и задания
- •Глава 4. Условная оптимизация
- •4.1. Множители лагранжа
- •4.2. Условия куна - таккера
- •Методы решения задач условной оптимизации
- •4.3.1. Метод последовательной безусловной оптимизации
- •4.3.2.Метод скользящего допуска
- •Контрольные вопросы и задания
- •Глава 5. Линейное программирование
- •5.1. Постановка задачи лп
- •Тогда задача лп (1) - (3) запишется в виде
- •5..2. Каноническая и стандартная формы задачи лп
- •5.3. Симплекс - метод
- •Порождение начального допустимого базисного решения
- •Двойственность в линейном программировании
- •5.6. Транспортная задача
- •Контрольные вопросы и задания
- •Заключение
- •Библиографический список
- •Глава1. Безусловная оптимизация………..………4
- •Глава 2. Одномерная оптимизация………..….…….9
- •Глава 3. Оптимизация функций нескольких переменных………………………………………..….…..20
- •Глава 4. Условная оптимизация…………………..49
- •Глава 5. Линейное программирование…………..60
- •Лидия Ивановна Лыткина Методы оптимизации с программами в системе mathcad
- •660014, Красноярск, просп. Им. Газ. ”Красноярский рабочий”, 31.
3.1.2. Метод поиска Хука – Дживса
Процедура Хука и Дживса представляет собой комбинацию двух типов поиска: исследующий поиск и поиск по образцу. Исследующий поиск ориентирован на выявление характера локального поведения целевой функции и определение направлений вдоль “оврагов”.
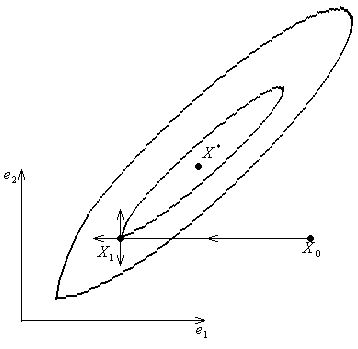
Рис. 6
Первые
![]() шаговисследующего
поиска
осуществляются аналогично первым
шаговисследующего
поиска
осуществляются аналогично первым
![]() шагам покоординатного спуска. Для
проведения исследующего поиска
необходимо задать величину шага, которая
может быть различной для разных
координатных направлений и изменяться
в процессе поиска. Исследующий поиск
начинается в некоторой исходной точке.
Если значение целевой функции в пробной
точке не превышает значения функции
в исходной точке, то шаг поиска
рассматривается как успешный. В противном
случае необходимо вернуться в предыдущую
точку и сделать шаг в противоположном
направлении с последующей проверкой
значения целевой функции. После перебора
всех
шагам покоординатного спуска. Для
проведения исследующего поиска
необходимо задать величину шага, которая
может быть различной для разных
координатных направлений и изменяться
в процессе поиска. Исследующий поиск
начинается в некоторой исходной точке.
Если значение целевой функции в пробной
точке не превышает значения функции
в исходной точке, то шаг поиска
рассматривается как успешный. В противном
случае необходимо вернуться в предыдущую
точку и сделать шаг в противоположном
направлении с последующей проверкой
значения целевой функции. После перебора
всех![]() координатных направлений исследующий
поиск завершается. Полученную в
результате точку называют базисной
точкой.
координатных направлений исследующий
поиск завершается. Полученную в
результате точку называют базисной
точкой.
Поиск по образцу заключается в реализации единственного шага из полученной базисной точки вдоль прямой, соединяющей эту точку с предыдущей базисной точкой. Новая точка образца определяется в соответствии с формулой
![]() .
.
Движение
по образцу считается успешным, если
исследующий поиск, проведенный из
точки
![]() ,
приводит к уменьшению целевой функции.
В этом случае полученная точка
рассматривается как новая базисная
точка
,
приводит к уменьшению целевой функции.
В этом случае полученная точка
рассматривается как новая базисная
точка![]() .
Если исследующий поиск, проведенный
после поиска по образцу, неудачен, то
необходимо вернуться в точку
.
Если исследующий поиск, проведенный
после поиска по образцу, неудачен, то
необходимо вернуться в точку![]() и провести исследующий поиск с целью
выявления нового направления минимизации.
В конечном счете возникает ситуация,
когда такой поиск не приводит к успеху.
В этом случае требуется уменьшить
величину шага при исследующем поиске
(например в 10 раз) и возобновить
исследующий поиск. Поиск завершается,
когда величина исследующего шага
становится достаточно малой.
и провести исследующий поиск с целью
выявления нового направления минимизации.
В конечном счете возникает ситуация,
когда такой поиск не приводит к успеху.
В этом случае требуется уменьшить
величину шага при исследующем поиске
(например в 10 раз) и возобновить
исследующий поиск. Поиск завершается,
когда величина исследующего шага
становится достаточно малой.
Метод Хука - Дживса характеризуется несложной стратегией поиска, относительной простотой вычислений и невысоким уровнем требований к объему памяти ЭВМ. Однако необходимо отметить, что в ряде случаев алгоритм может заканчивать работу преждевременно, а при наличии значительных нелинейных эффектов вырождается в последовательность исследующих поисков без перехода к ускоряющему поиску по образцу. В связи с чем разработан ряд методов, в которых устраняются эти недостатки.
Метод Розенброка (метод вращающихся координат)
Метод вращающихся координат избавлен от некоторых недостатков метода Хука и Дживса. Улучшение достигается построением новой системы ортогональных векторов, которая на каждой итерации выбирается с учетом структуры минимизируемой функции в окрестности полученной точки. Новая система координат направляет один из базисных векторов вдоль дна возможного оврага. Другие векторы новой системы - ортогональны. Схема построения новой системы координат проиллюстрирована на рис. 7.
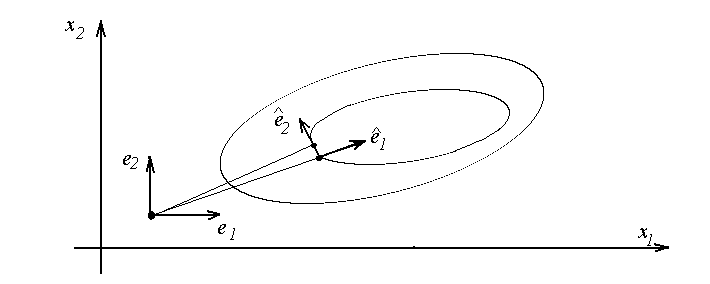
Рис. 7
Пусть
![]() - система единичных ортогональных
векторов. Тогда новая система векторов
- система единичных ортогональных
векторов. Тогда новая система векторов![]() строится с помощью процедуры Грама-Шмидта:
строится с помощью процедуры Грама-Шмидта:
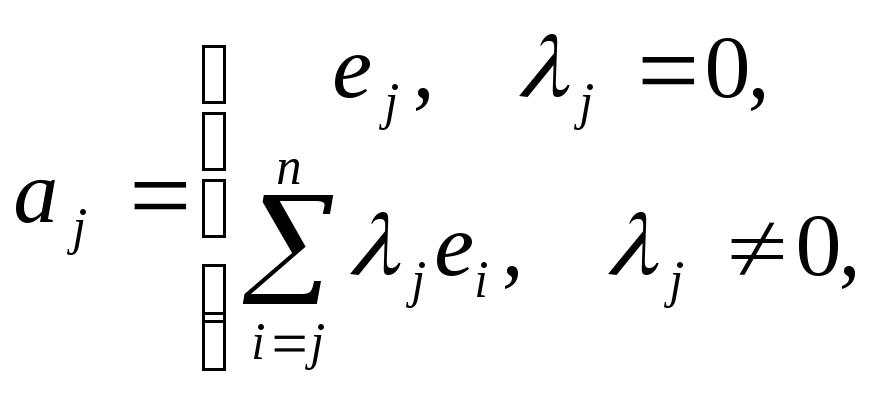
А
![]()
где![]() - скалярное произведение
- скалярное произведение![]() ,
,![]() - норма вектораbj
,
λj
- длина шага вдоль направления ej.
Можно показать, что система векторов
- норма вектораbj
,
λj
- длина шага вдоль направления ej.
Можно показать, что система векторов
![]() является
ортогональной.
является
ортогональной.
Алгоритм.
Начальный
этап.
Пусть
e1
,
e2
,
…,en
- координатные направления,![]() -начальное
приближение, ε>0 - малое число,
-начальное
приближение, ε>0 - малое число,
![]() ,
,
n = j = 1.
Основной этап:
a)
найти оптимальное решение λj
задачи минимизации
функции f(![]() +λej)
и положить
+λej)
и положить
![]() =
=![]() +
λjej;
если j < k,
то j=j+1, и вернуться к a); в противном
случае необходимо перейти к пункту b);
+
λjej;
если j < k,
то j=j+1, и вернуться к a); в противном
случае необходимо перейти к пункту b);
b)
пусть
![]() =
=
![]() ;
если
;
если
![]() ,
то вычисления прекращаются; в противном
случае необходимо положить
,
то вычисления прекращаются; в противном
случае необходимо положить
![]() =
=
![]() ,
принятьn
= n
+ 1, j
=1 и перейти к пункту c);
,
принятьn
= n
+ 1, j
=1 и перейти к пункту c);
с)
строим новую систему ортогональных
векторов
![]() и выполняем переход к пунктуa);
при этом векторы ej
принимаются равными векторам
и выполняем переход к пунктуa);
при этом векторы ej
принимаются равными векторам
![]()
Пример. Щелкнув по значку, откроется Mathcad документ метода Розенброка, в котором можно выполнить вычисления.

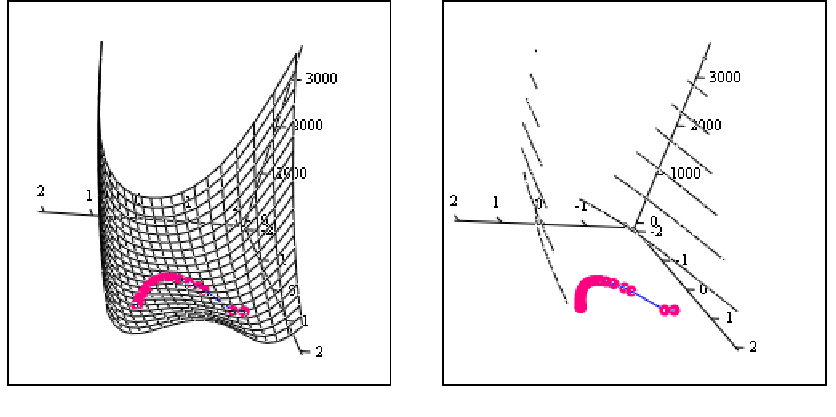
Минимизация
функции
![]()
методом Розенброка
