Тогда задача лп (1) - (3) запишется в виде

при ограничениях

Метод решения задачи (1) - (3) будет рассмотрен ниже.

5..2. Каноническая и стандартная формы задачи лп

Каноническая форма задачи ЛП имеет вид

при ограничениях

; ,

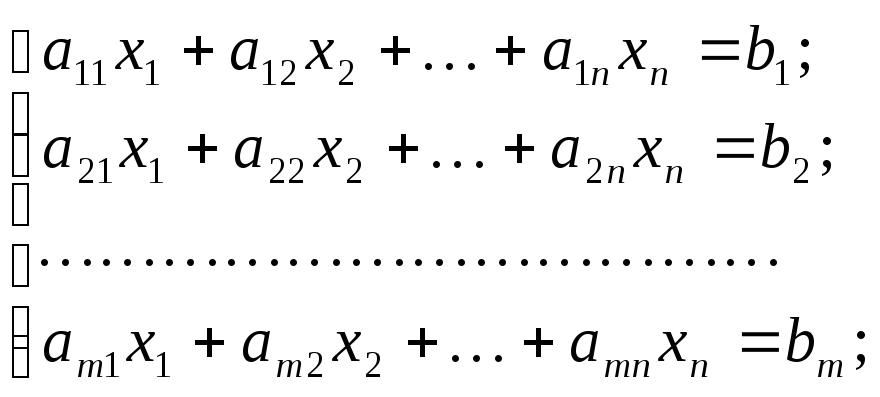
т.е. является задачей минимизации линейной функции с линейными ограничениями в виде равенств.

Запишем стандартные формы задачи ЛП:

при ограничениях

;

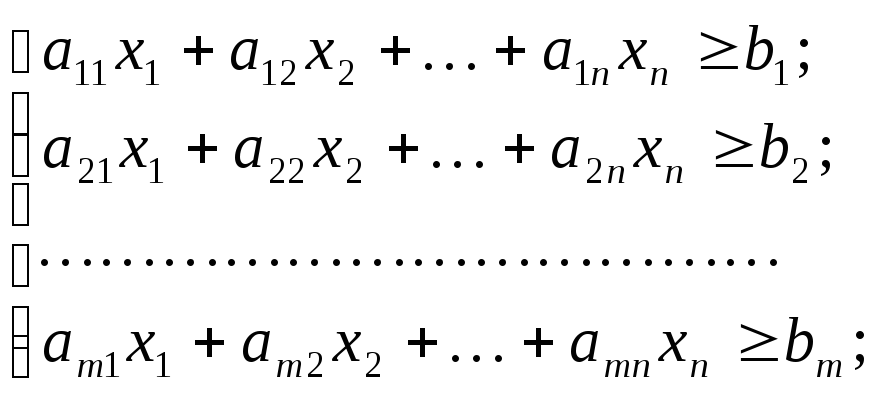
или

при ограничениях

; ,

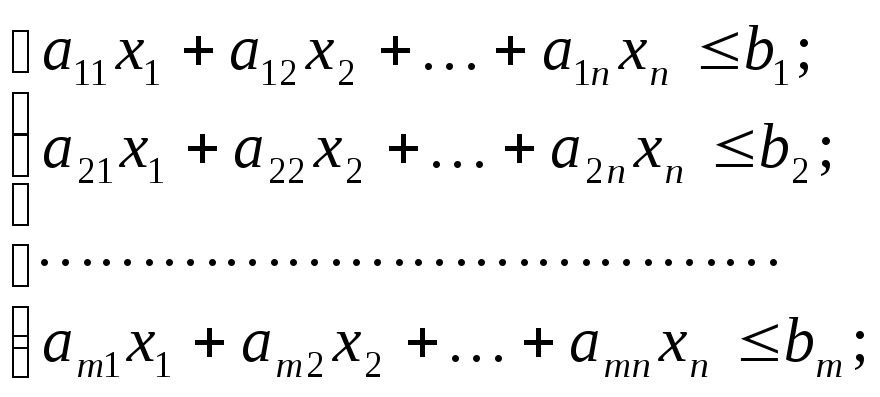
т.е. стандартная форма записи задачи ЛП требует, чтобы для задачи максимизации все ограничения были равенствами со знаком “меньше или равно”, а для задачи минимизации - со знаком “больше или равно”.

Указанные формы задачи ЛП эквивалентны в том смысле, что каждая из них может быть приведена к любой другой путем несложных преобразований. Это позволяет применять методы, разработанные для одной задачи ЛП, к любой другой. Чаще других используется каноническая форма.

Для того чтобы переходить от стандартной формы записи к канонической форме, нужно уметь преобразовать задачу максимизации к задаче минимизации и ограничения - неравенства к ограничениям - равенствам.

Задача максимизации функции может быть заменена задачей минимизации функции, поскольку.

Рассмотрим переход от неравенств к равенствам. Для того чтобы перейти от неравенств вида “” и “” к равенствам, требуется ввести дополнительные неотрицательные переменные, которые прибавляются к левым частям каждого неравенства вида “” и вычитаются из левых частей неравенств “”, обращая их в равенства, т.е. неравенство эквивалентно равенству, а неравенствоэквивалентно равенству.

В целевую функцию дополнительные переменные входят с нулевыми коэффициентами:

5.3. Симплекс - метод

Симплекс-метод, разработанный Данцигом в 1947 г. и опубликованный в 1949 г., является универсальной вычислительной процедурой для решения задач линейного программирования. Он непосредственно применяется к решению общей задачи ЛП в канонической форме:

при ограничениях

; ;

,

причем предполагается, что имеется базисное допустимое решение, удовлетворяющее всем ограничениям. Способ определения начального допустимого базисного решения укажем позже.

Предположим сначала, что система ограничений задачи сведена к следующему виду:

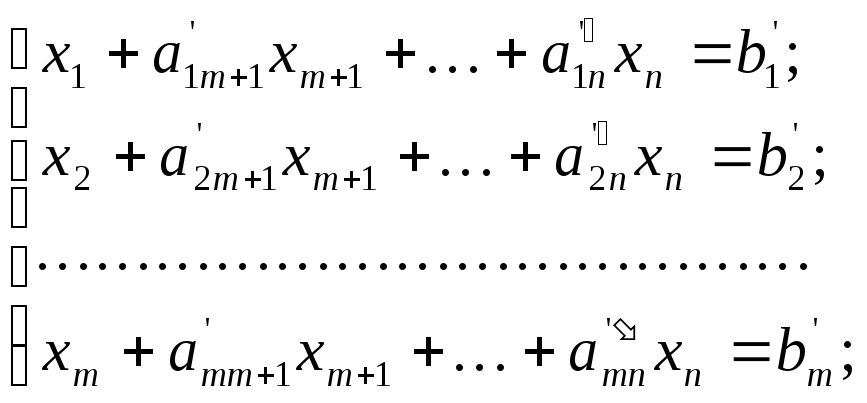(4)

; .

Система (4) может быть разрешена относительно переменных . Переменные, входящие с единичными коэффициентами только в одно уравнение системы и с нулевыми - в остальные, называются базисными. Остальныепеременных называются небазисными.

Базисным решением системы (4) называется решение, полученное при нулевых значениях небазисных переменных. Если умножить ограничения этой системы на и вычесть из целевой функцииz, то исключатся изz, и мы получим

, (5)

где

.

Получим ту же самую задачу , но в другой алгебраической форме (4),(5).

Если теперь задать равными нулю, то соотношения

задают базисное решение, а вектор является допустимым базисным решением, если все.

По определению - базисные переменные,- небазисные.

Среди такого вида допустимых базисных решений надо найти оптимальное, т.е. доставляющее минимум целевой функции. Симплекс-метод обеспечивает систематическую процедуру такой замены одного допустимого базисного решения на другое, при которой значение целевой функции уменьшается. Итерационный процесс симплекс-метода может быть описан следующим образом:

1. Найти переменную для включения в базис.

Переменные являются небазисными. Находим наименьший из коэффициентов. Пусть это будет коэффициент. Если, то увеличение, которое пока равно нулю, приведет к убыванию целевой функцииz. Очевидно, что если имеется несколько отрицательных , то разумно (но необязательно) выбрать наибольший по модулю.

Если же все , то значение функции не может быть уменьшено ни при каком выборе, а это означает, что минимум найден.

2. Найти переменную для исключения из базиса.

Пусть в -том ограничении . Покабыл равен нулю, это ограничение имело вид. Теперьи ограничение принимает вид. Так как, то наибольшее значение, которое может приниматьравно, иначедолжен стать отрицательным для выполнения ограничения.

Если , то при увеличениибудет возрастать и, т.е. нарушения условия неотрицательности не будет. Аналогичные рассуждения можно провести для всех. Это означает, чтоможет увеличиваться до значения

.

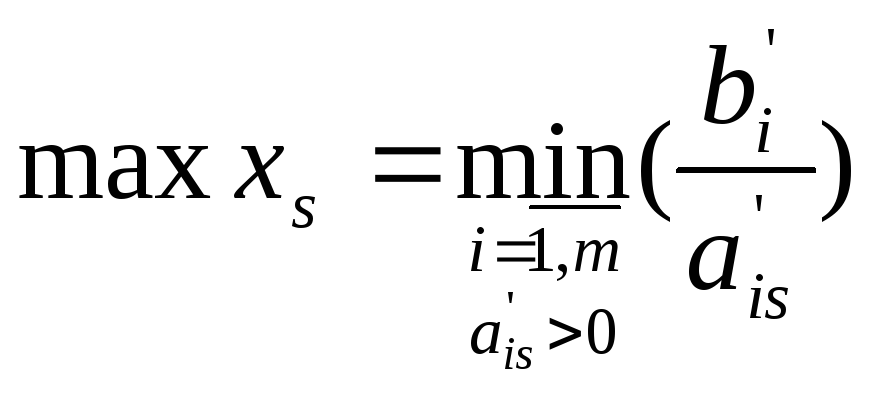Если этот минимум достигается в строке с номером r, то обращается в нуль, а. Другие базисные переменные останутся положительными (неотрицательными). Элементназывается ведущим элементом, строкаr - ведущей строкой, столбец s - ведущим столбцом.

3. Записать задачу в новой форме.

Переменная стала базисной и новый базис принимает вид. Чтобы новая форма записи нашей задачи была аналогичной предыдущей, надо сделать коэффициент прив ведущей строке равным единице, для чего нужно разделить эту строку на.

Затем необходимо исключить из других ограничений. Для этого к-той строке, имеющей коэффициентпри, прибавим ведущую строку (с коэффициентом 1 при), умноженную на -(,). Для преобразования целевой функции с отрицательным коэффициентомприприбавим к ней новую ведущую строку, умноженную на -.

Пример.Щелкнув по значку, откроется Mathcad документ графического метода решения задачи линейного программирования, в котором можно выполнить вычисления.

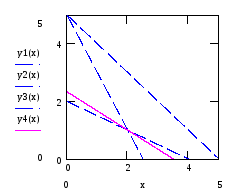
Графическое решение задачи ЛП для функции двух переменных

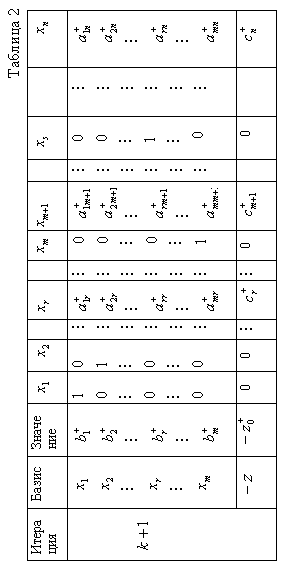
Итерационный процесс удобно проиллюстрировать в так называемых симплекс - таблицах.

Предположим, что начальная каноническая форма задана и что на -ой итерации получена каноническая форма, заданная уравнениями (1),(2), запись которых приведена в табл. 1

На очередной итерации каноническая форма будет записана в виде табл. 2.

Построив новую задачу (эквивалентную исходной) необходимо повторить последовательно все этапы симплекс-метода. В конце концов будет обнаружено, что все коэффициенты целевой функции неотрицательны, что и означает окончание процесса, т.е. задача решена. Она может иметь единственное конечное решение, неограниченное решение, бесконечное множество решений.

Если при этом некоторые коэффициенты целевой функции равны нулю, т.е. увеличение соответствующих переменных не будет изменять целевую функцию, то это означает, что имеется более, чем одно оптимальное решение.