3.2. Градиентные методы

Другая группа методов, разработанная для решения задач безусловной оптимизации, состоит из градиентных методов. Их еще называют методами первого порядка, или методами спуска. Эти методы используют как значения функции, так и значения частных производных первого порядка, поэтому могут быть применены для минимизации только дифференцируемых функций. Методы первого порядка сходятся быстрее методов прямого поиска, так как в них учитываются производные, характеризующие направление наиболее быстрого убывания функции. Рассмотрим некоторые из них.

3.2.1. Метод наискорейшего спуска

Такой метод является одной из наиболее фундаментальных процедур минимизации дифференцируемых функций нескольких переменных.

В методе наискорейшего спуска в качестве направления поиска выбирается вектор, направление которого противоположно направлению вектора градиента функции . Из математического анализа известно, что векторхарактеризует направление наиболее быстрого возрастания функции. Поэтому векторназывается антиградиентом и является направлением наиболее быстрого ее убывания. Рекуррентное соотношение, с помощью которого реализуется метод наискорейшего спуска, имеет вид

,

где - величина шага. В зависимости от выбора величины шага можно получить различные варианты градиентного метода. Если в процессе оптимизации величина шагафиксирована, то метод носит название градиентного метода с дискретным шагом. Процесс оптимизации на первых итерациях можно значительно ускорить, есливыбирать из условия

.

Для определения используется любой метод одномерной оптимизации. В этом случае метод называется методом наискорейшего спуска. Как правило, в общем случае недостаточно одного шага для достижения минимума функции, процесс повторяют до тех пор, пока последующие вычисления позволяют улучшать результат.

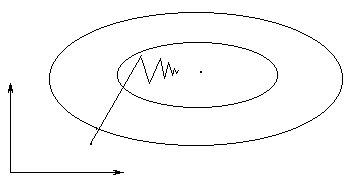
Рис. 14

Если пространство очень вытянуто по некоторым переменным, то образуется “овраг”. Поиск может замедлиться и идти зигзагами поперек дна “оврага” (рис. 14). Иногда решение невозможно получить за приемлемое время. Еще одним недостатком метода может быть критерий остановки , так как этому условию удовлетворяет и седловая точка, а не только оптимум.

Для ускорения сходимости градиентного метода в настоящее время разработано много различных приемов. Метод сопряженных градиентов один из них.

П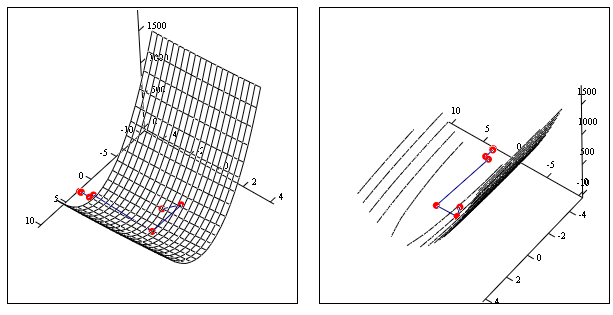ример.Щелкнув по значку, откроется Mathcad документ метода наискорейшего спуска, в котором можно выполнить вычисления.

Минимизация функции

методом наискорейшего спуска

2. Метод сопряженных градиентов Флетчера и Ривса

В этом методе направление спуска отклоняется от направления антиградиента за счет добавления к нему вектора направления, используемого на предыдущем шаге, умноженного на некоторое положительное число.

Направления поиска на каждой итерации определяются с помощью формулы.

,

где являются предыдущими направлениями поиска;- параметрами. Значения параметров выбираются таким образом, чтобы направлениебыло-сопряженным со всеми построенными ранее направлениями поиска. Доказано, что это условие будет выполняться при

,.

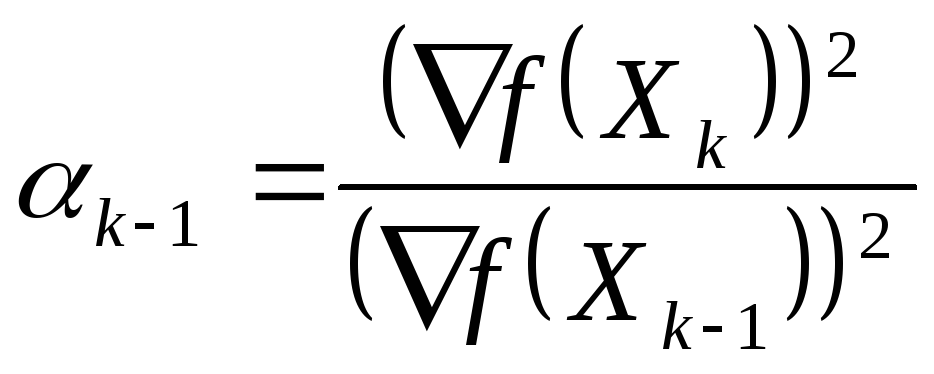Если минимизируемая функция квадратичная и выпуклая, то алгоритм сопряженных градиентов приводит к оптимальному решению не более чем за n выполненных линейных поисков. Практические исследования показали, что этот метод сходится быстрее метода наискорейшего спуска, причем его эффективность возрастает на завершающих этапах поиска минимума функции. Кроме этого, следует отметить, что данный метод может быть использован при минимизации функций с разрывными производными. Поиск “не зависает на изломе”, а идет вдоль линии, соединяющей точки изломов линий уровня, которая, как правило, проходит через точку минимума.

Алгоритм.

Начальный этап. Выбрать число  > 0 для остановки алгоритма и начальную точку . Положить = , = -f(), k = j = 1 и перейти к основному этапу.

Основной этап:

Шаг 1. Если ||f()|| < , то минимум найден. В противном случае взять в качестве _j оптимальное решение задачи минимизации функции f( + ) при   0 и положить =+_j. Если, то перейти к шагу 2; в противном слу­чае перейти

к шагу 3.

Шаг 2. Положить =-f()+_j, где _j=||f()||²/||f()||². За­менить j на j + 1 и перейти к шагу 1.

Шаг 3. Положить = = , = - f(), j=1, к = к+1 и перейти к шагу 1.

Пример. Щелкнув по значку, откроется Mathcad документ метода Флетчера-Ривса, в котором можно выполнить вычисления.

Минимизация функции

методом Флетчера – Ривса