2.5. Метод квадратичной интерполяции

Целевую функцию можно аппроксимировать полиномом второй степени на интервале . Предполагается, что на этом интервале функция унимодальна и выпукла. Тогда благоразумно в качестве минимума целевой функции принять минимум квадратичного полинома.

Если задана последовательность точек , такая что, и известны соответствующие этим точкам значения функции, то можно определить постоянные величинытаким образом, что значения квадратичной функции

совпадут со значениями в трех указанных точках. Коэффициентыможно определить из следующей системы линейных уравнений:

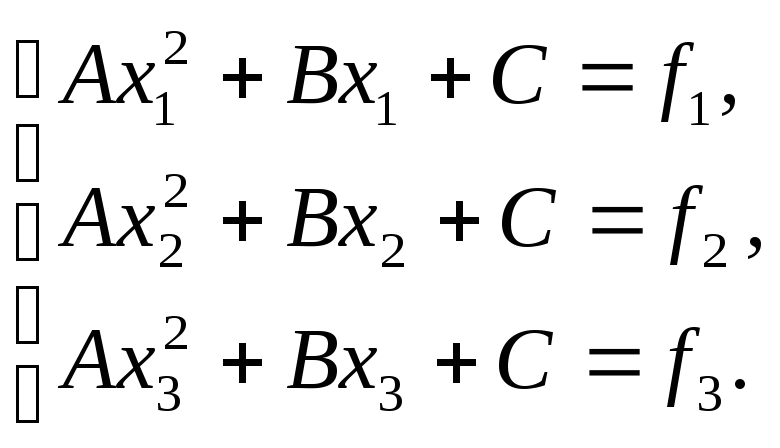
Так как полином имеет минимум в точке, еслиА>0, то точка минимума функцииможет быть аппроксимирована значением

.

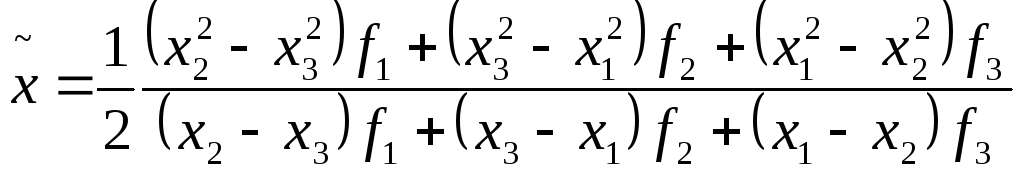Алгоритм.

Шаг 1. Выбрать три точки такие чтои.

Шаг 2. Вычислить точку , используя формулу определения точки минимума квадратичного полинома.

Шаг 3. Проверить условие окончания поиска. Если и, то закончить поиск. В противном случае повторить шаг 4.

Шаг 4. Выбрать наилучшую точку илии две точки по обе стороны от нее. Перейти к шагу 2.

Этот метод имеет недостатки. Если плохо аппроксимирует целевую функциюв выбранной окрестности, то минимум функциибудет плохой оценкой для решения задачи. На практике точкаможет оказаться вне начального интервала неопределенности.

Метод квадратичной интерполяции сходится сверхлинейно.

Таким образом, методы исключения интервалов основаны на процедуре простого сравнения значений функции в двух пробных точках. Метод точечного оценивания позволяет определить точку оптимума с помощью полиномиальной аппроксимации. В условиях, когда интервалы сходимости сравнимы между собой, а исследуемая функция является достаточно гладкой и унимодальной, метод точечного оценивания сходится значительно быстрее, чем методы исключения интервалов. Однако при исследовании быстро изменяющихся функций наиболее надежными являются методы золотого сечения и Фибоначчи.

Пример. Щелкнув по значку, откроется Mathcad - документ метода квадратичной интерполяции, в котором можно выполнить вычисления.

Минимизация функции

методом квадратичной интерполяции

Контрольные вопросы и задания

1. По какому принципу происходит сокращение интервала неопределенности при минимизации функции методом дихотомии?

2. Каким образом выбираются внутренние точки при минимизации функции методом Фибоначчи?

3. Какие из методов оптимизации функций одной переменной являются в целом более эффективными?

4. Определите точки золотого сечения на интервале (-1; 5).

5. Сформулируйте критерий остановки работы метода Фибоначчи.

6. Во сколько раз сократится начальный интервал при использовании метода Фибоначчи, если функция может быть вычислена только в семи точках?

7. Пользуясь любым из методов одномерного поиска, минимизируйте следующие функции с точностью до одного знака после запятой:

7.1. в интервале (0;4);

7.2. в интервале.

Глава 3. Оптимизация функций нескольких переменных

Здесь рассмотрим минимизацию функций нескольких переменных. Несмотря на то, что большинство практических задач содержит ограничения, изучение методов безусловной оптимизации важно. Многие алгоритмы решения задачи с ограничениями предполагают сведение ее к последовательности задач безусловной оптимизации.

К методам прямого поиска относятся покоординатный спуск, методы Хука-Дживса, Розенброка, Нелдера-Мида, метод сопряженных направлений и методы случайного поиска.

Градиентные методы (наискорейший спуск, метод Флетчера-Ривса) и методы второго порядка (Ньютона, Дэвидона-Флетчера-Пауэлла) в процессе поиска используют больше информации о целевой функции, чем методы прямого поиска и являются более эффективными.