
Vychislitelny_praktikum
.pdf
τk(2,и) = |
|
0,4 |
, |
(5.33) |
|
||||
где τ0 = |
|
τ0 |
|
|
τ – интервал дискретизации случайного процесса. |
|
|||
Подставив выражение (5.33) в (5.31), получим |
|
|||
ωэ,k |
= 0,2π . |
(5.34) |
||
|
|
τ0 |
|
|
Отсюда можно определить численное значение параметра масштаба для любого ортогонального базиса при m членов разложения ряда (5.16).
В таблице 5.10 приведены основные соотношения для определения α /γ для различных ортогональных базисов.
|
Определения параметра масштаба ортогональных функций |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Лагерра, Лежандра, Дирихле |
|
|
Таблица 5.10 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ψk (τ ,γ / α) |
|
|
|
|
|
Wm (jω) |
|
2 |
|
|
|
|
|
ωэ,m |
|
|
τm(2,)и |
|
|
|
α |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Lk (τ ,α) |
|
|
|
|
|
|
α 2 |
|
|
|
|
|
|
|
|
πα |
|
2 |
|
|
|
|
0,8 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
τ0 |
||||
|
|
|
ω2 +α 2 / 4 |
|
|
|
|
|
α |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Legk (τ,α) |
|
|
|
4(2m +1)2 α 2 |
|
π(2m + 1)α |
|
1 |
|
|
|
|
0,4 |
|
|
|
|||||||||||||||||
|
|
(2m +1)2 α 2 |
|
+ω2 |
|
|
2 |
|
|
(2m + 1)α |
|
|
(2m +1) τ0 |
|
|||||||||||||||||||
|
|
|
|
4(m |
+ |
1) |
2 |
α |
2 |
|
|
|
π |
(m |
+ |
α |
1 |
|
|
|
0,4 |
|
|
|
|||||||||
Dk (τ ,α) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(m + 1)α |
|
|
(m +1) τ0 |
|||||||||
|
|
|
(m +1)2 α 2 |
|
+ω2 |
|
|
2 |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
В таблице 5.11 приведены основные соотношения для определения параметра масштаба γ для ортогональных функций Якоби (α,0) и Сонина-Лагерра.
Определения параметра масштаба ортогональных функций Якоби (α,0) и Сонина-Лагерра
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 5.11 |
|||
ψ |
k |
(τ ,γ / α) |
|
|
|
|
|
W (jω) |
|
2 |
|
|
|
|
ωэ,m |
|
|
τ (2) |
|
|
γ |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m,и |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
P(−1 2,0)(τ,γ) |
|
|
|
|
γ 2 (4m +1)2 |
|
|
|
π |
(4m |
+ |
γ |
2 |
|
|
0,8 |
|
|
||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
4m +1 |
|
|
|
|
|
|
|
|
|
|
|
1) |
|
|
|
|
|
|
|
|
|
|
||||||||
|
k |
|
|
|
γ |
2 |
+ω |
2 |
|
|
4 |
|
|
(4m + 1)γ |
|
(4m +1) τ0 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
γ 2 (4m + 3)2 |
|
|
|
π |
|
+ |
γ |
2 |
|
|
0,8 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Pk(1 2,0)(τ,γ) |
|
|
4m + 3 |
|
2 |
|
|
|
|
|
|
|
(4m |
|
3) |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
γ |
2 |
+ω |
2 |
|
|
4 |
|
|
(4m + 3)γ |
|
(4m + 3) τ0 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
P( 1,0 ) (τ,γ) |
|
|
|
|
4γ 2 (m +1)2 |
|
|
|
π(m +1)γ |
|
1 |
|
|
|
0,4 |
|
|
|||||||||||||||
|
|
|
|
(m +1)2 γ 2 +ω2 |
|
|
|
|
2 |
|
|
|
(m +1)γ |
|
|
(m +1) τ0 |
||||||||||||||||
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
P( 0,0 ) (τ,γ) |
|
|
|
|
4γ 2 (2m +1)2 |
|
|
|
π(2m + 1)γ |
|
1 |
|
|
|
0,4 |
|
|
|||||||||||||||
|
|
(2m +1)2 γ 2 +ω2 |
|
2 |
|
|
(2m + 1)γ |
|
(2m +1) τ0 |
|||||||||||||||||||||||
|
k |
|
|
|
|
|
|
|||||||||||||||||||||||||
63

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
4γ 2 (2m + 3)2 |
π |
|
+ |
γ |
|
1 |
|
|
0,4 |
|
|
|
||||||||
P( 2,0 ) (τ,γ) |
|
|
|
|
|
|
|
|
(2m |
|
3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2m + 3)2 γ 2 +ω2 |
|
2 |
|
|
(2m + 3)γ |
|
|
(2m + 3) τ0 |
|
|||||||||||||
k |
|
|
|
|
|
|
|
|
|
|||||||||||||||
L(k1)(τ ,γ ) |
|
|
|
γ 4 (m +1)2 |
|
|
πγ |
|
|
|
4 |
|
|
|
1,6 |
|
|
|
||||||
|
|
|
(γ 2 / 4 +ω2 )2 |
|
|
|
8 |
|
|
|
γ |
|
|
|
|
τ0 |
|
|||||||
(2 ) |
|
|
γ 6 (m + 1)2 (m + 2)2 |
|
πγ |
|
|
16 |
|
6 ,4 |
|
|
|
|||||||||||
(τ ,γ ) |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Lk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
4(γ 2 / 4 + ω2 )3 |
|
|
32 |
|
|
3γ |
|
|
|
3 τ0 |
|
|
||||||||||
В таблице 5.12 приведены основные соотношения для определения параметра масштаба γ для ортогональных функций Якоби (0,β ).
Определения параметра масштаба ортогональных функций Якоби (0,β )
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 5.12 |
|
|
|
|
|
Wm (jω) |
|
|
|
2 |
|
|
|
|
|
|
|
64(m + 1)6 γ 4 |
|||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
[(2m + 1)2 γ 2 + ω2 ][(2m + 3)2 γ 2 + ω2 ] |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
πγ(2m + 1)(2m + 3) |
|||||||
Pk |
( , |
) |
|
|
|
ωэ,m |
|
|
|
|||||||||||||||
( 0,1) τ γ |
|
|
|
|
|
|
|
|
|
|
|
|
8(m + 1) |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4(m + 1) |
|||||
|
|
|
|
|
|
τ (2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
m ,и |
|
|
|
|
|
|
|
|
γ (2m + 1)(2m + 3) |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,6(m + 1) |
|
||||
|
|
|
|
|
|
γ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2m + 1)(2m + 3) τ0 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 (2m + 3)2 (m + 1)4 (m + 2)4 γ 6 |
||||||||||
|
|
|
|
|
Wm (jω) |
|
|
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
[(2m + 1)2 γ 2 + ω2 ][(2m + 3)2 γ 2 + ω2 ][(2m + 5)2 γ 2 + ω2 ] |
|||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3πγ(2m + 1)(2m + 3)(2m + 5) |
|||||||||
|
|
|
|
|
|
ωэ,m |
|
|
|
|||||||||||||||
( 0,2 ) τ γ |
) |
|
|
|
|
|
|
|
|
|
|
|
64(m + 1)(m + 2) |
|||||||||||
Pk |
( , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32(m + 1)(m + 2) |
||||||
|
|
|
|
|
|
τ (2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
m ,и |
|
|
|
|
|
3γ (2m + 1)(2m + 3)(2m + 5) |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12,8(m + 1)(m + 2) |
|
|||||
|
|
|
|
|
|
γ |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 τ0 (2m + 1)(2m + 3)(2m + 5) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Так как для колебательных моделей КФ с погрешностью восстановления 2% |
|||||||||||||||||||||||
|
|
τ0 |
= |
0,4 |
|
|
|
|
, |
(5.35) |
||||||||||||||
|
|
λ2 |
+ω2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
выражения для определения параметра масштаба для различных ортогональных функций примут вид, представленный в таблице 5.13.
64

Параметр масштаба для колебательных моделей
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 5.13 |
ψk (τ ,γ / α) |
|
|
|
|
|
α / γ |
|
||||||||
Lk (τ ,α) |
|
|
|
2 λ2 +ω02 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
L(k1)(τ ,γ ) |
|
|
|
4 λ2 + ω02 |
|
||||||||||
(2 ) |
(τ ,γ ) |
|
|
16 λ2 + ω02 |
|
||||||||||
Lk |
|
|
|
|
|
3 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Legk (τ,α) |
|
|
|
|
|
λ2 + ω02 |
|
||||||||
Pk( 0,0 ) (τ,γ) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
(2m + 1) |
|
|||||||||
Dk (τ ,α) |
|
|
|
|
|
λ2 +ω2 |
|
||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(m + 1) |
|
|
|
|
|
|
P(−1 2,0)(τ,γ) |
2 |
λ2 +ω02 |
|
||||||||||||
k |
|
|
|
|
|
|
|
|
(4m +1) |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(1 2,0) |
(τ,γ) |
2 |
λ2 +ω02 |
|
|||||||||||
Pk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4m + 3) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||
( 1,0 ) |
(τ,γ) |
|
|
|
|
|
λ2 +ω02 |
|
|||||||
Pk |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
(m +1) |
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||
( 2,0 ) |
(τ,γ) |
|
|
|
|
|
λ2 +ω02 |
|
|||||||
Pk |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
(2m + 3) |
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||
( 0,1) |
(τ,γ) |
|
|
4(m + 1) λ2 + ω02 |
|
||||||||||
Pk |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
(2m + 1)(2m + 3) |
|
|||||||||||
|
|
|
|
|
|
|
|||||||||
( 0,2 ) |
(τ,γ) |
|
32(m + 1)(m + 2) λ2 + ω02 |
|
|||||||||||
Pk |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
3(2m + 1)(2m + 3)(2m + 5) |
|
||||||||||||
|
|
|
|
|
|
||||||||||
В работе [22] показано, что для ортогональных функций Лагерра параметр
масштаба α может быть определен в результате решения уравнения |
|
|||
|
β0 = 1. |
|
|
(5.36) |
Рассмотрим это же уравнение для ортогональных функций, |
у которых |
|||
μ(τ )= 1 , в общем виде |
|
|||
1 |
|
∞∫ρx (τ )ψk* (τ ,α)dτ −1 = 0 , |
(5.37) |
|
|
ψk (α) |
2 |
||
|
|
0 |
|
|
где ψk* (τ ,α)= exp(−τ / 2 ψk (α)
 2 ).
2 ).
65

|
Как видно из выражения (5.37), численное значение параметра масштаба зави- |
|||||||||||||||||||||||||||||||||||||||||||||
сит от вида корреляционной функции. Так для |
ρ |
x5 |
(τ )= e−λ |
|
τ |
|
cosω τ |
это уравнение |
||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||
приведем к виду: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
||||||||||||||
cosω τ exp[− (1 / 2 ψ (α) 2 |
+ λ)τ ]dτ −1 = 0 . |
|
|
|
(5.38) |
|||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
∞ |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ψk (α) |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
2 ∫ |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ψk (α) |
|
|
|
2 , получим: |
|
|
|
|
|||||||||
|
|
Разрешив уравнение относительно 1 / |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
1 / ψk (α) 2 |
|
= 2 |
λ2 +ω02 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.39) |
|||||||||||||||
|
Результаты определения параметра масштаба для различных ортогональных |
|||||||||||||||||||||||||||||||||||||||||||||
функций представлены в таблице 5.14. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Параметры масштаба ортогональных функций для 5 модели |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 5.14 |
№ |
|
|
|
|
|
|
|
|
|
|
|
|
|
{ψk (τ ,α / γ )} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α0 (γ0 ) |
|
||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Lk (τ ,α) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 λ2 +ω02 |
|
||||||||||||
2 |
|
|
|
|
|
|
|
|
D |
|
(τ ,α ), P (1,0 )(τ ,γ ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
λ2 +ω |
|
2 |
/ (k +1) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
P (−1 / 2,0 ) |
(τ ,γ ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 λ2 +ω |
2 |
/ (4k +1) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
4 |
|
|
|
|
|
|
|
|
Leg |
k |
(τ ,α ), P (0 ,0 )(τ ,γ ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
λ2 +ω2 |
|
/ (2k +1) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
P (1 / 2,0 )(τ ,γ ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 λ2 +ω |
2 |
/( 4k + 3 ) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||||||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
P (2,0 )(τ ,γ ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ2 +ω2 |
|
/( 2k + 3 ) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||||
|
Решив |
|
|
|
|
уравнение |
(5.37) |
|
|
|
|
|
для |
|
|
|
|
|
|
корреляционных |
функций |
|||||||||||||||||||||||||
ρx,6 ,7 (τ )= e |
−λ |
|
τ |
|
|
|
|
|
|
|
λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
sinω0 |
τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
cosω0τ ± |
|
|
|
|
, получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
= 2 ( |
|
|
ω0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 / ψk (α) 2 |
|
|
2λ2 +ω02 |
mλ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.40) |
||||||||||||||||||||
|
Результаты определения параметра масштаба для различных ортогональных |
|||||||||||||||||||||||||||||||||||||||||||||
функций представлены в таблице 5.15. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
Параметры масштаба ортогональных функций для 6,7 моделей |
Таблица 5.15 |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ |
|
|
|
|
|
|
|
|
|
|
|
|
|
{ψk (τ ,α / γ )} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α (γ ) |
|
||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Lk (τ ,α) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 ( 2λ2 +ω02 mλ) |
||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Pk (−1 / 2 ,0 )(τ ,γ ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 ( 2λ2 + ω02 m λ)/ (4m + 1) |
||||||||||||||||
3 |
|
|
|
|
|
|
|
|
Dk (τ ,α ), Pk (1,0 )(τ ,γ ) |
|
|
|
|
|
|
|
|
|
|
|
|
( |
2λ2 |
+ω02 |
|
m λ)/ (m + 1) |
||||||||||||||||||||
4 |
|
|
|
|
|
|
|
Legk (τ ,α ), |
Pk (0 ,0 )(τ ,γ ) |
|
|
|
|
|
|
|
|
|
|
|
|
( |
2λ2 |
+ ω02 m λ)/ (2m + 1) |
||||||||||||||||||||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Pk (1 / 2 ,0 )(τ ,γ ) |
|
|
|
|
|
|
|
|
|
|
|
|
2 ( 2λ2 + ω02 m λ)/( 4m + 3 ) |
|||||||||||||||||||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Pk (2 ,0 )(τ ,γ ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 2λ2 +ω02 m λ)/( 2m + 3 ) |
||||||||||||||||
66

Для ортогональных функций Сонина-Лагерра одно из возможных решений, обеспечивающее допустимую погрешность аппроксимации и лучшую сходимость с наименьшими вычислительными затратами, связано с введением ограничения (5.36) [21].
Решим уравнение
1 |
|
|
|
|
|
∞ (α ) |
|
|
|
|
|
|
−λτ |
|
|
|
|
|
|
|
|
|
λ |
|
|
|
|
|
|
|
|
|
α |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫L0 (τ |
,γ )e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
(α ) |
|
|
|
2 |
|
|
|
cosω0τ |
± |
ω0 |
|
sinω0τ |
|
τ dτ = 1 |
(5.41) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
L |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
для моделей ρx ,6 ,7 (τ )= e |
−λ |
|
τ |
|
|
|
|
|
|
|
|
|
λ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
± |
|
|
|
|
sinω0 |
τ |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
cosω0τ |
ω0 |
|
. |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Проведя ряд преобразований, выражение (5.41) представим в виде: |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
α! |
|
|
|
|
λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
K1 ± |
K 2 = 1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.42) |
|||||||||||||||||||||||||
|
2 |
|
L(α ) |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
ω0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где K1 = |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
1 |
|
|
|
|
|
|
; |
|
|
|
|
|||||||||||
γ |
+ λ + |
jω |
|
|
α +1 |
|
|
γ |
+ |
λ − |
|
jω |
|
|
α +1 |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
2 |
|
0 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
K 2 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|||||||||||||
γ |
+ λ + |
jω |
|
|
α +1 |
|
|
|
γ |
+ |
λ − |
jω |
|
α +1 |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
2 |
0 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Введем некоторые упрощения, позволяющие представить уравнение (5.42) в форме, удобной для дальнейшего преобразования и применения:
1.с увеличением параметра α K 2 принимает ничтожно малые значения, которыми можно пренебречь;
2.наиболее простой вид уравнение принимает при значении α = 0 .
Тогда с учетом принятых упрощений получим уравнение
|
|
|
γ |
+ λ |
|
|
|
|
γ |
|
|
|
|
|
|||
|
|
2 |
|
|
|
= 1 . |
(5.43) |
|
|
|
|
2 |
|
||||
2 |
|
γ |
|
2 |
|
|
|
|
|
|
|
+ λ |
+ω0 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
Проведя ряд преобразований, и решив получившееся квадратное уравнение с учетом того, что параметр масштаба γ > 0 , получим
γ = 2 λ2 +ω02 . |
(5.44) |
Следует отметить, параметр масштаба γ , определенный по алгоритму (5.36), находится вблизи оптимального значения γopt , и обеспечивает погрешности аппрок-
симации, близкие к минимальным погрешностям. На рис. 5.4 построены двумерные зависимости относительной погрешности аппроксимации при разных значениях m и рассматриваемых α от параметра масштаба, где в качестве модели КФ взята модель
ρx ,6 (τ )= e |
−λ |
|
τ |
|
|
λ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
sinω0 |
τ |
|
|
с параметрами λ = 1 и ω0 |
= 5 . |
|
|
|
|
|
|
||||||||
|
|
|
|
cosω0τ + |
ω0 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
67

На рис. 5.5 представлены проекции двумерных зависимостей (см. рис. 5.4), представляющий относительную погрешность аппроксимации на плоскость m = 5 при заданных значениях α в одной системе координат. Заметим, что прямая линия на рисунке символизирует найденное решение (5.44).
Рисунок 5.4 - Двумерные зависимости относительной погрешности аппроксимации от параметра масштаба γ (0,40] и числа членов m [2,6] для α = 0, 1, 2
Рисунок 5.5. - Зависимости относительной погрешности аппроксимации от параметра масштаба γ (0, 60] при m = 5 для α = 0,1, 2
Из рис. 5.5 видно, что значение γ , полученное в результате решения уравнения
(5.41), при всех исследуемых значениях параметра α располагается вблизи глобального оптимума, и с увеличением данного параметра решение (5.44) становится более близким, что объясняется правильностью введенных выше упрощений.
Аналогичные результаты можно получить и для ортогональных функций Якоби (0,β ), Чебышева 1 (аналогично Якоби (− 0,5 ,0)), Чебышева 2 (аналогично Якоби
(0,5 ,0)), выполнив преобразования (5.41) - (5.44) [47].
Ниже для примера на рис. 5.6 приведены результаты аппроксимации КФ 5 модели при произвольном выборе численного значе-
ния α =7,000 , m = 12
(левая ветвь).
Рисунок 5.6 - Аппроксимация КФ ортогональными Полученные ре- функциями Лагерра
68

зультаты можно обобщить на аппроксимацию взаимных корреляционных функций ортогональными функциями. При этом необходимо аппроксимировать как правую, так и левую ветви взаимной корреляционной функции, т. е. необходимо искать модель в виде:
|
|
|
|
m1 |
|
|
|
|
m 2 |
|
|
|
|
|
Kaxy |
(τ )= |
Amax ∑βk ,п 1(τ )ψk |
(τ ,α1 )+ ∑βk ,л |
1(−τ )ψk |
(−τ ,α2 |
) |
, |
(5.45) |
||||||
где |
|
|
|
k =0 |
|
|
|
|
k |
|
|
|
|
|
1, |
τ > 0; |
0, |
|
τ > 0; |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
1(τ )= |
1 |
|
, τ = 0; и 1(−τ ) |
= |
1 |
|
, |
τ = 0; |
|
|
|
|
(5.46) |
|
|
|
|
|
|
|
|||||||||
|
2 |
τ < 0 |
2 |
|
τ < 0, |
|
|
|
|
|
||||
|
0, |
1, |
|
|
|
|
|
|
||||||
Amax |
|
|
|
|
|
|
|
|
|
|
||||
=σxσ y - наибольшее значение ВКФ; |
|
|
|
|
|
|||||||||
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
βk ,п |
= αп ∫ρxy (τ )ψn (τ ,αп )dτ ; |
|
|
|
|
|
|
|
|
|
(5.47) |
|||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||
βk ,л |
=αл∞∫ρyx (τ )ψn (τ ,αл )dτ . |
|
|
|
|
|
|
|
|
|
(5.48) |
|||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||
Исследования показали, что это будет справедливо, если максимум взаимной корреляционной функции будет находиться в «нуле». В противном случае в нулевой точке будет наблюдаться выброс (см. рис. 5.7).
Рисунок 5.7 - Результаты аппроксимации корреляционной функции ортогональными функциями Лагерра
Из анализа результатов видно, что даже при аппроксимации простейших моделей взаимных корреляционных функций ортогональными функциями, например Лагерра, для обеспечения допустимых погрешностей необходимо определять большое
69

число членов разложения ряда (в рассматриваемом примере m = 40 ). Кроме того, после аппроксимации необходима нормировка, так как значение модели корреляционной функции в нуле не равно 1. Эти обстоятельства без модификации модели затрудняют её применение.
Для устранения этих недостатков необходимо, в первую очередь, определить τm - значение аргумента, при котором Kaxy (τ ) достигает своего максимального зна-
чения, и искать модель взаимной корреляционной функции в виде:
|
m1 |
m2 |
|
|
, |
(5.46) |
Kaxy(τ)= Amax ∑βk,п 1(τ −τm )ψk |
(τ −τm ,α1 )+∑βk,л 1(τm −τ)ψk (τm −τ,α2 ) |
|||||
|
|
k |
|
|
|
|
|
k=0 |
|
|
|
|
|
где βk ,п |
=αп ∞∫ρxy (τ +τm )ψn (τ ,αп )dτ ; |
|
|
|
(5.47) |
|
|
0 |
|
|
|
|
|
βk ,л |
=αл ∞∫ρxy (τm −τ )ψn (τm ,αл )dτ . |
|
|
|
(5.48) |
|
|
0 |
|
|
|
|
|
|
5.2. Задание на самостоятельную работу |
|
|
|||
1. |
Для заданного ортогонального базиса, вида корреляционной функции и |
|||||
показателя колебательности μ определить коэффициенты разложения |
{βk |
}k =0 ,...m . По- |
||||
строить графическую зависимость {βk }k =0 ,...m . |
|
|
|
|
||
2. |
Построить зависимость δ (1)(m / χ,μ)= |
∞ |
( m / χ,μ ) . Значение пара- |
|||
|
|
|
∫ρx2 (τ )μ(τ )dτ |
|
|
|
|
|
|
0 |
|
|
|
метра χ выбрать произвольно, |
μ = 0 ÷ 5 . Убедиться в справедливости равенства |
|||||
Парсеваля (см. лаб. работу 1). |
|
|
|
|
|
|
3. |
Построить зависимость δ (2 )(χ / m,μ), |
m = 2 ÷6 , μ = 0 ÷ 5 (Результаты |
||||
представить аналогично результатам таблицы 5.9). Определить количество локальных минимумов δ(χ / m,μ), их численные значения χopt и соответствующие им значения
погрешностей.
4.Построить зависимость δmin(3 ) (μ / m,χopt ) и δmin(1) (m / μ,χopt ).
5. |
Сравнить |
результаты |
оценки |
δ1(3 )(μ / m,χ1 ), |
δ2(3 )(μ / m,χ2 ), |
δ1(1)(m / μ,χ1 ), δ2(1)(m / μ,χ2 ) с соответствующими минимальными оценками погреш- |
|||||
ности. Значение параметра χ1 определяется по таблице 5.10-5.13, а χ2 |
- по таблицам |
||||
5.13-5.14. |
|
|
|
|
|
6.Построить модели корреляционной функции, соответствующие выраже-
нию 5.16, для λ = 1, μ = 5, χ1 , χ2 , χopt , m = 5,10 .
7.Оформить отчет.
5.3.Содержание отчёта
1.Цель работы.
2.Задание.
3.Исходный текст программы, написанной в MathCad.
70
4.Результаты выполнения работы в мат. пакете MathCad.
5.Ортогональная модель корреляционной функции в заданном ортогональ-
ном базисе.
{βk }k =06.,...m . Аналитическое выражение для оценки коэффициентов разложения
7.Аналитические выражения для оценки χ1 и χ2 .
8.Графические зависимости δ (1)(m / χ,μ) (пункт 2).
9.Графические зависимости δ (2 )(χ / m,μ) (пункт 3).
10.Графические зависимости δmin(3 ) (μ / m,χopt ) и δmin(1) (m / μ,χopt ) (пункт 4).
11.Графические зависимости δ1(3 )(μ / m,χ1 ), δ2(3 )(μ / m,χ2 ), δ1(1)(m / μ,χ1 ),
δ2(1)(m / μ,χ2 ) (пункт 5).
12.Графики моделей корреляционной функции (пункт 6).
13.Выводы.
Пример выполнения вычислительного практикума 5 приведен в Приложении
11.
5.4.Контрольные вопросы
1.Какие параметры входят в ортогональную модель корреляционной
функции?
2.Как параметры ортогональной модели влияют на вид оцениваемой корреляционной функции?
3.Как количество локальных экстремумов погрешности аппроксимации связаны с m и μ ?
4.Какое условие положено в основу приближенного определения параметра масштаба?
5.Каким образом изменится длительность ортогональной функции при увеличении параметра масштаба?
6.Как изменится численное значение параметра масштаба при увеличении числа членов разложения ряда?
7.Как изменится численное значение параметра масштаба при увеличении показателя колебательности корреляционной функции?
71
6. АППРОКСИМАЦИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ ОРТОГОНАЛЬНЫМИ ФУНКЦИЯМИ С УЧЕТОМ УСЛОВИЯ НОРМИРОВКИ
Цель работы: изучение метода и приобретение практических навыков при аппроксимации корреляционных функций случайных процессов ортогональными функциями с учетом условия нормировки.
6.1. Теоретические основы лабораторной работы
Одной из отрицательных черт аппроксимации корреляционной функции ортогональными функциями является то, что её основное свойство
^ |
m |
ψk (0,α)≠σx2 |
|
K a (0)=σx2 |
∑βk |
(6.1) |
k =0
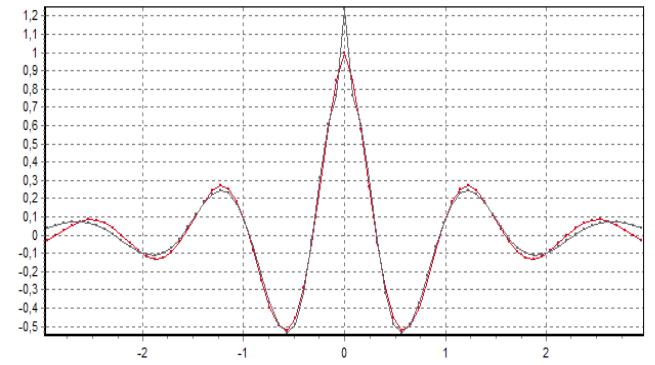
при произвольной величине α не выполняется при конечном m [21] (см. рис. 6.1), т.е. не выполняется условие нормировки.
Рисунок 6.1 - Аппроксимация КФ 5 модели с μ = 5 ортогональными функциями Лагерра - m =15 , α = 4,899
Для обеспечения условия (6.1) аналитическое выражение Kx (τ ) можно искать в виде:
^ |
(τ )=σx2 |
m |
ψk (τ ,α) |
Ka |
∑νk |
||
|
|
k =0 |
|
72
