Файловый архив студентов. Файловый архив студентов.
1262 вуза, 4625 предмета.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Самарский национальный исследовательский университет им. ак. С.П. Королёва (бывш. СГАУ, СамГУ)
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Vychislitelny_praktikum

.pdf
Скачиваний:
12
Добавлен:
16.03.2015
Размер:
7.27 Mб
Скачать
☆

При t ji = t0 = const исследователь имеет дело с регулярной временной по-

следовательностью - регулярным временным рядом, примеры реализаций которого приведены на рис. 10.4.

Рисунок 10.4 - Примеры реализации регулярных случайных последовательностей

Выражения для оценки КФ при анализе последовательностей в зависимости от оператора усреднения примут вид:

K^ xyi (J

K^ (J

xy j

^

Kxyср(J

τ)=

1

N o

o

 

∑x ji

y j ,i+J ;

 

 

 

 

 

 

N j=1

 

 

 

 

τ)=

 

1

 

M−J o o

 

 

 

∑xji y j,i+J ;

(10.11)

 

M −J −

 

 

 

1 i=1

 

τ)=

1

 

 

N M−J o

o

 

 

 

 

 

∑∑x ji y j ,i+J .

 

 

 

 

 

 

 

 

N( M −J −1) j=1 i=1

 

Следует отметить, что при аппроксимации ВКФ с помощью ЭВМ не важно, какая характеристика аппроксимируется - t -текущая, j - текущая или средняя, - подход

один и тот же.

В тех случаях, когда исследователь располагает только одной реализацией (j = const), при проведении корреляционного анализа, как правило, используется

мультипликативный алгоритм, инвариантный к закону распределения случайного процесса [55]:

При этом интервал дискретизации корреляционной функции, как правило, выбирают равным τ = t0 .

Значение интервала дискретизации τ зависит от вида корреляционной функции, значения её параметров, допустимой погрешности δ и способа восстановления

123

ρ′(τ )=Фx [ρx (τ )].

корреляционной функции между узлами. Минимальное количество требуемых ординат корреляционной функции Jmax при линейной интерполяции и различных погрешностях её восстановления представлено в таблице 10.1 [21].

Количество ординат корреляционной функции и интервалы дискретизации Таблица 10.1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ρx (τ )

 

 

 

 

 

 

τ

 

 

δ = 0,02

 

 

δ = 0,05

 

 

 

 

 

 

 

 

τ

 

Jmax

 

τ

 

 

Jmax

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

δ

 

 

0,4

 

 

 

 

 

0,632

 

 

 

 

e−λ

 

τ

 

 

 

 

 

 

 

 

 

 

 

 

8

 

 

 

 

 

 

9

 

 

 

 

 

 

6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

λ

 

 

 

λ

 

 

 

λ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

e−λ

 

τ

 

(1 + λτ

 

 

)

 

 

 

 

 

 

8δ

 

 

0,4

 

13

 

 

0,632

 

9

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

λ

 

 

 

λ

 

 

 

 

 

 

λ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

e−λ

 

τ

 

(1 − λτ

 

)

 

 

 

 

 

 

8δ / 3

 

0,23

19

 

 

0,365

 

13

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

λ

 

 

 

λ

 

 

 

 

 

 

λ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

e−λ

 

τ

 

(1 + λτ

 

+ λ2τ 2

/ 3)

 

24δ

 

0,693

10

 

 

1,095

 

7

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

λ

 

 

 

λ

 

 

 

 

 

 

λ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

e−λ

 

τ

 

cosω τ ,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

1

8δ

1

0,16

 

μ

 

1 0,4

 

 

μ

 

 

 

 

 

 

 

 

 

 

λ

 

47

 

 

47

 

 

−λ

τ

 

 

 

λ

μ

2

+1

λ

μ

2

+1

 

 

λ

 

2

 

 

 

 

e

 

 

 

 

 

 

±

 

 

 

 

 

 

 

2π

μ

 

+1

 

2π

 

 

 

 

 

cosω0τ

ω0

sinω0τ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Для проверки качества генерирования ПСП представляется перспективным использование фазовых портретов. Под фазовым портретом будем понимать графическую зависимость, построенную в координатах: ρx (τ ) и ρ′x (τ ) :

(10.12)

Следует отметить, что каждому типу корреляционных функций соответствует свой, уникальный фазовый портрет (см. рис. 10.5). На практике при построении фазового портрета вместо значения производных корреляционных функций возможно определение её приращений на заданном интервале.

Рассмотрим алгоритм построения КФ по параметрам модели спектральной плотности мощности (см. лабораторную работу 7).

Для этого представим модель СПМ в виде

2

m

m

ψ k

 

(10.13)

Sax (ω)=σ x

∑Ck

ψ k (ω,α)1(ω)+ ∑Ck

(−ω,α)1(− ω) ,

 

k =0

k =0

 

 

 

где коэффициенты разложения Ck определяются выражением (7.24) (см. таблицы 7.6

– 7.7).

Подставив в выражение (7.2) выражение (10.13), выполнив преобразования, получим:

m

ReWk (jτ ).

 

Kax (τ )= 2σ x2 ∑Ck

(10.14)

k =0

Следует отметить, что в автоматизированной системе для унификации (см. лабораторную работу 11) Ck являются коэффициентами разложения вещественной части спектра, совпадающей с СПМ.

124

 

0,00

 

 

 

 

 

 

 

 

 

 

 

0,00

 

 

 

 

 

 

 

 

 

-0,050,00

0,20

0,40

0,60

0,80

1,00

 

 

 

0,00

0,20

0,40

0,60

0,80

1,00

 

-0,10

 

 

 

 

 

 

 

 

 

 

 

-0,04

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

-0,15

 

 

 

 

 

 

 

 

ρ'(τ) -0,08

 

 

 

 

 

 

 

 

ρ'(τ) -0,20

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

-0,25

 

 

 

 

 

 

 

 

 

 

 

-0,12

 

 

 

 

 

 

 

 

 

-0,30

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

-0,35

 

 

 

 

 

 

 

 

 

 

 

-0,16

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ρ(τ)

 

 

 

 

 

 

 

 

 

ρ(τ)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

а) ρx (τ )= e−λ τ , λτ = 0,4

 

 

б) ρx (τ )= e−λ τ (1+λτ ), λτ = 0,4

 

 

 

0,10

 

 

 

 

 

 

 

 

 

 

0,00

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0,00

 

 

 

 

 

 

 

 

 

 

0,00

0,20

 

0,40

 

0,60

0,80

1,00

-0,20

0,00

0,20

0,40

0,60

0,80

1,00

 

 

 

-0,05

 

 

 

 

 

 

 

 

 

-0,10

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ٛ'ٛٛٛ

-0,20

 

 

 

 

 

 

 

ρ'(τ) -0,10

 

 

 

 

 

 

 

 

 

-0,30

 

 

 

 

 

 

 

 

 

 

-0,15

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

-0,40

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

-0,50

 

 

 

 

 

 

 

 

 

 

-0,20

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ρ(τ)

 

 

 

 

 

 

 

 

 

ٛٛٛٛ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

в) ρx (τ )= e−λ τ , λτ = 0,4

 

 

г) ρx (τ)=e−λ τ (1+λτ ),λτ =0,4

 

 

 

 

 

 

 

0,15

 

 

 

 

 

 

 

 

 

0,20

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0,10

 

 

 

 

 

 

 

 

 

0,10

 

 

 

 

 

 

 

 

 

 

 

0,05

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0,00

 

 

 

 

 

 

 

 

 

0,00

 

 

 

 

 

 

 

-0,50

 

-0,25-0,050,00

0,25

0,50

0,75

1,00

-0,75

-0,50

-0,25

0,00

0,25

0,50

0,75

1,00

ρ'(τ)

 

 

-0,10

 

 

 

 

ρ'(τ)

 

 

 

 

-0,10

 

 

 

 

 

 

 

 

 

 

-0,15

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

-0,20

 

 

 

 

 

 

 

 

 

-0,20

 

 

 

 

 

 

 

 

 

 

-0,25

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

-0,30

 

 

 

 

 

 

 

 

 

-0,30

 

 

 

 

 

 

 

 

 

 

-0,35

 

 

 

 

 

 

 

 

 

-0,40

 

 

 

 

 

 

 

 

 

 

 

 

ρ(τ)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ρ(τ)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

д)

ρ

x

(τ)

=e−λ τ

cosω τ, μ =3

 

 

е) ρ

x

(τ)= e−λ τ

cosω τ, μ = 5

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

0

 

 

 

 

 

 

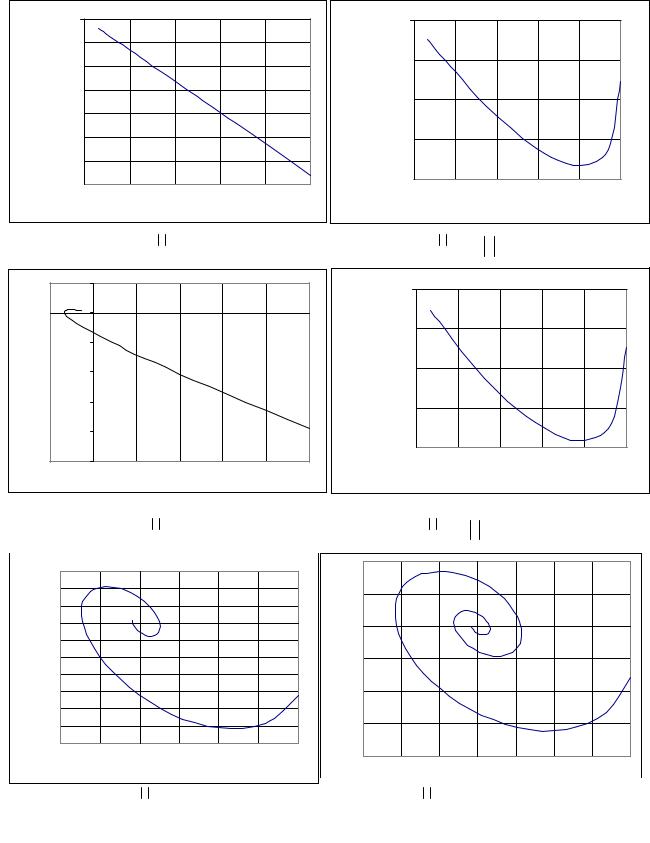
Рисунок 10.5 – Фазовые портреты моделей КФ

Для выполнения вычислительного практикума необходимо изучить автоматизированную систему корреляционно-спектрального анализа в ортогональных базисах

125

(см. Приложение 17). Руководство пользователя приведено в Приложении 18, а формат вводимых и выводимых данных – в Приложении 19.

Основные алгоритмы, положенные в основу её работы, подробно описаны в лабораторных работах 2-9.

Следует отметить, что с помощью автоматизированной системы возможен кор- реляционно-спектральный анализ экспериментальных данных. Для этого необходимо ввести данные в соответствующем формате (см. Приложение 19), используя экранную форму «Filter setting». Пример корреляционно-спектральной обработки экспериментальных данных (см. Приложение 21) приведен в Приложении 20.

10.2. Задание на самостоятельную работу

1. Сгенерировать временной ряд с заданным видом корреляционной функции и со следующими параметрами - M = ent[τk max / τ], N= 5000 , δ = 0,02 .

2.Построить КФ и её фазовый портрет, сравнить с теоретическими кривы-

ми.

3.Для заданного ортогонального базиса определить параметры модели и погрешность аппроксимации.

4.Определить интервалы корреляции, сравнить с теоретическими интервалами, найти относительную погрешность оценивания интервалов корреляции.

5.Найти корректирующие коэффициенты, обеспечивающие условие нормировки ортогональной модели КФ, и построить модель КФ.

6.Определить интервалы корреляции, сравнить с теоретическими интервалами, найти относительную погрешность оценивания интервалов корреляции.

7.Построить модель спектральной плотности мощности.

8.Определить экстремальную частоту, значение СПМ в точке, соответствующей экстремальной частоте, и эквивалентную ширину спектра мощности. Сравнить полученные результаты с теоретическими характеристиками, найти относительную погрешность оценивания обобщенных характеристик.

9.Передать действительную компоненту СПМ в подсистему аппроксимации составляющих СПМ и построить ортогональную модель действительной части СПМ.

10.Построить КФ и сравнить с теоретической.

11.При исследовании других ортогональных базисов необходимо повторить пункты 3 – 10.

12.Построить КФ «идеального» полосового шума.

13.Построить ортогональную модель КФ.

14.Построить ортогональную модель спектральной плотности мощности.

15.Пункты 13 – 14 повторить и выбрать наилучший базис.

10.3.Содержание отчёта

1.Цель работы.

2.Задание.

3.Результаты выполнения работы в автоматизированной системе, представленные в виде экранных форм.

4.Выводы.

126

10.4.Контрольные вопросы

1.Какой метод положен в основу генерации временных рядов с заданным видом корреляционной функции?

2.Из каких соображений выбирают численное значение интервала дискретизации временного ряда?

3.Какой метод фильтрации применен в лабораторной работе?

4.Чем отличается метод имитационного моделирования от обработки экспериментальных данных?

5.С какой целью строятся фазовые портреты моделей?

6.Какая часть фазового портрета наиболее информативна?

7.Как по виду фазового портрета определить характер корреляционной функции: монотонная, колебательная?

8.Что из себя представляет «идеальный полосовой шум»?

127

11. ПОСТРОЕНИЕ ОРТОГОНАЛЬНЫХ МОДЕЛЕЙ ВЗАИМНЫХ КОРРЕЛЯ- ЦИОННО-СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК

С ПОМОЩЬЮ АИС

Цель работы: изучение методов и приобретение практических навыков построения ортогональных моделей взаимных корреляционноспектральных характеристик временных рядов.

11.1.Теоретические основы вычислительного практикума

Впредлагаемой лабораторной работе решаются основные задачи взаимного корреляционно-спектрального анализа временных рядов.

Для ее выполнения необходимо изучить автоматизированную систему корре- ляционно-спектрального анализа в ортогональных базисах (см. Приложение 17).

Основные алгоритмы, положенные в основу её работы, подробно описаны в лабораторных работах 2, 3, 5, 6, 9, 10, 11.

Исследование алгоритмов проводится методом имитационного моделирования на ЭВМ с помощью АИС (см. Приложение 17).

Исходными данными для АИС являются коррелированные временные ряды с заданными корреляционными характеристиками.

Самый простой вариант решения этой задачи заключается в генерировании ПСП с заданным видом корреляционной функции и её задержке на заданный временной интервал [21, 22, 23].

Вкачестве критерия качества генерирования ПСП можно также воспользоваться косвенным методом:

•оценить взаимную корреляционную функцию;

•аппроксимировать её заданным аналитическим выражением с параметрами, удовлетворяющими минимуму квадратической погрешности аппроксимации;

•сравнить найденные параметры модели с требуемыми значениями параметров корреляционной функции [21].

Вторым методом косвенной проверки качества генерирования двух процессов с заданным видом взаимной корреляционной функции является применение фазовых портретов [22, 23]. Методика проверки заключается в выполнении следующих этапов:

•генерирования ПСП с заданным видом корреляционной и взаимной корреляционной функций;

•построения фазового портрета по взаимной корреляционной функции;

•сравнения полученного фазового портрета с эталонным, определенным по аналитической модели требуемой взаимной корреляционной функции.

Преимущество такого способа проверки качества генерирования заключается в простоте, наглядности и отсутствии необходимости решать аппроксимативную задачу. На рис. 11.1 - 11.2 приведены примеры фазовых портретов типовых моделей взаимных корреляционных функций. Для сравнения приведены результаты аппроксимации взаимных корреляционных функций соответствующими параметрическими моделями.

Следует отметить, что задача проверки качества подобным способом требует предварительного определения фазового портрета корреляционной функции для генерируемого процесса.

128

а) ρx (τ )= e−λ τ −τm , λ =1,τm =10

б) ρx (τ )= e−λ τ −τm (1 + λτ −τm ), λ =1,τm =10

в) ρx (τ )= e−λ τ −τm (1 − λτ −τm ) , λ =1,τm =10

Рисунок 11.1 - Взаимные корреляционные функции и фазовые портреты монотонных моделей

129

а ) ρ x (τ ) = e − λ τ −τ m cos ω 0 (τ − τ m ), λ = 1 , ω 0 = 5 , τ m = 10

б) ρx (τ )= e−λ τ −τm (cosω0 (τ −τm )+ λ / ω0 sinω0 (τ −τm ), λ =1, ω0 = 5,τm =10

в) ρ

x

(τ)=e−λ

 

τ−τm

 

(cosω

(τ −τ

m

)−λ / ω

sinω

(τ −τ

m

),λ =1,ω =5,τ

m

=10

 

 

 

 

 

0

 

0

0

 

0

 

Рисунок 11.2 - Взаимные корреляционные функции и фазовые портреты колебательных моделей

130

Эта задача также может быть реше-

 

 

 

 

o

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x(t)

на и методом фильтрации с использовани-

 

o

(t)

 

 

ем единственного источника

первичного

 

ν

W1 (jω)

 

сигнала (см. рис. 11.3).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Спектральные плотности мощности

 

 

 

 

 

 

 

 

 

o

 

 

 

и

o

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Генератор

 

 

 

 

сигналов x(t)

y(t) соответственно рав-

«белого»

 

 

 

 

ны:

 

 

 

 

 

 

 

 

 

 

 

 

шума

 

 

 

o

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y(t)

 

S

 

(ω)= S

 

 

W (jω)

 

2 ;

 

 

 

 

 

x

0

 

 

 

 

 

W2 (jω)

 

 

 

 

 

 

1

 

 

 

 

 

 

 

o

(t)

 

 

S

 

(ω)= S

 

W (jω)

 

2 ;

 

 

 

 

 

 

ν

 

 

S

 

y

 

 

0

 

2

 

 

 

 

 

(11.1)

 

 

 

 

 

 

 

(jω)= S W

(jω)W (− jω);

 

 

 

 

 

xy

 

 

 

 

 

 

 

 

 

 

 

0

1

2

 

Рисунок 11.3 - Генерирование коррелиро-

S

 

 

(jω)= S W

(− jω)W (jω),

 

 

 

yx

 

 

 

0

1

2

 

ванных ПСП с заданным видом

где W1 (jω), W2 (jω) - частотные характе-

корреляционных функций

ристики формирующих фильтров.

В работе [44] в Приложении 2 приведены выражения для импульсных переходных характеристик формирующих фильтров, а в Приложении 3 - соответствующие им корреляционные функции.

Рассмотрим алгоритм построения ВКФ по параметрам модели спектральной

плотности мощности (см. вычислительный практикум 7).

 

Обозначим

 

Sxy (jω)= ReSxy (jω)− jImSxy (jω).

(11.2)

Отсюда очевидно, что

S yx (jω)= ReSxy (jω)+ jImSxy (jω).

Запишем синфазную и квадратурную составляющие спектра:

Cxy (ω)= 2ReS(jω)= π1 ∞∫[Kxy (τ )+ K yx (τ )]cosωτdτ ,

0

Qxy (ω)= 2 ImSxy (jω)= π1 ∞∫[K yx (τ )− Kxy (τ )]sinωτdτ .

0

Воспользовавшись обратным преобразованием Фурье, получим:

(11.3)

(11.4)

(11.5)

Kxy (τ )+ K yx (τ )= 2∞∫Cxy (ω)cosωτdω ;

(11.6)

 

0

 

K yx (τ )− Kxy (τ )= 2∞∫Qxy (ω)sinωτdω .

(11.7)

 

0

 

Из (11.6) и (11.7) следует, что

 

Kxy (τ )=∞∫Cxy (ω)cosωτdω −∞∫Qxy (ω)sinωτdω ,

(11.8)

0

0

 

Kxy (τ )= 2∞∫Re Sxy (ω)cosωτdω − 2∞∫Im Sxy (ω)sinωτdω .

(11.9)

0

0

 

Учитывая тот факт, что спектральная плотность мощности – функция комплексной переменной, будем аппроксимировать вещественную и мнимую части раздельно. При использовании в качестве аппроксимирующих функций ортогональные функции получим:

131

Re Saxy (ω)= ∑mRe

βk Reψk Re (ω,αRe );

 

 

 

 

 

 

k =0

 

 

 

Im Saxy (ω)= ∑mIm

βk Imψk Im (ω,αIm ),

где

 

 

 

 

 

k =0

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

∞

(u)ψ k Re(u,αRe )du;

βk Re

=

 

 

 

 

 

 

 

 

 

 

 

 

 

∫Re Sxy

 

ψk Re

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

∞

(u)ψ k Im(u,αIm )du.

 

βk Im

=

 

 

 

 

 

 

 

 

∫Im Sxy

 

 

ψ

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

k Im

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Представим взаимную корреляционную функцию в виде:

(11.10)

(11.11)

(11.12)

∞ m

 

(ω,αRe )cosωτdω −

Kaxy (τ )= 2∫∑Re βk Reψk Re

0 k =0

 

(11.13)

∞ m

 

(ω,αIm )sinωτdω.

− 2∫∑Im βk Imψk Im

0 k =0

 

 

Воспользовавшись формулами Эйлера, выражение (11.13) приведем к виду:

K

 

(τ)=mRe β

 

(W

(− jτ)+W

(jτ))−

1

mIm β

 

(W

(− jτ)−W

(jτ)).

(11.14)

axy

k Re

 

k Im

 

∑

k Re

k Re

 

 

∑

k Im

 

k Im

 

 

 

 

k=0

 

 

 

 

j k=0

 

 

 

 

 

 

где Wk (jτ ) – преобразование Фурье ортогональных функций (см. таблицу 4.2), в ка-

честве аргумента которых используется jτ .

 

 

 

 

 

 

Из выражения (11.14), выполнив преобразования, окончательно получим

 

 

mRe

 

ReWk Re (jτ )

mIm

 

 

 

 

 

 

 

 

Kaxy (τ )= 2 ∑βk Re

+ ∑βk Im ImWk Im (jτ ) .

 

 

(11.15)

 

 

k =0

 

 

k =0

 

 

 

 

 

 

 

 

Выражения для оценки ReWk Re (jτ )

и ImWk Im (jτ )

определяются для ортого-

нальных функций соответственно формулами:

•Лагерра, Лежандра, Дирихле, Якоби (α,0) - (4.6), (4.7);

•Сонина-Лагерра (1) - (4.11), (4.12);

•Сонина-Лагерра (2) - (4.14), (4.15);

•Якоби (0,1) - (4,17), (4.18);

•Якоби (0,2) - (4,29), (4.21).

Вуказанных формулах необходимо заменить аргументы: ω на τ .

Втаблице 11.1 и 11.2 приведены выражения для определения ReWk Re (jτ ) и

ImWk Im (jτ ) в указанных ортогональных базисах.

132

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности