Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Самарский национальный исследовательский университет им. ак. С.П. Королёва (бывш. СГАУ, СамГУ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Vychislitelny_praktikum

.pdf

Скачиваний:

Добавлен:

16.03.2015

Размер:

7.27 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 3111 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

ρx (τ )		−
ρx (τ )

	τk max

Рисунок 9.1 - Максимальный интервал корреляции

Аналитические выражения τk max для типовых моделей ρx (τ ,λ,ω0 ) приведены в таблице 9.1.

Максимальные интервалы корреляции типовых моделей

корреляционных функций

Таблица 9.1

№

Вид модели ρx (τ ,λ,ω0 )

= 0,01

= 0,02

= 0,05

e−λ

4,61 λ

3,92 λ

3 λ

e−λ

(1 + λ

)

6,64 λ

5,84 λ

4,75 λ

e−λ

(1 − λ

)

6,27 λ

5,40 λ

4,14 λ

λ2τ 2

−λ

8,03 λ

7,14 λ

5,92 λ

1 + λ

−λ

ω τ

)

4,61 λ

3,92 λ

3 λ

cos(

−λ

sin(ω0

4,61 λ

3,92 λ

3 λ

cos(ω0τ )+

ω0

)

−λ

sin(ω0

4,61 λ

3,92 λ

3 λ

cos(ω0τ )−

ω0

)

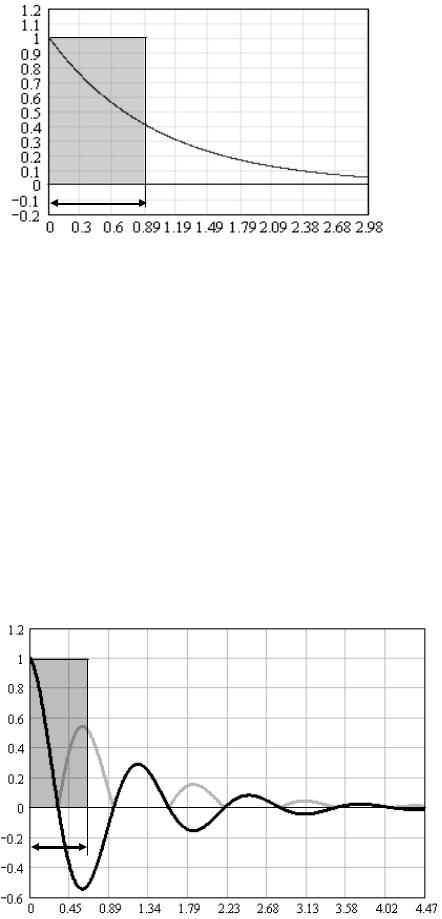
Часто под интервалом корреляции понимается основание прямоугольника с высотой, равной единице, площадь которого равновелика площади фигуры, определяемой нормированной КФ [48, 49]:

τk(2 ) = ∞∫ρ(τ )dτ.

(9.2)

Графическая интерпретация величины τk(2 ) дана на рисунке 9.2.

103

ρ x (τ )

τ k( 2 )

Рисунок 9.2 - Интервал корреляции τk(2 )

Отметим, что для некоторого класса процессов τk(2 ) = 0 (например, для колеба-

тельных моделей, площадь положительной и отрицательной части которых равна), что свидетельствует об отсутствии корреляции между сечениями процесса. Однако это не так, корреляция есть, и это подтверждает τk max >0 . Следовательно, при оценке

длительности существования корреляционной функции интервал корреляции τk(2 ) це-

лесообразно применять лишь при анализе случайных процессов с монотонными корреляционными функциями.

Для устранения отмеченного недостатка в [48] были предложены следующие определения интервалов корреляции:

τk(3 ) = ∞∫		ρx (τ )	dτ ,	(9.3)
τk(3 ) = ∞∫		ρx (τ )	dτ ,	(9.3)
	0
	∞
τk(	4 ) = ∫ρ2 x (τ )dτ .			(9.4)
	0
Графическая интерпретация величины τk(3 ) приведена на рисунке 9.3.

ρx (τ )

τ k(3)

τ τ (3 )

Рисунок 9.3 - Интервал корреляции k

104

Анализ выражений (9.2) и (9.3) показывает, что аналитическая оценка длительности существования корреляционной функции для колебательных моделей затруд-

нена. От этого недостатка свободно определение τk(4 ). Поэтому, несмотря на то, что τk(4 ) дает заниженные результаты, в технических приложениях он применяется значительно чаще, чем τk(3) . Значения интервалов корреляции τk(2 ) и τk(4 ) для типовых моделей корреляционных функций приведены в таблице 9.2.

Интервалы корреляции для типовых моделей корреляционных функций

Таблица 9.2

№

Вид модели ρx (τ ,λ,ω0 )

τk(2 )

τk(4 )

e−λ

2λ

e−λ

(1 + λτ

)

4λ

e−λ

(1 − λτ

)

4λ

−λ

λ2τ 2

+ λ

3λ

4λ

−λ

cos(ω0τ )

2λ2 +ω02

λ2

+ ω02

4λ (λ2

+ω02 )

−λ

2λ

5λ2 + ω02

cos(ω0τ )+

ω0

sin(ω0

)

4λ (λ

)

+ ω0

−λ

cos(ω0τ )−

ω0

sin(ω0

)

4λ

В таблице 9.3 показано, во сколько раз τk max

больше τk(2 ) и τk(4 ) (

= 0,05 ).

№

Вид модели ρx (τ ,λ,ω0 )

Таблица 9.3

τk max /τk(2 )

τk max /τk(4 )

e−λ

(1 + λ

)

2,375

3,8

e−λ

(1 − λτ

)

∞

16,56

λ2τ 2

−λ

+ λτ

2,22

3,38

2(1 + μ2 )

−λ

cos(ω0τ )

3(1 + μ2 )

2 + μ2

105

1,5(1 + μ2 )

12(1 + μ2 )

−λ

cos(ω τ )+

sin(ω

)

(5 + μ

)

ω0

−λ

∞

cos(ω0τ )−

ω0

sin(ω0

)

Отсюда видно, что τk(2 ) и τk(4 ) дают сильно заниженный результат по сравнению

с τk max .

9.1.1. Интервалы корреляции

Определив параметры модели корреляционной функции в ортогональном базисе в виде (5.13) и воспользовавшись определением корреляционных характеристик, можно найти их аналитические выражения, содержащие только параметры модели.

Так выражение для оценки τ^ (k2 ) примет вид:

^	m	∞	m	(0).
τ (k2 )≈ ∑βk ∫ψk			(τ ,α)dτ =∑β kWk	(0).	(9.5)
	k =0	0	k =0

Аналитические выражения τk(2 ) для различных ортогональных базисов приведены в таблице 9.4.

Интервалы корреляции в различных ортогональных базисах

Таблица 9.4

№

ψk (τ ,γ / α)

τ^ (2 )

Lk (τ ,α)

∑(−1) bk .

α k =0

(1) τ γ

)

[(k + 1)mod 2]

∑

Lk (

k + 1

k =0

(2 ) τ γ

)

[(k + 2)div 2]

∑

Lk (

k =0 (k + 1)(k + 2)

Legk (τ,α)

1 ∑bk

α k =0

(2k +1)

Dk (τ ,α)

∑m

(−1)k

(k +1)

α k =0

2 m

∑

P(−1 2,0)(τ,γ)

k =0

(4k +1)

Pk(1 2,0)(τ,γ)

∑

k =0 (4k + 3)

( 1,0 )

τ γ

( ,

)

∑ k

(k +1)

k =0

( 2,0 )

τ γ

m b

( ,

)

∑ k

(2k + 3)

k =0

106

	P( 0,1) (τ,γ)			1		m	bk		[(k + 1)mod 2]
10				1		∑	bk
10						∑		2
	k				γ k =0 (k + 1)
					γ k =0 (k + 1)
		4		m			b (− 1)k		2
11	Pk( 0,2 ) (τ,γ)			∑			k			[(k + 2)div 2]
11	Pk( 0,2 ) (τ,γ)		γ	∑			2		2	[(k + 2)div 2]
			γ	k =0 (k + 1) (k				+ 2)

Конечное число членов разложения ряда (5.13) m приводит к погрешности от смещенности в определении интервала корреляции, которую оценим в соответствии с выражением:

γсм =

τ^ (2 )−

τ (2 )

(9.6)

τ (2 )

Определим погрешность от смещенности, в качестве примера, для ортогональ-

ного базиса Лагерра (частное сообщение Волкова И.И.).

Для НКФ ρx1(τ ) = e−λ

τk(2 ) =

, а коэффициенты разложения [22, 23]

λ −α /

2 k

(9.7)

+α /

λ +α / 2

Подставив выражение (9.3) в (9.1), получим

− λ m+1

/ 2

^ (2 )

−α / 2

−

/ 2

+ λ

τ k

∑

( −1 )

(9.8)

λ +α / 2

k =0

+α / 2

Погрешность от смещенности в соответствии с (9.2) примет вид:

γсм

α / 2 −

λ m+1

(9.9)

= −

α / 2 +

При произвольном значении α γсм может принимать достаточно большое зна-

чение.

Определим α в результате решения уравнения β0 = 1 [22, 23]. Отсюда

α = 2λ .

(9.10)

Погрешность от смещенности в этом случае: γсм = 0 .

Таким образом, выбор параметра α для данной модели дает возможность получить принципиально нулевую погрешность.

Для второй типовой модели ρx 2 (τ ) = e−λ

(1 + λ

) τk(2 )

λ −α / 2

k −1

λ −α / 2

2λ +α / 2

− k

αλ

βk

λ +α / 2

(λ +α / 2)

λ +α / 2

^ (2 )

α / 2 −λ m+1

(m +1)α

α / 2 −λ m

τ k

−

(α / 2 + λ)2

α / 2 + λ

α / 2

− λ m

(m +1)αλ

γсм

= −

α / 2 − λ

α / 2 + λ α / 2

+ λ

2(α / 2 + λ)

(9.11)

(9.12)

(9.13)

107

Найдем α из условия β0 = 1 - α = 2λ( 2 − 1) [22, 23]. Подставив

получим:		(m − 1)
			m
γсм = −			(−1) .
	2(	2 + 1)m+1

Если m=1 γсм =0. При m→∞ γ→0.

Погрешность γсм , как следует из (9.14), достигает минимума при

n =

1 +

2 ), γсмmin =

2 )< 1.

ln(1 +

2e(3 + 2

2 )ln(1 +

Для третьей типовой модели ρx3 (τ ) = e−λ

(1 − λτ

) τk(2 )=0,

βk =

α 2 / 2

λ −α / 2 k

2kλ

λ −α / 2 k −1

λ +α

(λ +α / 2)

λ +α / 2

(λ +α / 2)

/ 2

^ (2 )

(m +1)α

α / 2 −

λ m

τ k

(λ

+α / 2)2

α / 2 +

^ (2 )

≠ 0 .

Найдем α

Нетрудно видеть, что при произвольном α τ k

β0 = 1 - α = 2λ(1 +

2 )[22, 23].

Величина оценки интервала корреляции в этом случае будет равна:

(2 )

m + 1

λ (

2 + 1)m+1

α в (9.13),

(9.14)

(9.15)

(9.16)

из условия

(9.17)

Как следует из (9.17) при m→∞ τ^ → 0 , то есть оценка стремится к идеальной.

Для типовой модели ρ

(τ )= e−λ

cosω τ τ (2 )

λ2

+ω2

x 5

α / 2

−α / 2 − jω0

α / 2

−α / 2 + jω0

βk

= λ +α / 2 − jω

+α / 2 + jω

λ +α / 2 + jω

+α / 2 + jω

, (9.18)

^ (2)

1 1

α/ 2

−λ+ jω0

m+1

α / 2 −λ− jω0

m+1

τ k

= λ2 +ω2 −

2 λ

− jω

+λ− jω

+λ+ jω

(9.19)

α/ 2

α/ 2+λ+ jω

Погрешность от смещенности равна:

α / 2 −λ + jω0

m+1

α / 2

−λ − jω0

m+1

γсм

/ 2 +λ − jω

α / 2

+λ + jω

(9.20)

= 2λ (λ + jω0 )

+(λ − jω0 )

Найдем α из условия

β0 = 1 - α = 2

λ2

+ω02

[22,23].

В результате получим:

m+1

= jm +1

ω0

[λ + jω0 + (−1)m+1 λ − (−1)m+1 jω0 ]

γсм

λ +

+ω2

(9.21)

2λ

λ2

Величина погрешности γсм , как видно из (9.21), зависит от того, четным или

нечетным будет число m. При m=2n, получим:

108

см = (−1)

n+1

2n+1

n+1 ξ

2n+1

(9.22)

λ +

+ω2

= (−1)

1−ξ2

1−ξ 2

λ2

а при нечетном m=2n+1:

γсм = (−1)

ω0

2(n+1)

= (−1)

n+1

2(n+1)

(9.23)

λ +

1 + 1 −ξ

ω0

+ω0

гдеξ =

, 0

≤ ξ ≤ 1.

λ2

+ω2

Формулы (9.22) и (9.23) можно представить в виде:

= (−1)

n+1

1 −ψ

−ψ

см

+ψ

(9.24)

n+1 1

−ψ

n+1

= (−1)

см

1 +ψ

где ψ =

, 0 ≤ψ ≤ 1.

λ2 +ω

Анализ погрешности от смещенности оценки τ^ (k2 )

показывает, что при n→∞

γсм → 0 . Однако при четном m погрешность от смещенности стремится к бесконеч-

ности при λ→1 (ψ→0), то есть при большом показателе колебательности корреляционной функции. Поэтому, с точки зрения повышения точности необходимо выбирать m=2n+1. Аналогичные рекомендации можно сделать и для других колебательных моделей корреляционных функций.

Воспользовавшись определением погрешности аппроксимации корреляционной функции (μ(τ )= 1)

∞	m
= ∫K x2 (τ )dτ − Am2	∑βk2	ψk	2	(9.25)
= ∫K x2 (τ )dτ − Am2	∑βk2	ψk	2	(9.25)
0	k =0
и выражением (9.4), в качестве оценки интервала корреляции				можно принять выра-

жение:

τk(4 ) ≈ ∑βk2 ψ k 2 . (9.26)

k =0

Эта оценка будет тем точнее, чем меньше квадратическая погрешность аппроксимации корреляционной функции моделью вида (5.13). Заметим, что анализ этой погрешности и рекомендации по выбору оптимальных значений параметров модели представлен в лабораторной работе 5.

9.1.2. Оценка моментов корреляционных функций
Определив начальный момент n-го порядка в виде
μn = ∞∫τ n ρx (τ )dτ ,	(9.27)
0

109

можно показать, что при аппроксимации корреляционных функций ортогональными функциями Лагерра [22, 23]

μn =ϕn (α)∑m (− 1)k cnk βk .	(9.28)
k =0

Рекомендации по выбору параметров модели α, m и βk аналогичны рекомен-

дациям при определении интервала корреляции τ^ (k2 ) . Выражения для первых четырёх

моментов представлены в таблице 9.5.

К определению моментов корреляционной функции

		Таблица 9.5
μn	ϕn (α)	cnk
μ0	2/α	1
μ1	α2	1+2k
μ1	4/
μ2	α3	1+2k+2k2
μ2	16
μ3	α4	3+8k+6k2+4k3
μ3	32/

С учетом (9.21) выражения для корреляционных моментов в ортогональном базисе Лежандра и Дирихле равны:

μn

= ∑βk

n!n+1 ∑Cks Cks+s

(− 1)

n+1 ,

k =0

α s=0

(2s + 1)

s+1

(− 1)s

μn = ∑βk

(− 1)

∑Ck

Ck +s+1

n+1

(s +

n+1

k =0

s=0

9.1.3. Оценка эквивалентной ширины спектра мощности случайного процесса

(9.29)

(9.30)

Наиболее часто для процессов, у которых спектральная плотность мощности сосредоточена вблизи нулевой частоты (рис. 9.4 а), Δωэ определяют в виде:

		∞∫Sx (ω)dω			2
ωэ	=	0		=	σx	.	(9.31)
		Sx	(0)		2Sx (0)

Если основная мощность процесса сосредоточена вблизи экстремальной частоты спектральной плотности мощности ωэ (см. рис. 9.4 б), а не в нуле, выражение для оценки эквивалентной ширины примет вид:

ωэ′ =ωэ +	ωэ / 2 .	(9.32)
Выражения	для экстремальной частоты и эквивалентной ширины	спектра

мощности для типовых моделей корреляционных функций представлены в таблицах 9.6 и 9.7 соответственно.

110

а) б) Рисунок 9.4 - Эквивалентная ширина спектра мощности

			Экстремальные частоты
					Таблица 9.6
	№	ρx (τ )			ωэ
1		e−λ\|τ\|			0
2		e−λ\|τ\| (1 + λ \|τ \|)			0
3		e−λ\|τ\| (1 − λ \|τ \|)			α
4		e−λ\|τ\| (1 + λ \|τ \| +λ2τ 2 / 3)			0
5		e−λ\|τ\| cosω0τ			2ω0 ω02 + λ2 − (ω02 + λ2 )

6		e−λ\|τ\| (cosω0τ + λ / ω0		sinω0 \|τ \|)	ω02 − λ2

7		e−λ\|τ\| (cosω0τ − λ / ω0		sinω0 \|τ \|)	ω02 + λ2
		Эквивалентная ширина спектра мощности
					Таблица 9.7
	№			ωэ′ = ωэ +	ωэ′
	КФ			ωэ′ = ωэ +	2
					2
	1			πλ
				2
	2			πλ
				4
	3			λ(2 2 + 9π )
				4
	4			3πλ
				16
	5	ωэ +	π[λ2	+ ( ωэ −ω0 )2 ][λ2 + ( ωэ + ω0 )2 ]
		ωэ +		4λ(λ2 + ωэ2	+ ω02 )
				4λ(λ2 + ωэ2	+ ω02 )
					111

−λ

π[λ2

+ ( ω02

−λ2

−ω0 )2

][λ2 + ( ω02 −π 2 +ω0 )2 ]

8λ(λ2

+ω02 )

π[λ2

][λ2 +( ω02 +λ2 +ω0 )2 ]

+( ω02

+λ2

−ω0 )2

ω0

+λ +

8λ(λ2

+ω02 )

Более точно эквивалентную ширину спектра мощности исследуемого сигнала для колебательных моделей КФ можно определить в соответствии с выражением

∞∫Sx (ω)dω

ωэ = ωэ +	ωэ' = ωэ	+	ωэ			.	(9.33)
			Sx	(ωэ	)

С учетом определения спектральной функции формула (9.33) преобразуется к

виду:

ωэ =ωэ +	Fx (∞)− Fx (ωэ )	=ωэ	+	0,5 − Fx (ωэ )	.	(9.34)
	Sx (ωэ )
				Sx (ωэ )

В таблице 9.8 приведены аналитические выражения эквивалентной ширины спектра ωэ' для колебательных моделей КФ, полученные с использованием форму-

лы (9.33), (9.34).

Аналитические выражения для оценки эквивалентной ширины спектра Таблица 9.8

№ КФ

ωэ'

2λ 1 +

−ω

+ω

arctg

+ arctg

−

2π

ω +

Sx (ωэ )

)

ω −ω

ω +ω

λ[ln(λ2 +(ωэ −ω0 )

−ln(λ2 +(ωэ +ω0 )

)]−2ω0 arctg

+arctg

4πω0

ω +

Sx(ωэ)

λ[ln(λ2 +(ωэ −ω0 )2 )

−ln(λ2 +(ωэ +ω0 )2 )]+

−ω

+ω

2ω0 arctg

+arctg

−

4πω0

ω +

Sx (ωэ )

112

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 3111 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
25.09.20192.26 Mб8Vse_lektsii_po_assembleru.docx
#
16.03.2015131.26 Кб56Vse_otvety.docx
#
16.03.2015417.28 Кб166vse_voprosy.doc
#
09.11.2019638.46 Кб13Vvedenie_v_logiku_i_teoriyu_avtomatov.doc
#
16.03.2015280.47 Кб11VVT_KursovoyPrimer.pdf
#
16.03.20157.27 Mб12Vychislitelny_praktikum.pdf
#
16.03.201598.3 Кб12wop_int_11.doc
#
07.06.2015120.32 Кб34Word.doc
#
07.06.201574.24 Кб15XVIII век.doc
#
07.06.201540.68 Кб25ya.docx
#
07.06.2015337.57 Кб157yagudina_ot_istoria_testi.pdf