
- •Министерство образования и науки Республики Казахстан
- •1. Учебная программа дисциплины – Syllabus
- •1. 1. Данные о преподавателях:
- •1.1 Данные о дисциплине:
- •Выписка из учебного плана
- •1.5. Краткое описание дисциплины
- •1.6. Перечень и виды заданий и график их выполнения:
- •Виды заданий и сроки их выполнения
- •1.7. Список литературы
- •1.8. Контроль и оценка знаний
- •Распределение рейтинговых баллов по видам контроля
- •Календарный график сдачи всех видов контроля
- •Оценка знаний студентов
- •2. Содержание Активного раздаточного материала
- •2.1 Тематический план курса составляется в виде таблицы, где указываются наименование темы и количество академических часов, предусмотренных для каждой темы. Тематический план курса
- •2.2 Конспект лекционных занятий
- •Глава 1. Основные понятия и определения статистики
- •Тема 2. Показатели описательной статистики. Среднее, дисперсия, стандартное отклонение, эксцесс, асимметрия, интервалы. Компьютерные технологии получения дескриптивной статистики.
- •Глава 2. Выборки.
- •Тема 5. Анализ одной выборки. Анализ однородности выборки. Доверительные интервалы для среднего. Доверительные интервалы для средних выборок. Компьютерные технологии анализа.
- •Тема 6. Анализ двух выборок. Выявление достоверности различий. Параметрические и непараметрические методы анализа выборок. Компьютерные технологии анализа одной выборки.
- •Глава 3. Анализ статданных.
- •Тема 7. Дисперсионный анализ статданных. Однофакторный дисперсионный анализ статистических данных. F- тест для для дисперсий. Компьютерные технологии анализа.
- •Тема 8. Корреляционный анализ статданных. Коэффицент корреляции Пирсона. Коэффициент ранговой корреляции. Ложная и истинная корреляция Компьютерные технологии анализа.
- •Глава 4. Регрессионный анализ.
- •Тема 9. Регрессионный анализ статданных. Простая линейная регрессии. Оценивание параметров линейной регрессиии методом наименьших квадратов, коэффициент детерминации.
- •Тема 10. Оценка существенности параметров линейной регрессии. Оценка качества регрессии f-критерий Фишера, t-статистика. Проверка значимости параметров регрессии. Понятие нелинейной регрессии.
- •Тема 11. Множественная регрессия. Многомерная регрессионая модель. Фиктивные переменные. Кодирование значений качественных переменных. Мультиколлинеарность.
- •Глава 5. Анализ временных рядов.
- •Тема 12. Анализ статданных в виде временных рядов. Временные ряды и их характеристики. Аддитивная и мультипликативная модель. Декомпозиция временного ряда.
- •Тема 13. Анализ и получение тренда. Методы аналитического выравнивания. Метод скользящего среднего. Метод экспоненциального сглаживания. Оценка точности трендовой модели.
- •Тема 14. Модели временных рядов. Понятие об авторегрессионных моделях временных рядов. Коэффицент автокорреляции и автокорреляционная функция.Тест Дарбина-Уотсона.
- •Тема 15. Анализ моделей временных рядов. Решение проблемы автокорреляции. Учет сезонности. Коинтеграция временных рядов.Тест Энгла - Гренжера. Современные тенденции статанализа.
- •2.3 Планы лабораторных занятий
- •Технология построения трендов в Microsoft Excel Порядок выполнения лабораторной работы
- •Форматирование метки линии тренда.
- •Задание на выполнение лабораторной работы:
- •Задание на выполнение лабораторной работы
- •2.4 Планы занятий в рамках самостоятельной работы студентов под руководством преподаватля (срсп)
- •Тема 1. Функции распределения дискретной случайной величины. Биномиальное распределение. Применение компьютерных технологий при статистическом исследовании биномиального распределения. (2 ч.)
- •Тема 3. Функции распределения дискретной случайной величины. Распределение Пуассона. Применение компьютерных технологий при статистическом исследовании распределения Пуассона. (2 ч.)
- •Тема 4. Функции распределения непрерывной случайной величины. Гауссово распределение. Применение компьютерных технологий при статистическом исследовании Гауссово распределения. (2 ч.)
- •Тема 5. Функции распределения непрерывной случайной величины. Распределение хи-квадрат. Применение компьютерных технологий при статистическом исследовании распределения хи-квадрат. (2 ч.)
- •Тема 6. Функции распределения непрерывной случайной величины. Распределение Стьюдента. Применение компьютерных технологий при статистическом исследовании распределения Стьюдента. (2 ч.)
- •Тема 7. Функции распределения непрерывной случайной величины. Распределение Фишера. Применение компьютерных технологий при статистическом исследовании распределения Фишера. (2 ч.)
- •Тема 9. Генерация случайных чисел. Применение компьютерных технологий при генерации случайных чисел. (2 ч.)
- •Тема 10. Статистические гипотезы. Одновыборочный z-тест для средних величин. Применение компьютерных технологий при проведении одновыборочного z-теста для средних величин. (2 ч.)
- •Тема 11. Статистические гипотезы. Двухвыборочный z-тест для средних величин. Применение компьютерных технологий при проведении двухвыборочного z-теста для средних величин. (2 ч.)
- •Тема 12. Статистические гипотезы. Одновыборочный t-тест для средних величин. Применение компьютерных технологий при проведении одновыборочного t-теста для средних величин. (2 ч.)
- •Тема 15. Статистические гипотезы. Парный двухвыборочный t-тест для средних величин. Применение компьютерных технологий при проведении парного двухвыборочного t-теста для средних величин. (2 ч.)
- •2.5 Планы занятий в рамках самостоятельной работы студентов (срс)
- •Тема 1. Регрессионный анализ с применением компьютерных технологий. Интерпретация результатов.
- •Тема 2. Регрессионный анализ. Метод наименьших квадратов (мнк).Интерпретация результатов.
- •Тема 3. Регрессионный анализ. Анализ вариации зависимой переменной.
- •Тема 4. Регрессионный анализ. Условия Гаусса-Маркова по классической нормальной линейной регрессионной модели.
- •Тема 5. Регрессионный анализ. Стандартная ошибка регрессии.
- •Тема 6. Регрессионный анализ. Стандартные ошибки коэффициентов регрессии.
- •Тема 7. Регрессионный анализ. Проверка гипотез по коэффициентам регрессии.
- •Тема 8. Регрессионный анализ. Нелинейные регрессии.
- •Тема 9. Регрессионный анализ. Прогнозирование в регрессионных моделях.
- •Тема 10. Временные ряды. Анализ временных рядов с применением компьютерных технологий. Получение тренда. Интерпретация результатов.
- •Тема 11. Временные ряды. Анализ временных рядов с применением компьютерных технологий. Исследование автокорреляции данных временного ряда.
- •Тема 12. Временные ряды. Анализ временных рядов с применением компьютерных технологий. Тест Дарбина-Уотсона.
- •Тема 13. Временные ряды. Анализ временных рядов с применением компьютерных технологий. Тест на коинтеграцию на основе критерия Энгла-Грэнжера.
- •Тема 14. Статистический программный инструментарий. Обзор статистических функций ms Excel.
- •Тема 15. Статистический программный инструментарий. Обзор возможностей пакета "Анализа данных" ms Excel.
- •2.6. Тестовые задания для самоконтроля с указанием ключей правильных ответов
- •24. Имеют ли в общем случае смысловую нагрузку свободный член уравнения линейной регрессии?
- •25. Что такое корреляционные поля?
- •26. Что такое авторегрессионая модель временного ряда?
- •27. Что означает регрессионная модель с лагированными переменными?
- •28. Какой показатель определяется отношением дисперсии результативного признака регрессии к общей дисперсии результативного признака?
- •29. Какой критерий применяется для проверки гипотезы - средние двух выборок относятся к одной и той же совокупности?
- •30. Какой метод применяется для проверки гипотезы - относится та или иной вариант к данной статистической совокупности?
- •Перечень экзаменационных вопросов по пройденному курсу
- •Глоссарий
- •Выходные сведения
Тема 2. Показатели описательной статистики. Среднее, дисперсия, стандартное отклонение, эксцесс, асимметрия, интервалы. Компьютерные технологии получения дескриптивной статистики.
Показатели описательной статистики
Для того чтобы обнаружить общие свойства совокупности, выявить закономерности и в результате получить правильные выводы, необходимы обобщающие, количественные показатели. Они позволят определить тенденцию развития процесса или явления, нивелировать случайные, индивидуальные отклонения, подсчитать риск того или иного решения и, кроме того, сравнить различные вариационнные ряды (различные наборы данных). Эти количественные показатели называются показателями описательной статистики. Средний курс валют на бирже, прожиточный минимум, дифференциация доходов населения, количество денег, которое потратят потребители - все это относится к показателям описательной статистики.
Показатели описательной статистики можно условно разделить на четыре группы:
1. Показатели уровня - описывают положение данных на числовой оси. К такого рода показателям относятся минимальный и максимальный элементы выборки, верхний и нижний квартили, перцентиль, а также различные средние и другие характеристики.
2. Показатели рассеяния - описывают степень разброса данных относительно своего центра. Примерами таких показателей являются, прежде всего, дисперсия, стандартное отклонение, размах выборки, межквартильный размах и т.д.
3. Показатели асимметрии - характеризуют симметрию распределения данных около своего центра. К этой группе показателей относятся коэффициент асимметрии, эксцесс, положение медианы относительно среднего и т.д.
4. Показатели, которые описывают закон распределения данных. К ним относятся таблицы частот, кумуляты, гистограммы.
Показатели описательной статистики. Показатели уровня.
К количественным характеристикам набора данных, которые относятся к показателям уровня относятся минимальный и максимальный элементы выборки, верхний и нижний квартили, перцентиль, а также различные средние и т.д.
Виды средних величин и методы их расчета.
Среди показателей описательной статистики большое значение имеют средние, поскольку они позволяют обобщить полученные данные и охарактеризовать их с помощью типичного значения.
Средней величиной называется показатель, который характеризует обобщенное значение признака или группы признаков в исследуемой совокупности. Средняя величина заменяет большое число индивидуальных значений признака, обнаруживая общие свойства, присущие всем единицам совокупности. Это, в свою очередь, позволяет избежать случайных причин и выявить общие закономерности, обусловленные общими причинами. Используются две категории средних величин.
1. Степенные средние
2. Структурные средние
Первая категория - степенные средние - включает среднюю арифметическую, среднюю гармоническую, среднюю квадратическую и среднюю геометрическую. Вторая категория — это мода и медиана.
Средние величины, кроме того, бывают простые и взвешенные. Взвешенными средними называются величины, которые учитывают, что некоторые варианты значений признака могут иметь различную частоту, в связи с чем каждый вариант приходится умножать на эту частоту. Иными словами,"весами" выступают числа единиц совокупности в разных группах, т.е. каждый вариант "взвешивают" по своей частоте. Частоту f называют статистическим весом, или весом средней.
Средняя арифметическая - самый распространенный вид средней. Она используется, когда расчет осуществляется по несгруппированным статистическим данным, где нужно получить среднее слагаемое. Средняя арифметическая - это такое среднее значение признака, при получении которого сохраняется неизменным общий объем признака в совокупности. Формула средней арифметической (простой) имеет вид:
![]() =
=![]()
где n — численность совокупности.
Если данные сгруппированы в вариационные ряды, то расчет средней величины производится по сгруппированным данным. В этом случае речь идет об использовании взвешенной средней арифметической, которая имеет вид:
![]() =
=![]()
Среднюю гармоническую называют обратной средней геометрической. Просто средняя гармоническая используется тогда, когда весовые коэффициенты значений признака одинаковы. Её формула выглядит следующим образом.
![]() =
=![]()
Однако в статистической практике чаще используется гармоническая взвешенная формула которой имеет вид:
![]() =
=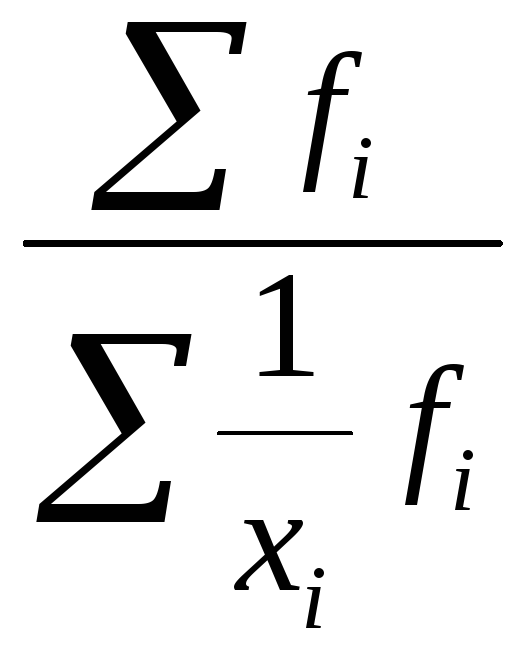
Средняя геометрическая чаще всего находит свое применение при определении средних темпов роста (средних коэффициентов роста), когда индивидуальные значения признака представлены в виде относительных величин. Она используется также, если необходимо найти среднюю между минимальным и максимальным значениями признака (например, между 100 и 100000). Формула для простой средней геометрической имеет следующий вид:
![]() =
=![]()
Медиана и мода.
Для определения структуры представленных данных используются особые средние показатели, к которым относятся медиана и мода, или так называемые структурные средние. Если средняя арифметическая рассчитывается на основе всех вариантов значений признака, то медиана и мода характеризуют величину того варианта, который занимает определенное среднее положение в ранжированном вариационном ряду.
Медиана (Me)— это величина, которая соответствует варианту, находящемуся в середине ранжированного ряда.
Для ранжированного ряда с нечетным числом индивидуальных величин (например, 1, 2, 3, 3, 6, 7, 8, 8, 10) медианой будет величина, которая, соответственно, расположена в центре ряда, т.е. пятая величина.
Для ранжированного ряда с четным числом индивидуальных величин (например, 1, 5, 7, 10, 11, 14) медианой будет средняя арифметическая величина, которая рассчитывается из двух смежным величин. Для нашего случая медиана равна (7 + 10)/2 = 8,5.
Иными словами, для нахождения медианы сначала необходимо определить ее порядковый номер (ее положение в ранжированном ряду) по формуле:
![]()
![]()
где n — число единиц в совокупности.
Численное значение медианы определяют по накопленным частотам в дискретном вариационном ряду. Для этого сначала следует указать интервал нахождения медианы в интервальном ряду распределения. Медианным называют первый интервал, где сумма накопленных частот превышает половину наблюдений от общего числа всех наблюдений.
Ранг, перцентиль и квартиль
При анализе взаимного расположения значений признака в наборе данных, наряду с такими понятиями, как медиана и мода, используются также понятия ранга, перцентиля и квартиля. Под рангом (R) понимают номер (порядковое место) значения случайной величины в наборе данных. Правила присвоения рангов состоят в следующем.
1. Если в наборе данных все числа разные, то каждому числу х, присваивается уникальный ранг R.
2. Если в наборе данных встречается группа из k одинаковых чисел хi = хi+1 = хi+2 =… хi+k, то ранг у них одинаковый и равен рангу первого числа из этой группы Ri,. Число, следующее за этой группой, получает ранг, равный Ri+k.
3. Если данные упорядочены в порядке убывания, то
а) максимальное значение в наборе данных имеет ранг, равный 1;
б) минимальное значение в наборе данных имеет наибольшее значение ранга, равное n-kmin+1 где n — количество данных в наборе, kmin - количество повторяющихся минимальных значений в наборе данных.
4. Если данные упорядочены в порядке возрастания, то
а) минимальное значение в наборе данных имеет ранг, равный 1;
б) максимальное значение в наборе данных имеет наибольшее значение ранга, равное n-kmax+1, где n - количество данных в наборе, kmax - количество повторяющихся максимальных значений в наборе данных.
Перцентиль обобщает информацию о рангах, характеризуя значение, достигаемое заданным процентом общего количества данных, после того, как данные упорядочиваются (ранжируются) по возрастанию. Перцентили - это характеристики набора данных, которые выражают ранги элементов в виде процентов от 0 до 100%, а не в виде чисел от 1 до n, таким образом, что наименьшему значению соответствует нулевой перцентиль, наибольшему - 100-й, медиане - 50-й и т.д. Перцентили можно рассматривать как показатели, разбивающие наборы количественных и порядковых данных на определенные части. Например, 70-й перцентиль эффективности продаж может быть равен 60 тыс. тенге. (измерен не в процентах, а в тенге, как и элементы набора данных). Если этот 70-й перцентиль, равный 60 тыс. тенге., характеризует деятельность определенного агента по продажам , то это означает, что приблизительно 70% других агентов имеют результаты ниже, чем у этого агента, а 30% имеют более высокие результаты.
Перцентили используются для двух целей.
1. Чтобы показать значение элемента при заданном перцентильном ранге (например,
"20-й перцентиль равен 40 тыс. тенге.").
2. Чтобы показать перцентильный ранг значения данного элемента в наборе данных (например, "эффективность продаж агента по сбыту А составляет 25 тыс. тенге., что соответствует 60-му перцентилю.
Дополняют набор базовых характеристик квартили, определяемые как 25-й и 75-й Перцентили. Ранги квартилей вычисляются по следующим формулам:
Ранг нижнего квартиля = (1 + int/{(1 + n)/2})/2
Ранг верхнего квартиля = n + 1 - pанг нижнего квартиля,
где int означает функцию взятия целого, которая отбрасывает дробную часть числа.
Такие характеристики, как наименьшее значение, нижний квартиль, медиана, верхний квартиль и наибольшее значение, дают достаточно ясное представление об особенностях набора данных. Два экстремума (наибольшее и наименьшее значение данных) характеризуют размах (диапазон) данных, медиана показывает центр, два квартиля определяют границы, которые расположены в центре каждой половины данных, а положение медианы относительно квартилей дает грубое представление о наличии или отсутствии асимметрии.
Показатели рассеяния
Степень разброса данных относительно своего центра описывают показатели рассеяния. К таким показателям относятся размах выборки, дисперсия, стандартное отклонение, межквартильный размах и т.д.
Размах выборки (Rs) - самый доступный (по простоте расчета) абсолютный показатель, который определяется как разность между самым большим и самым малым значениями признака у единиц данной выборки:
Rs = X max -X min
Размах выборки (размах колебаний) - важный показатель колебания признака, но позволяет увидеть только крайние отклонения, что ограничивает область его применения. Для более точной характеристики вариации признака на основе учета его колебаний используются другие показатели.
Среднее линейное отклонение d, которое вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности. Эта величина определяется как средняя арифметическая из абсолютных значений отклонений от средней. Все отклонения берутся по модулю.
Формула среднего линейного отклонения (простая)
![]()
Формула среднего линейного отклонения (взвешенная)
![]()
Оценки вариации
При использовании
показателей среднего линейного отклонения
возникают определенные неудобства,
связанные с тем, что приходится иметь
дело не только положительными, но и с
отрицательными величинами. Это привело
к поиску других способов оценки вариации,
чтобы иметь дело только с положительными
величинами. Таким способом стало
возведение всех отклонений во вторую
степень. Обобщающие показатели, найденные
с использованием вторых степеней
отклонений, получили широкое
распространение. К таким показателям
относятся среднее квадратическое
отклонение
![]() и среднее квадратическое отклонение в
квадрате
и среднее квадратическое отклонение в
квадрате![]() , которое называют дисперсией.
, которое называют дисперсией.
Среднее квадратическое отклонение позволяет оценить степень разброса случайных значений относительно средней величины. Для расчета среднего квадратического отклонения используется средняя квадратическая величина.
Формула простой средней квадратической

Формула для расчета взвешенной средней квадратической
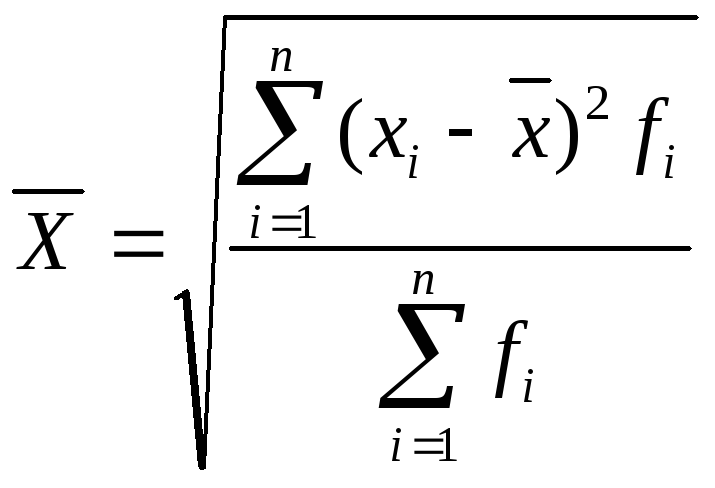
Дисперсия (![]() )
- это средний квадрат отклонений
индивидуальных значений признака от
его средней величины.
)
- это средний квадрат отклонений
индивидуальных значений признака от
его средней величины.
Формула дисперсии :
![]() .
.
Формула несмещенной дисперсии:
![]() .
.
Формула дисперсии (взвешенной):
![]() .
.
Средняя ошибка
(![]() )
характеризует стандартное отклонение
выборочного среднего, рассчитанное по
выборке размераn
из генеральной совокупности, и зависит
от дисперсии генеральной совокупности
и объема выборки n:
)
характеризует стандартное отклонение
выборочного среднего, рассчитанное по
выборке размераn
из генеральной совокупности, и зависит
от дисперсии генеральной совокупности
и объема выборки n:
![]()
![]()
Средняя ошибка
выборки
![]() используется для расчета предельной
ошибки выборки
используется для расчета предельной
ошибки выборки![]()
![]() ,
которая позволяет выяснить, в каких
пределах находится величина средней
по генеральной совокупности.
,
которая позволяет выяснить, в каких
пределах находится величина средней
по генеральной совокупности.
Установлено, что
предельная ошибка выборки
![]() связана со средней ошибкой выборки
связана со средней ошибкой выборки![]() соотношением:
соотношением:
![]() =t*
=t*![]()
где t - коэффициент доверия (определяется в зависимости от того, с какой доверительной вероятностью нужно гарантировать результаты выборочного обследования).
Кроме показателей вариации, выраженных в абсолютных величинах, в статистическом исследовании используются показатели вариации (V), выраженные в относительных величинах. Они используются для сравнения колебаний различных признаков одной и той же совокупности или для сравнения колебаний признака в нескольких совокупностях.
Данные показатели
рассчитываются как отношение размаха
вариации к средней величине признака
(![]() ,
коэффициент осцилляции), отношение
среднего линейного отклонения к
средней величине признака (
,
коэффициент осцилляции), отношение
среднего линейного отклонения к
средней величине признака (![]() ,
линейный коэффициент вариации), отношение
среднего квадратического отклонения
к средней величине признака (
,
линейный коэффициент вариации), отношение
среднего квадратического отклонения
к средней величине признака (![]() ,
коэффициент вариации) и, как правило,
выражаются в процентах.
,
коэффициент вариации) и, как правило,
выражаются в процентах.
Формулы расчета относительных показателей вариации:
![]()
![]()
![]()
Из приведенных формул видно, что чем больше коэффициент V приближен к нулю, тем меньше вариация значения признака.
На практике наиболее часто используется коэффициент вариации. Он применяется не только для сравнительной оценки вариации, но и для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному распределению).
Показатели асимметричности
При использовании показателей асимметричности можно определить форму кривой распределения и выяснить общий характер распределения, что предполагает оценку степени его однородности, а также вычисления показателей эксцесса и асимметрии.
Эксцесс (Ek
)![]() характеризует
«крутизну», т.е островершинность или
плосковершинность распределения. Он
может быть рассчитан для любых
распределений. Если эксцесс больше
0 (Ek
>0), то распределение островершинное,
если меньше 0 (Ek
<0) - то плосковершинное.
характеризует
«крутизну», т.е островершинность или
плосковершинность распределения. Он
может быть рассчитан для любых
распределений. Если эксцесс больше
0 (Ek
>0), то распределение островершинное,
если меньше 0 (Ek
<0) - то плосковершинное.
Асимметричность имеет такой показатель, как коэффициент асимметрии (As). Асимметрия, или коэффициент асимметрии, является мерой несимметричности распределения. Если этот коэффициент отчетливо отличается от 0, распределение является асимметричным. Если разбить такое распределение пополам в точке среднего (или медианы), то распределения значений с двух сторон от этой центральной точки будут неодинаковыми (те несимметричными). Такое распределение можно назвать еще "скошенным". Если As > 0, то асимметрия будет правосторонней, если As < 0 - левосторонней Если этот коэффициент близок к 0, распределение является симметричным.
Как было показано, чтобы всесторонне охарактеризовать совокупность данных, необходимо рассчитать достаточно большое количество показателей. Это можно сделать различными способами, например с помощью соответствующих функций MS Excel. Однако расчет показателей с помощью функций - сравнительно длительный процесс, MS Excel располагает инструментом Descriptive Statictics, который может быть использован для получения статистического отчета одновременно по основным показателям уровня, разброса и асимметрии выборочной совокупности.
Литература:1осн. [164-203], 5 осн. [30-37], 6 осн. [14-16], 3доп. [114-159], 4доп. [64-77], 6доп. [172-180].
Контрольные вопросы
1. Какие задачи решаются на основе анализа показателей описательной статистики?
2. На какие группы делятся описательная статистика ?
3. Каковы виды средних и методы их расчета?
4. Каковы показатели, определяющие структуру статданных?
5. Каковы показатели, определяющие взаимное расположение статданных?
Тема 3. Закономерности распределения статданных, их применение в статистическом исследовании. Нормальное распределение их, его применение в статистическом исследовании. Компьютерные технологии анализа распределения статданных.
Закономерности распределения статданных.
При исследование статданных можно заметить определенную зависимость между изменением значений варьирующего признака и частот. Частоты с увеличением значения варьирующего признака первоначально увеличиваются, а затем после достижения какой-то максимальной величины в середине ряда уменьшаются. Это свидетельствует о том, что частоты в вариационных рядах изменяются закономерно в связи с изменением варьирующего признака. Такие закономерности изменения частот в вариационных рядах называются закономерностями.
Одна из важных целей статистического изучения вариационных рядов состоит в том, чтобы выявить закономерность распределения и определить ее характер. Основной путь в выявлении закономерностей распределения состоит в построении вариационных рядов для достаточно больших по численности статистических совокупностей. Кроме того, большое значение для нахождения закономерностей распределения имеет правильное построение самого вариационного ряда. Речь идет прежде всего о таком определении оптимального числа групп и размера интервала, при котором закономерность распределения видна более отчетливо. Закономерности распределения выражают свойства явлений, общие условия, влияющие на формирование вариации признака. Когда мы говорим о характере, типе закономерностей распределения, то имеем в виду отражение в них общих условий, определяющих распределение. При этом следует учитывать, что речь идет о распределениях, отражающих однородные явления. Многие явления, рассматриваемые каждое в отдельности, изолированно друг от друга, кажутся случайными. Однако если анализировать эти явления в совокупности с другими, аналогичными по своей сущности, то часто удается обнаружить закономерность, связанную с их возникновением. Если на практике часто встречается один и тот же тип распределения частот, целесообразно описать его с помощью математической формулы, которая может служить для сравнения и обобщения различных совокупностей аналогичных данных. В статистике широко используются различные виды теоретических распределений - нормальное распределение, биномиальное распределение, распределение Пуассона и др. Каждое из теоретических распределений имеет специфику и свою область применения в различных отраслях знания.
Нормальный закон распределения
Большинство экспериментальных исследований в биологии, медицине, технике и других областях связаны с измерениями, результаты которых могут принимать практически любые значения в заданном интервале и описываются моделью непрерывных случайных величин. Одним из важнейших непрерывных распределений является нормальное, или гауссово распределение.
Нормальное распределение получило широкое распространение для приближенного описания многих случайных явлений, в которых на результат воздействует большое количество независимых случайных факторов, среди которых нет сильно выделяющихся. Кроме того, многие распределения, связанные со случайной выборкой, при увеличении ее объема переходят в нормальное. Однако следует отметить, что в природе встречаются экспериментальные распределения, для описания которых модель нормального распределения малопригодна.
Плотность вероятностей нормально распределенной случайной величины задается формулой:
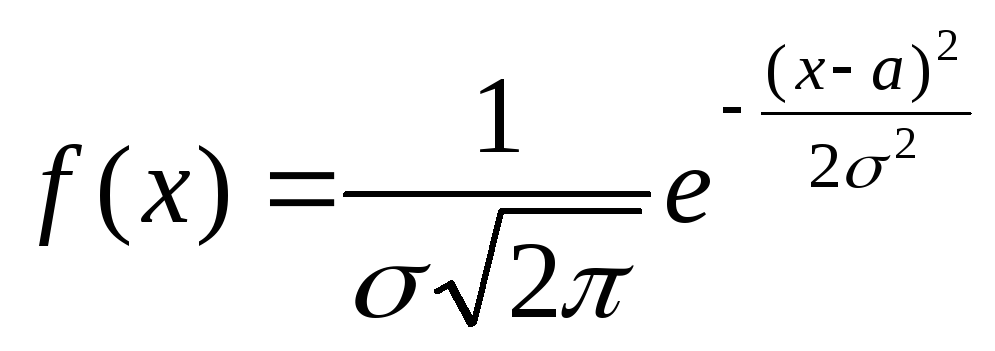 -∞<x<+∞.
(*)
-∞<x<+∞.
(*)
Таким образом, нормальное распределение определяется двумя параметрами: а и σ.
Здесь а и σ - параметры распределения. Иногда используют краткое обозначени N(a, σ2). Математическое ожидание и дисперсия случайной величины, распределенной как N(a, σ2), равны соответственно a и σ2.
Можно сказать, что нормальное распределение это совокупность объектов, в которой крайние значения некоторого признака - наименьшее и наибольшее - появляются редко; чем ближе значение признака к математическому ожиданию, тем чаще оно встречается. Например, распределение студентов по их весу приближается к нормальному распределению.
f(x)
x
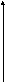
Кривая плотности нормального распределения.
Диаграмма нормального распределения симметрична относительно точки а, то есть положительные и отрицательные равновеликие отклонения от центра распределения (математического ожидания) встречаются одинаково часто. Поэтому медиана нормального распределения равна а.
Параметр σ характеризует степень сжатия или растяжения (плотности) диаграммы. Чем больше σ, тем «шире» кривая, а ее максимальная высота ниже. Кривая как бы растягивается в стороны.
В область от а - σ до а + σ нормально распределенная случайная величина попадает с вероятностью 0,683. В пределы от -2σ до +2σ случайная величина попадает с вероятностью 0,955, а в пределы от -3σ до +3σ — с вероятностью 0,997. Последняя закономерность трактуется как правило трех сигм.
Формула (*) описывает целое семейство нормальных кривых, зависящих, как было сказано ранее, от двух параметров - а и σ, которые могут принимать любые значения, поэтому существует бесконечно много нормально распределенных совокупностей.
Особую роль играет нормальное распределение с параметрами а = 0 и σ =1,то есть распределение N(0,1), которое часто называют стандартным или нормированным нормальным распределением. Плотность стандартного нормального распределения вычисляют по формуле:
![]()
![]()
Проверка соответствия теоретическому распределению. Важной задачей, возникающей при анализе, статданных является оценка меры соответствия (расхождения) полученных эмпирических данных и каких-либо теоретических распределений. Это связано с тем, что в большинстве случаев при решении реальных задач закон распределения и его параметры неизвестны. В то же время применяемые статистические методы в качестве предпосылок часто требуют определенного закона распределения.
Наиболее часто проверяется предположение о нормальном распределении генеральной совокупности, поскольку большинство статистических процедур ориентировано на выборки, полученные из нормально распределенной генеральной совокупности.
Для оценки соответствия имеющихся экспериментальных данных нормальному закону распределения обычно используют графический метод, выборочные параметры формы распределения и критерии согласия. Графический метод позволяет давать ориентировочную оценку расхождения или совпадений распределений .
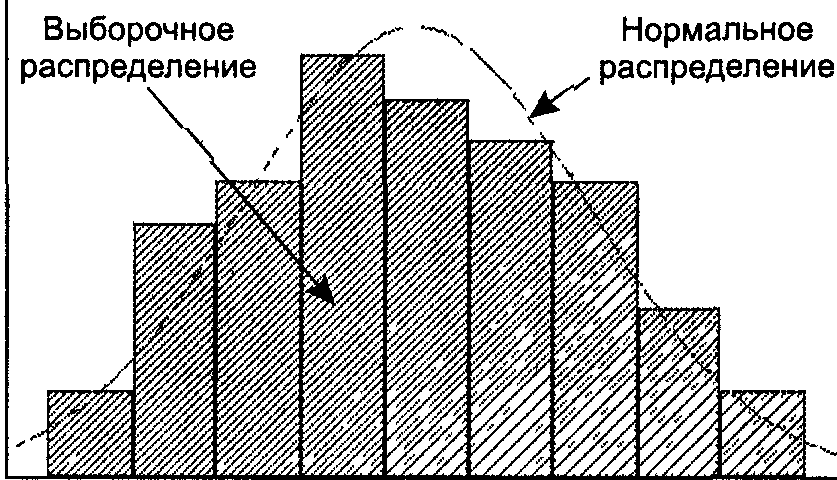
Сопоставление выборочного распределения и кривой нормального распределенния
При большом числе наблюдений (п > 100) неплохие результаты дает вычисление выборочных параметров формы распределения: эксцесса и асимметрии . Принято говорить, что предположение о нормальности распределения не противоречит имеющимся данным, если асимметрия близка к нулю, то есть лежит в диапазоне от -0,2 до 0,2, а эксцесс - от 2 до 4. Наиболее убедительные результаты дает использование критериев согласия. Критериями согласия называют статистические критерии, предназначенные для проверки согласия опытных данных и теоретической модели. Здесь нулевая гипотеза Н0 представляет собой утверждение о том, что распределение генеральной совокупности, из которой получена выборка, не отличается от нормального. Среди критериев согласия большое распространение получил непараметрический критерий X2 (хи-квадрат). Он основан на сравнении эмпирических частот интервалов группировки с теоретическими (ожидаемыми) частотами, рассчитанными па формулам нормального распределения.
Отметим, что сколько-нибудь уверенно о нормальности закона распределения можно судить, если имеется не менее 50 результатов наблюдений. В случаях меньшего числа данных можно говорить только о том, что данные не противоречат нормальному закону, и в этом случае обычно используют графические методы оценки соответствия. При большем числе наблюдений целесообразно совместное использование графических и статистических (например, тест хи-квадрат или аналогичные) методов оценки, естественно дополняющих друг друга.
Использование критерия согласия хи-квадрат. Для применения критерия желательно, чтобы объем выборки п > 40, выборочные данные были сгруппированы в интервальный ряд с числом интервалов не менее 7, а в каждом интервале находилось не менее 5 наблюдений (частот).
Отметим, что сравниваться должны именно абсолютные частоты, а не относительные (частости). При этом, как и любой другой статистический критерий, критерий хи-квадрат не доказывает справедливость нулевой гипотезы (соответствие эмпирического распределения нормальному), а лишь может позволить ее отвергнуть с определенной вероятностью (уровнем значимости).
Как было отмечено, используются и другие распределения, например, Бернулли, Пуассона, дискретное, F-распределение, t-распределение, биномиальное. C помощью статистических функций, которыми располагает Microsoft Excel, можно рассчитать вероятность случайной величины, распределенной по одному из указанных выше законов распределения. Например, есть возможность генерировать последовательность случайных чисел, распределенных по одному из перечисленных выше законов распределения, также производить оценку выборку на принадлежность к тому или иному распределению.
Литература:
1осн. [197-211], 5осн. [30-37], 3доп. [182-190], 4 доп. [78-94], 6доп. [185-188].
Контрольные вопросы
1. Для чего необходимо знать вид распределения статданных при их анализе?
2. Почему нормальное распределение широко используется в статанализе?
3. Какие теоретические распеределения, кроме нормального, используются при анализе статданных?
4. Какие параметры влияют на форму нормально распределенных статданных?
5. Каков смысл правила "трех сигм"?
