Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Байкальский государственный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математика в экономике, сборник задач

.pdf

Скачиваний:

Добавлен:

08.03.2015

Размер:

1.91 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 2015 16 17 18 19 20 > Следующая >>>

5.17. Используя метод интегрирования по частям, вычислить интегра-

лы:

	π									e
1)	ò xsin xdx;								2)	ò xln xdx ;
	0									1
										e
		3								e	(1+ ln x)2 dx ;
3)	òarctgxdx ;								4)	ò	(1+ ln x)2 dx ;
	0									1
	π			xdx						1	arcsin x
	3			xdx						1	arcsin x				dx ;
5)	ò							;	6)	ò
					2		x
			cos		2								1+ x
	π		cos							0			1+ x
	6									π
	e			ln x		dx ;				π
7)	ò									4		2
										4
									8)	ò x			cos2xdx			;
	1	e							8)	ò x			cos2xdx			;
		e								0
	π									0
	π										π 2
9)	ò2 e2 x				cos xdx ;				10)		ò4 sin
9)	ò2 e2 x				cos xdx ;				10)		ò4 sin			xdx ;
	0										0

5.18. Найти среднее значение функции на указанном отрезке:

а) f (x) = cos2 x, 0 £ x £ π;			б) f (x) =			1	, 0	£ x £ 1;

						- x2
	π		4			- x2
в) f (x)= tg2 x, 0 £ x £		;	г) f (x)=		, 0 £ x £ 1;
в) f (x)= tg2 x, 0 £ x £		;	г) f (x)=	x	, 0 £ x £ 1;
д) f (x)= 1 ,1£ x £ 2.	4
д) f (x)= 1 ,1£ x £ 2.
x

5.19. Определить дневную выработку Q рабочего за семичасовой рабо- чий день, если производительность труда u (у. ед./ч) в течение дня описывает- ся функцией u = u0 ×(- 0,025t2 + 0,2t + 0,6), где t − время в часах от начала сме- ны, u0 − производительность в начале смены.

5.20.Функция y = 5t + 3t2 (у. ед./ч) определяет интенсивность поступ- ления продукции на склад в любой момент времени t, отсчитываемый в часах от начала поступления продукции на склад. Определить количество продук- ции, поступившей на склад за первые три часа приёма.

5.21.Зависимость нагрузки на трансформаторную подстанцию (в кило- ваттах) от времени суток (в часах от начала суток) выражается формулой

é π	æ t	öù	, здесь a, b − параметры. Определить: 1) расход элек-
y = a + b ×cosê	ç	+ 3÷ú

ë12	è 2	øû

троэнергии потребителями за сутки (за время от 0 до 24 часов); 2) провести расчёт при следующих числовых значениях параметров: a = 25 тыс. квт., b = 15 тыс. квт.

141

5.22. Мощность y потребляемой городом электроэнергии выражается

формулой
ìa,			0 £t < 6;
ï		π
y = í		π	(t - 6), 6
ïa + b×sin				£ t £ 24,
ïa + b×sin	18			£ t £ 24,
î	18

где t (ч) − текущее время суток, a, b − постоянные. Найти суточное потребле- ние электроэнергии: 1) при любых значениях a и b; 2) при a =15000 квт ,

b= 12000 квт.

5.23.Определить суммарные издержки производства за прошедший

период, если объём производства изменялся в пределах 3 ≤ q ≤ 27, предель- ные издержки определялись равенством MC(q) = 3q .

5.24. Найти средний прирост издержек, если объём продукции q изме- няется от q1 до q2 единиц, а предельные издержки зависят от объёма произ-

ведённой продукции:

MC = f (q).

Указать объём продукции

из отрезка

[q1;q2 ],

при котором издержки принимают среднее значение.

Решить задачу

для случаев, когда:

MC = 3q2 +4q +1, [q ;q

] = [0;3];

2) MC = 6q2 + 4 , [q ;q

] = [1;4]

5.25. По заданным чистым инвестициям I (t) = 60003

(тыс. руб./год):

вычислить приращение капитала за восемь лет, начиная с

t1 = 0; 2) опре-

делить,

за сколько лет приращение капитала составит 63 000

(тыс. руб.).

(Напомним, чистыми называют инвестиции, идущие на прирост капитала).

5.3. Интеграл с переменным верхним пределом. Восстановление функции по её производной

Если

f (x)− непрерывная на

отрезке

[a,b] функция, то x [a,b] суще-

æ x

ö′

′

ствует производная

= f (x). Если

(F(x)) = f (x)

и известно значение

ç ò

f (t)dt ÷

èa

функции F(a), тогда x [a,b] верна формула

F(x)= F(a)+ òx

f (t)dt .

5.26.

Найти:

а)

òsin x

dx;

б)

òsin x

dx;

в)

òsin x

dx .

dx a

da a

db a

5.27. Найти производные следующих функций:

142

y =

2sin t dt ;

y =

2 x

y = òcost2dt ;

2sin t2dt ;

y = ò

1+ t4 dt ;

x = ò 3

ln zdz ;

y = ò z2 ln zdz .

5.28. Найти пределы:

	x			x2
1) lim	òcos2 tdt	;		òsin	xdx
	0		2) lim	0		;
	x			0
				x3
x→0			x→0	x3

5.29. Найти точки экстремума функций:

	æ x	2			ö2
	çòet			dt ÷
3) lim	è 0				ø	.
3) lim	x					.
x→∞	òe2t		2		dt
	òe2t				dt
	0

x	2					x		t2
1) y = ò t			- 5t +t		4dt ;	2) y = òe	−		(1- t2 )dt ;
1) y = ò t			- 5t +t		4dt ;	2) y = òe	−	2	(1- t2 )dt ;
0		2 + e				1
	x		sin t
3)* y = ò				dt	в области	x > 0 .
3)* y = ò			t	dt	в области	x > 0 .
	0		t

5.30. Известна функция MC = f (Q), описывающая зависимость пре- дельных издержек фирмы MC от объёма выпущенной продукции Q. Опре- делить функцию полных (или суммарных) издержек фирмы при условии, что

постоянные издержки фирмы равны								С0 д. ед. Решить задачу:
	1) в общем виде;							= 90 ;
	2) при MC = Q2 + 3Q + 5, C0
	3) MC =				6	,	С0 = 2 ; определить суммарные издержки производства
			1		+ 3Q

за прошедший период, если 0 £ Q £ 27;
	4) MC = 22 -8×Q + 3×Q2 + 2 ×Q3 , С0 = 55;								рассчитать	общие затраты
при выпуске 3 первых единиц продукции.
	5.31. Кривая						предельных	издержек	задаётся	уравнением
MC =	1			,	q ³ 0		. Определить: а) кривую полных издержек, если извест-
		(1 + 5q)2
но,		что						C(0) = 2	тыс.	руб.;

б) прирост суммарных и средний прирост суммарных издержек, если извест- но, что 2 £ q £ 7 .

5.32. Определить зависимость суммарного дохода R = R(Q) предпри- ятия от объёма реализованной продукции Q , если известен предельный до- ход MR = f (Q). Решить задачу:

143

1) в общем виде;

2) при MR = 9Q − 6 ;

3) при MR =

+ 5Q3 .

Q +1

5.33.

Определить зависимость потребления C от национального дохода

Y , если

предельная склонность к

потреблению

задаётся формулой

MC = 0,5 +

. Кроме того известно,

что потребление составляет 85 (у.

10 Y

ед.), когда национальный доход равен 100 (у. ед.).

5.34.

По заданным чистым инвестициям I (t)= 70×

спрогнозиро-

3t +1

вать динамику основного капитала во времени, если в начальный момент времени t = 0 основной капитал составлял 1000 д. ед.

5.4. Некоторые геометрические приложения определённого интеграла

1. Вычисление площадей плоских фигур. Вычисление площади лю-

бой плоской фигуры следует свести к вычислению суммы или разности пло-

щадей криволинейных трапеций и далее воспользоваться геометрическим смыслом определённого интеграла.

5.35. Вычислить площади фигур, ограниченных линиями:

1) x = 0, x = 2 , y = 2x , y = 2x - x2 ;	2)		y = 4 - x2 , y = 0;
3) y = ln x , x = e , x =1;	4) y = x2 , y = 2 - x2 ;
5) y = x2 , x + y − 2 = 0;	6)	x = -2 y2 , x = 1- 3y2 ;
7) y2 = 4x , 4y = x2 ;	8)		y = 4x2 , y = x2 9 , y = 4;
9) y = cos2 x - sin2 x , y = 0, x = 0, x = π 4 ;	10)		y = sin x , y = x2 -π × x ;

11) xy = 6 ,	y = 7 − x ;			12) y =	x	+1,	y = 0,	x = −2 , x = 1.

5.36.	Найти	площадь	фигуры,	заключённой			между	параболой
y = x2 - 2x + 2 , касательной к ней в точке				(3;5) и осью ординат.
5.37.	Найти	площадь	фигуры,	заключённой			между	параболой
y = -x2 + 4x - 3 и касательными к ней в точках (0;−3) и(3;0).

144

2.Решение некоторых экономических задач.

∙Кривая Лоренца устанавливает за-

висимость процента доходов от процента имеющих их населения. При равномерном

распределении доходов кривая Лоренца вырождается в биссектрису ОА (см. рис. 5.2), в противном случае кривая Лоренца

представляет из себя некоторую кривую ОВА. Коэффициентом Джини или коэффи- циентом концентрации называется показа-

	тель G , который равен отношению площа-
	ди замкнутой фигуры ОАВ к площади тре-
	угольника ОАС, 0 ≤ G ≤ 1. Коэффициент
	Джини характеризует степень неравенства
	в
распределении	доходов населения: чем больше коэффициент, тем менее

равномерно распределены доходы.

∙ Излишек (избыток, выигрыш, рента) потребителя - это разница меж-

ду максимальной суммой, которую потребитель готов уплатить за данное ко- личество товара и его фактическими затратами на приобретение, иначе - вы- игрыш потребителя при покупке, обусловленный превышением полезности приобретаемых единиц товара над его ценой (напомним, что кривая спроса совпадает с кривой предельной полезности товара).

Рассмотрим кривую индивидуального спроса некоторого товара, за- данную уравнением P = f (Q) и изображённую на рис. 5.3 . Если покупатель приобрёл товар по цене P0 в количестве Q0 то излишек потребителя соста-

вил величину, численно равную площади заштрихованной на рисунке фигу- ры. В описанной ситуации потребитель действовал рационально: приобрёл товар в таком количестве, что предельная полезность последней купленной единицы, выраженная в денежной форме, равна цене товара.

145

Излишек (рента, выигрыш) производителя (предпринимателя, продав-

ца) - это разница между суммой, за которую производитель реализовал товар и минимальной суммой, за которую он был готов продать этот товар. Рас- смотрим кривую индивидуального предложения некоторого товара, заданную

уравнением	P = g(Q)	и изображённую на рис. 5.4. Если производитель реа-
лизует товар по цене		P0 в количестве Q0 , то излишек продавца составит ве-
личину, численно равную площади заштрихованной на рисунке фигуры.
		Аналогично определяются суммарные
		излишки потребителей и производителей:
		для них используются функции совокупного
		спроса и потребления на рынке рассматри-
		ваемого товара. Если на рынке товара уста-
		новилось равновесие (см. рис.5.5), то сум-
		марный излишек (рента) покупателей равен
		площади фигуры P P*E , а продавцов −
		0
		площади фигуры AP0 E .
5.38.	Найти коэффициент Джини, если кривая Лоренца задается одним
из следующих уравнений:
1) y = x3 ;		2) y = 2x -1;
5.39.	Пусть P = f (Q)− уравнение кривой спроса данного потребителя.

Определить излишек потребителя, если он приобрёл Q0 ед. товара по цене P0 = f (Q0 ). Решить задачу для следующих вариантов кривой спроса и объёма

покупок:
1) P = 1000×(0,5)Q , Q = 6;	2) P = 80 -		, Q		= 64 .
1) P = 1000×(0,5)Q , Q = 6;	2) P = 80 -	Q	, Q	0	= 64 .
0				0
5.40. Пусть P = g(Q)−	уравнение кривой предложения данного про-

давца. Определить излишек продавца, если известно, что ему удалось реали- зовать Q0 ед. товара по цене P0 = g(Q0 ). Решить задачу для следующих ва-

риантов функции предложения и объёма продаж:

1) P = 1 ×3Q	, Q0 = 4;				2) P = (Q +1)2 , Q = 8.
2				0
5.41.	Функции		цены	спроса и предложения заданы соответственно
формулами	P =	200	, P =	1	(Q2 + 2Q +1).

	d	Q +1	s	5

1)Предполагая свободную конкуренцию на рынке, определить ренты (суммарные) потребителей W и продавцов V.

2)Пусть рынок стал более либеральным за счёт внедрения на него но- вых продавцов. Функция цены спроса осталась прежней, а функция предло-

146

жения приняла вид: Ps = 21625 (Q2 + 2Q +1). Определить: каким образом при

этом изменились ренты потребителей и продавцов.

3) Пусть структура рынка полностью изменилась: он стал полностью монополизирован. Монополист установил цену на рынке Pd = 25 д. ед., а

функция цены спроса осталась прежней. Как новая ситуация повлияла на по- требительскую ренту?

5.5.Несобственные интегралы

1.Интегралы с бесконечными пределами интегрирования. Пусть функция f (x) определена на промежутке [a, + ∞) и интегрируема на любом

отрезке [a,b], a < b . Предел						lim	bò f (x)× dx называют несобственным интегра-
						b→+∞ a
лом от функции	f (x)		на промежутке [a, + ∞) и обозначают +ò∞f (x)× dx. Таким
образом, +ò∞f (x)× dx = lim								a
образом, +ò∞f (x)× dx = lim					bò f (x)× dx.
a		b→+∞ a
Если предел существует, то несобственный интеграл называют сходя-
щимся, а функцию		f (x)			− интегрируемой на промежутке [a,				+ ∞). В против-
ном случае интеграл называют расходящимся.
Аналогично определяют
bò f (x)× dx =	lim		bò f (x)× dx ,
−∞	a→ −∞ a
+ò∞f (x)× dx =	lim		òc	f (x)× dx + lim				bò f (x)× dx Þ
−∞	a→ −∞ a					b→+∞ c
+ò∞f (x)× dx =	òc	f (x)× dx +				+ò∞f (x)× dx .			(5.1)
−∞	−∞					c

где с −любое число. Интеграл +ò∞f (x)× dx сходится тогда и только тогда, когда

−∞

сходятся оба интеграла, стоящие в правой части формулы (5.1).

5.42. Вычислить несобственные интегралы или доказать их расходи- мость:

+ ∞	0	+ ∞	dx
1) òe−2 x × dx ;	2) òcos x ×dx ;	3) ò				;
			x ×ln	3	x
0	−∞	e

147

+∞

10) ò

+∞

4) ò

−∞

+ ¥

7) ò

1+ x2 ;

x ×dx ; x2 + 4

1+(2 × x )×dx ; x2 × 1+ x

	0
5)	ò x × ex × dx ;
	−∞			dx
	+¥
8)	ò
8)	ò	x	2	+ 6× x	+11
	-¥	x		+ 6× x	+11

+∞ dx

11)ò xα , где α − параметр;1

	+∞		dx
6)	ò				;

		x ×		ln x
	e	x ×		ln x
	+ ¥
9)	ò x ×cos x ×dx;
	0

+∞ x2 +1

12) ò x3 ×dx .

+∞	+∞	+∞
5.43. Вычислить интегралы ò f (x)× dx;	ò x × f (x)× dx	и ò x2 × f (x)× dx , в
−∞	−∞	−∞

которых функция f (x)− плотность вероятности случайной величины X , за- данная следующим образом:

ì0,

x < 2,

ì1

x ö

ç1-

÷, x Î(0; 4],

f (x)= í24

, x

³ 2;

2) f (x)= í2

4 ø

ï0,

x Ï(0; 4];

î x

x Î[a; b],

f (x)= íï

(равномерное распределение на отрезке

[a;b]), здесь

b - a

ï0,

x Ï[a; b],

a,b − параметры;

f (x)= íìλ ×e-λ×x , x ³ 0, (экспоненциальное (показательное) распределение с па-

î 0,

x < 0,

раметром λ > 0).

2. Интегралы от неограниченных функций. Пусть функция

f (x) оп-

ределена на промежутке

[a,b) и интегрируема на любом отрезке

[a,b − ε ],

0 < ε < b − a и не ограничена на отрезке [b − ε , b ], тогда полагают

bò f (x)×dx =

lim b−òεf (x)× dx .

ε →+0 a

Если предел существует, то несобственный интеграл называют сходя-

щимся, в противном случае интеграл называют расходящимся.

Аналогично, если f (x) определена на промежутке (a,b] и интегрируема

на любом отрезке [a + ε ,b],

0 < ε < b − a не ограничена на отрезке[a,a + ε ], то

bò f (x)× dx =

lim

bò f (x)× dx .

ε → + 0 a+ε

Если функция не ограничена в окрестности точки c (a, b), то

bò f (x)× dx =

lim

с −òεf (x)× dx + lim

bò f (x)× dx

ε → + 0 a

ε → + 0 с+ε

148

(в предположении, что f (x) интегрируема на отрезках [a,c − ε ], [c + ε ,b] при

0< ε < min{c − a,b − c})

5.44.Вычислить несобственные интегралы или доказать их расходи-

мость:

	1		dx						1			dx						2		x ×dx
1) ò						;		2)	ò						;	3)		ò								;
																			(x				4 5
										x	2		+ x	4						2	-
											2			4						2
	0	1- x							0									−2					1)
	e		dx						2			dx						1	x3	+		3			- 2
	e		dx						2			dx						1	x3	+		3		x	- 2
4)	ò						;	5)	ò						;	6)		ò									dx ;
		x ×ln		3	x									2
				3										2									x3
	1								0	(x -1)								0			5		x3
	e								1	dx
7)	òln x × dx ;							8)	ò				, где			α −параметр.
7)	òln x × dx ;							8)	ò	xα			, где			α −параметр.
	0		5.45. Для функций:						0	xα
			5.45. Для функций:															a
																ì		a			,		x Î[-1;1],
	f (x)= íìa × x,							x Î(0; 2],								2) f (x)= íï

1)																	1- x2
					0,			x Ï(0; 2];								ï							x Ï[-1;1];
					î											î0,							x Ï[-1;1];

	a		ì	−x2 2	,	x > 0,
3) f (x)=	a	;	4) f (x)= íïa × x ×e		,	x > 0,
3) f (x)=	ex + e−x	;	4) f (x)= íïa × x ×e			x £ 0.
	ex + e−x		ï0,			x £ 0.
			î

+∞

найти значения параметра a из условия ò f (x)×dx =1

−∞

149

ОТВЕТЫ

ГЛАВА 1

1.1. 1) A = {0;1; 4 };	2)	A = { 1;2;3;4 }; 3) A = Æ; 4)					A = {− 2; −1;0;1;2 };
5) A = { 1;2;3}; 6) A =	ì π	;π ;	3π	;2π	ü .	1.2. A = Æ,	A = {a },	A = {b },
	í
		2			ý	1	2	3
	î 2				þ


A4 = {c },	A5 = {a, b },		A6 = {a, c }, A7 = {b, c }, A8 = {a, b,c }; 2) B1 = Æ,
B2 = {1},	B3 = {{2,6}},		B4 = {2 }, B5 = {1, {2,6}}, B6 = {1, 2 },		B7 = {{2,6}, 2	},
B8 = {1,{2,6},2 }.		1.3. A = B = { 1;2;3;4 }.		1.4.1) AU B =	= { - 5;- 3;4	},
A I B = { 4 },			A / B = { - 5 },		B / A = { - 3};

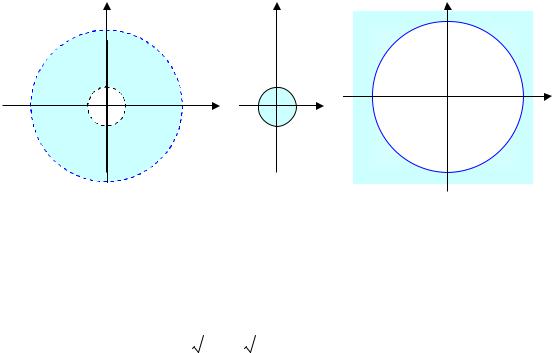
2) A U B = {(x, y)|x Î R, y Î R}, A I B = {(x, y) |1 < x2 + y2 < 4 }, см. рис.1.1,

y	y	y

1	2	x	1	x	2	x

Рис. 1.1. A I B

Рис. 1.2. A/ B

Рис.1.3. B / A

A/ B = {(x, y) | x2 + y2 £1}, см. рис.1.2,

B / A = {(x, y) | x2 + y2

³ 4 }, см. рис.1.3;

3) A U B = (3;9],

A I B = [7;8),

A / B = [8;9],

B / A = (3;7).

1.5. 1){-1;0}; 2) {1±

5;1± 3}; 3) {-

1}. 1.6.1)

ç - ¥;-

÷ ;

ê0;

ú .


1.8. 1) Z ,{-1;0;1}; 2)		{n Î N :n ¹ 3k, k Î N}, Æ;			3) (0;1];	{}1 .
1.11. 1) множество X ограничено, множество верхних граней: [1; + ¥) , мно-
жество нижних	граней:	(- ¥; -1],	sup X = 1, inf X = −1, max X = 1,
min X = −1; 2)	множество X ограничено,			множество	верхних	граней:
[3, + ¥), множество нижних граней: (- ¥;- 4],				sup X = 3,	inf X = −4,	max X

150

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 2015 16 17 18 19 20 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
11.07.2019113.15 Кб3Маркетинговые исследования Лекции.doc
#
09.11.20182.12 Mб3Маркетинговые коммуникации Гл16 КСО.doc
#
09.11.201810.26 Mб5Маркетинговые коммуникации Гл17 Соц. отчет.doc
#
11.07.2019253.44 Кб7Маркетинговые коммуникации Лекции.doc
#
09.11.2018220.16 Кб1Маркетинговые коммуникации Ответы на экзамен.doc
#
08.03.20151.91 Mб49Математика в экономике, сборник задач.pdf
#
08.03.20154.35 Mб38МатыскинаТеория статистики.pdf
#
08.03.2015207.36 Кб13Машинотех продук готовая.doc
#
08.03.2015858.47 Кб135Международное частное право.pdf
#
08.03.2015203.18 Кб9Менеджмент переделка (Восстановлен).docx
#
08.03.2015101.89 Кб12Метод указ по практике.doc