
- •2. Ускорение при плоском криволинейном движении. Нормальное и тангенсальное ускорения.
- •3. Кинематика вращения твёрдого тела вокруг закреплённой оси. Угол поворота. Угловая скорость. Угловое ускорение. Связь между линейной и угловой скоростью. Равноускоренное движение.
- •4. Законы Ньютона. Принцип относительности Галилея.
- •5. Упругие силы. Силы трения.
- •6. Закон всемирного тяготения. Сила тяжести. Вес тела. Состояние невесомости.
- •7. Импульс. Импульс силы. Закон сохранения импульса. Центр масс.
- •8. Механическая работа. Мощность. Энергия. Кинетическая энергия.
- •9. Поле сил. Консервативные силы. Потенциальная энергия. Связь между потенциальной энергией и силой.
- •10. Закон сохранения полной механической энергии частицы.
- •11. Закон сохранения энергии для системы невзаимодействующих частиц.
- •12. Взаимная потенциальная энергия частиц. Закон сохранения энергии системы частиц.
- •13. Энергия упругой деформации. Условия равновесия механической системы.
- •14. Момент импульса. Момент силы. Потенциальная энергия. Связь между потенциальной энергией и силой.
- •15. Вращение твёрдого тела вокруг закреплённой оси. Основное уравнение динамики вращательного движения твёрдого тела.
- •16. Момент инерции. Вычисление моментов инерции ноторых тел относительно оси симметрии (тонкий стержень, обруч, диск). Теорема Штейнера.
- •17. Момент инерции однородного тела вращения. Моменты инерции конуса, шара.
- •18. Кинетическая энергия вращающегося твёрдого тела вокруг закреплённой оси. Кинетическая энергия твёрдого тела при плоском движении.
- •19. Уравнения динамики твёрдого тела. Центр тяжести. Условия равновесия твёрдого тела.
- •20. Колебательное движение. Кинематика и динамика гармонических колебаний.
- •21. Кинетическая и потенциальная энергия гармонического колебания. Полная энергия гармонического колебания. Средние за период значения кинетической и потенциальной энергии.
- •22. Математический и физический маятники. Приведённая длина физического маятника. Центр качаний.
- •23. Сложение гармонических колебаний одного направления. Сложение взаимно перпендикулярных колебаний.
- •24. Затухающие колебания. Логарифмический декремент затухания. Добротность колебательной системы.
- •25. Вынужденные колебания. Явление резонанса. Резонансные кривые.
- •26. Основные понятия и исходные положения положения термодинамики. Обратимые и необратимые процессы. Круговые процессы (циклы).
- •27. Внутренняя энергия. Работа и теплота. Первое начало термодинамики.
- •28. Теплоёмкость. Молярная и удельная теплоёмкости. Связь между ними. Формула Майера.
- •29. Уравнение состояния идеального газа. Изотермический, изохорический и изобарический процессы и их уравнения. Графики этих процессов.
- •30. Адиабатический процесс. Уравнение Пуассона. Показатель адиабаты.
- •31. Политропические процессы. Уравнение политропы идеального газа. Показатель политропы.
- •32. Тепловые двигатели. К.П.Д. Теплового двигателя. Холодильный коэффицент. Различные формулировки второго начала термодинамики.
- •33. Цикл Карно. Первая теорема Карно. Вторая теорема Карно.
- •34. Рабочий цикл четырёхтактного двигателя внутреннего сгорания. К.П.Д. Цикла.
- •35. Рабочий цикл четырёхтактного двигателя внутреннего сгорания Дизеля. К.П.Д. Цикла.
- •36. Неравенство Клаузиуса. Равенство Клаузиуса. Энтропия. Изэнтропический процесс. Теорема Нернста(третье начало термодинамики).
- •37. Закон возрастания энтропии. Основное уравнение термодинамики.
- •38. Число степеней свободы механической системы. Поступательные, вращательные и колебательные степени свободы молекулы. Теорема о равнораспределении энергии по степеням свободы.
- •39. Классическая теория теплоёмкости идеальных газов.
- •40. Классическая теория теплоёмкости твёрдых тел (кристаллов). Закон Дюлонга и Пти.
- •41. Пространство скоростей. Функция распределения молекул по скоростям. Распределение Максвелла.
- •42. Распределение молекул по абсолютным значениям скоростей. Характерные скорости (наиболее вероятная, средняя, среднеквадратичная) в распределении Максвелла.
- •43. Барометрическая формула. Распределение Больцмана. Распределение Максвелла - Больцмана.
- •44. Энтропия и вероятность. Формула Больцмана. Макро- и микросостояния. Термодинамическая вероятность макросостояния (статистический вес).
16. Момент инерции. Вычисление моментов инерции ноторых тел относительно оси симметрии (тонкий стержень, обруч, диск). Теорема Штейнера.
Момент инерции — скалярная физическая величина, характеризующая распределение масс в теле, равная сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения СИ: кг·м².
Обозначение: I или J.
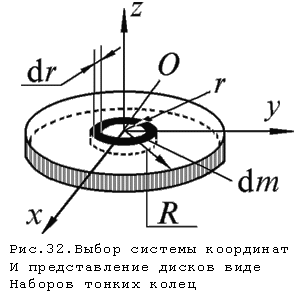 Для
расчета моментов
инерции
тонкого диска
массы m
и радиуса R
выберем систему координат так, чтобы
ее оси совпадали с главными центральными
осями (рис.32). Определим момент инерции
тонкого однородного диска относительно
оси z
, перпендикулярной к плоскости диска.
Рассмотрим бесконечно тонкое кольцо с
внутренним
Для
расчета моментов
инерции
тонкого диска
массы m
и радиуса R
выберем систему координат так, чтобы
ее оси совпадали с главными центральными
осями (рис.32). Определим момент инерции
тонкого однородного диска относительно
оси z
, перпендикулярной к плоскости диска.
Рассмотрим бесконечно тонкое кольцо с
внутренним
радиусом
r
и наружным r+dr.
Площадь такого кольца ds=2r
$\pi$ dr, а его
масса
![]() ,
гдеS= $\pi$ R2
- площадь всего диска. Момент инерции
тонкого кольца найдется по формуле
dJ=dmr2.
Момент инерции всего диска определяется
интегралом
,
гдеS= $\pi$ R2
- площадь всего диска. Момент инерции
тонкого кольца найдется по формуле
dJ=dmr2.
Момент инерции всего диска определяется
интегралом
![]()
Вычисление момента инерции тонкого стержня:
Пусть
тонкий стержень имеет длину l
и массу m.
Разделим его на малые элементы длины
dx
(рис.27), масса которых
![]() .
Если выбранный элемент находится на
расстоянии x от оси, то его момент инерции
.
Если выбранный элемент находится на
расстоянии x от оси, то его момент инерции![]() ,
т.е.
,
т.е.![]() Интегрируя
последнее соотношение в пределах от 0
до l/2
и удваивая полученное выражение (для
учета левой половины стержня), получим
Интегрируя
последнее соотношение в пределах от 0
до l/2
и удваивая полученное выражение (для
учета левой половины стержня), получим
![]()
Момент
инеpции обручаотносительно оси,
пpоходящей чеpез центp кольца пеpпендикуляpно
к его плоскости. В этом случае все
элементаpные массы обруча удалены от
оси на одинаковое pасстояние, поэтому
в сумме (3.18) r2 можно вынести за знак
суммы, т. е.![]()
Теорема Штейнера:
В общем случае вращения тела произвольной формы вокруг произвольной оси, вычисление момента инерции может быть произведено с помощью теоремы Штейнера: момент инерции относительно произвольной оси равен сумме момента инерции J0 относительно оси, параллельной данной и проходящей через центр инерции тела, и произведения массы тела на квадрат расстояния между осями: J=J0+ma^2.
Например,
момент инерции диска относительно оси
О' в соответствии с теоремой Штейнера:
![]()
17. Момент инерции однородного тела вращения. Моменты инерции конуса, шара.
Линия
![]() - ось вращения.
- ось вращения.
![]() - масса на квадрат радиуса окружности,
по которой движется материальная точка.
- масса на квадрат радиуса окружности,
по которой движется материальная точка.
Все
тело мысленно разбиваем на маленькие
объемы. Масса этого кусочка
![]() .
.
![]()
Твердое тело представляется как совокупность системы точечных масс.
![]() - расстояние, на котором находится точка
от оси вращения.
- расстояние, на котором находится точка
от оси вращения.
![]()
![]() - общий алгоритм определения собственного
момента инерции твердого тела, относительно
оси проходящей через центр инерции
данного тела.
- общий алгоритм определения собственного
момента инерции твердого тела, относительно
оси проходящей через центр инерции
данного тела.
Момент инерции шара.
Сплошной шар массы m и радиуса R можно рассматривать как совокупность бесконечно тонких сферических слоев с массами dm , радиусом r, толщиной dr (рис.35).

Рассмотрим
малый элемент сферического слоя $\delta$
m с координатами
x, y, z.
Его моменты инерции относительно осей
проходящих через центр слоя - $\delta$
Jx,
$\delta$ Jy,
$\delta$ Jz,
равны
![]() Т.
е. можно записать
Т.
е. можно записать
![]() (п.26)
(п.26)
Так как для
элементов сферического слоя x2+y2+z2=r2
то
![]() После
интегрирования по всему объему слоя
получим
После
интегрирования по всему объему слоя
получим
![]() (п.27)
(п.27)
Так как, в силу
симметрии для сферического слоя
dJx=dJy=dJz=dJ
, а
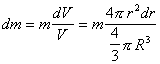 ,
то
,
то![]() Интегрируя по всему объему шара,
получаем
Интегрируя по всему объему шара,
получаем![]() Окончательно
(после интегрирования) получим, что
момент инерции шара относительно оси,
проходящей через его центр равен
Окончательно
(после интегрирования) получим, что
момент инерции шара относительно оси,
проходящей через его центр равен
![]()
Разобьём КОНУС на цилиндрические слои ось толщиной dr. Масса такого слоя dm = r2dr,
где ρ – плотность материала, из которого изготовлен конус. Момент инерции этого слоя dI = dm.r2.
Момент инерции всего конуса складывается из моментов инерции всех слоёв:
I
=
![]() =
=
![]() ρπ
r
4
dr
=
ρπ
r
4
dr
=
![]() ρR5.
ρR5.
Остаётся выразить
его через массу всего цилиндра:
m
=
![]() =
=
![]() =
=
![]() R3,
R3,
отсюда ρ
=
![]() ,
I
=
,
I
=
![]() =
=
![]() mR2.
mR2.
