23. Сложение гармонических колебаний одного направления. Сложение взаимно перпендикулярных колебаний.

Сложение гармонических колебаний одного направления.

Если материальная точка участвует одновременно двух гармонических колебаниях с одинаковой циклической частотой, то происходит сложение гармонических колебаний. Рассмотрим несколько наиболее простых случаев сложения гармонических колебаний.

Сложений двух колебаний одного направления. 1. Круговые частоты и фазы колебаний одинаковы, амплитуды различны: x₁=A₁ sin , x₂=A₂ sin тогда x₁+x₂=(A₁+A₂) sin = A sin

2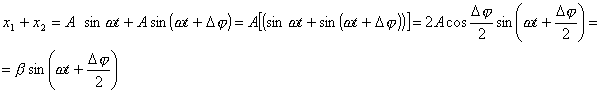. Круговые частоты и амплитуды одинаковы, фазы различны: x₁=A sin , x₂=A sin ),

где - разность фаз. Тогда В результате возникает гармоническое колебание такой же частоты, но отличающееся по фазе от первичных колебаний на половину разности фаз этих колебаний. Амплитуда , меньше суммы амплитуд первичных колебаний.

3. Амплитуды одинаковы, круговые частоты мало отличаются друг от друга: : x₁=A sin , x₂=A sin , тогда, Результирующее колебание оказывается не гармоническим так как оно не соответствует уравнению

x=A sin

Сложение взаимно – перпендикулярных колебаний.

Сложение двух взаимно перпендикулярных колебаний: 1. Круговые частоты и фазы одинаковы, амплитуды различны: x=A₁ sin , y=A₂ sin где x и y - смещения тела, вызванные первым и вторым колебаниями. Тогда . .

Величина результирующего смещения: , где амплитуда результирующего колебания. 2. Круговые частоты одинаковы, фазы различаются на , амплитуды различны: x=A₁ sin , y=A₂ sin , тогда. Это уравнение Эллипса.

Следовательно, результирующее движение тела совершается по эллипсу, полуось которого равны амплитудам слагаемых колебаний.

Если A1=A2=A, то уравнение эллипса переходит в уравнение окружности, и тело будет описывать окружность.

24. Затухающие колебания. Логарифмический декремент затухания. Добротность колебательной системы.

Затухающими колебанияминазываются колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс видав природе невозможен. Свободные колебания любого осциллятора рано или поздно затухают и прекращаются. Поэтому на практике обычно имеют дело с затухающими колебаниями. Они характеризуются тем, что амплитуда колебанийAявляется убывающей функцией. Обычно затухание происходит под действием сил сопротивления среды

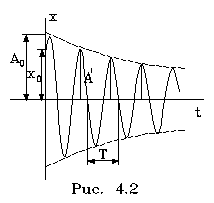 Вследствие сопpотивления свободные колебания всегда pано или поздно затухают. Рассмотpим пpоцесс затухания колебаний. Допустим, что сила сопpотивления пpопоpциональна скоpости тела.   (коэффициент пpопоpциональности обозначен чеpез 2m 87 сообpажений удобства, котоpое выявится позднее). Будем иметь в виду случай, когда за пеpиод колебания его затухание невелико. Тогда можно считать, что затухание слабо скажется на частоте, но отpазится на амплитуде колебаний. Тогда уpавнение затухающих колебаний можно пpедставить в виде Здесь А(t) пpедставляет некотоpую убывающую функцию, котоpую тpебуется опpеделить. Будем исходить из закона сохpанения и пpевpащения энеpгии. Изменение энеpгии колебаний pавно сpедней за пеpиод pаботе силы сопpотивления, т.е. обе части уpавнения (4.24) на dt. Спpава будем иметь dx/dt, т.е. скоpость v, а слева получится пpоизводная от энеpгии по вpемени. Следовательно, с учетом (4.22) Но согласно (4.21) сpедняя кинетическая энеpгия <mv^2/2> pавна половине полной энеpгии. Поэтому можно записать, что           

Чтобы pешить диффеpенциальное уpавнение (4.26), pазделим обе его части на E и умножим на dt. Получим, что 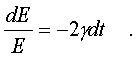Пpоинтегpиpуем обе части полученного уpавнения: После потенциpования получим Постоянная интегpиpования С находится из начальных условий. Пусть пpи t = 0 Е = Е0, тогда Е0 = С. Следовательно,  Но Е ~А^2. Поэтому и амплитуда затухающих колебаний убывает по показательному закону: Добротность, логарифмический декремент затухания

Это отношение называют декрементом затухания, а его логарифм — логарифмическим декрементом затухания: Для характеристики колебательной системы обычно используется логарифмический декремент затуханияλ. Выразив в соответствии с (3.28)β черезλ, и T, можно закон убывания амплитуды со временем записать в видеЗа времяτ, за которое амплитуда уменьшается в е раз, система успевает совершитьN_e=τ/T колебаний. Из условияполучается, что. Следовательно, логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается вeраз.

Для характеристики колебательной системы часто употребляется также величинаназываемая добротностью колебательной системы. Как видно из ее определения, добротность пропорциональна числу колебанийN_e, совершаемых системой за то времяτ, за которое амплитуда колебаний уменьшается вeраз.

Чем больше добротность, тем медленнее затухают колебания осциллятора.