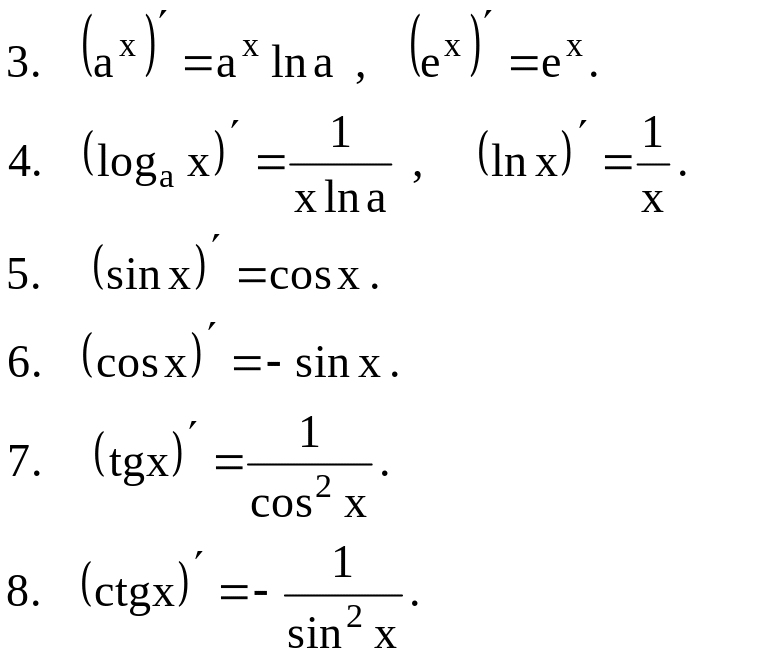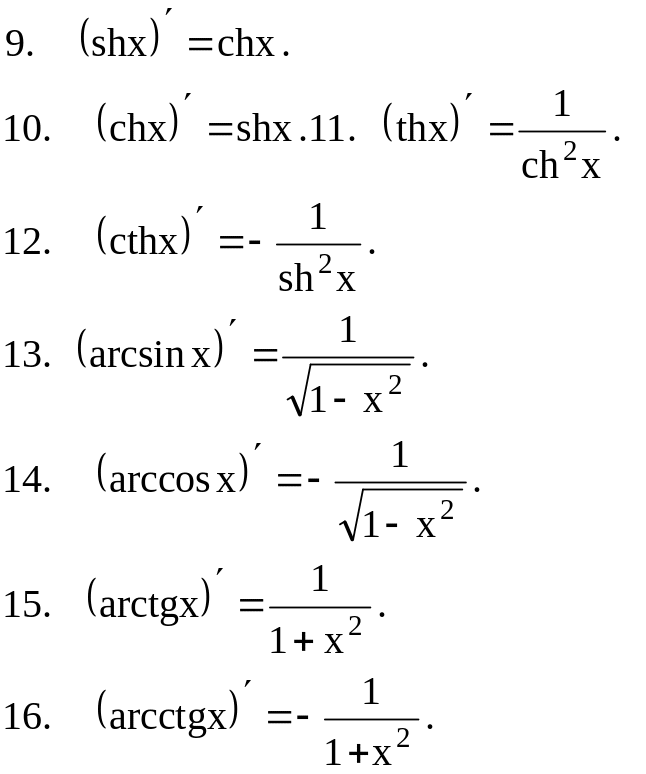1. Дифференцирование сложной функции

Пусть функция дифференцируема в точке , , функция дифференцируема в точке , тогда сложная функция дифференцируема в и её производная равна

.

2. Таблица производных основных элементарных функций

Эту таблицу необходимо знать наизусть.

С помощью этой таблицы и правил вычисления производных можно вычислить производную любой элементарной функции.

Понятие дифференциала функции

Определение. Если приращение функции в точке можно представить в виде , где - число, а - б.м. при , то величина называется дифференциалом функции в точке (главной частью приращения).

Теорема (о дифференциале). Для того, чтобы функция имела дифференциал в точке , необходимо и достаточно, чтобы существовала производная , при этом . (т.е. ).

Из этой теоремы становится ясным, почему существование производной у функции и существование дифференциала называются одним словом- дифференцируемость.

Осн. лит.: 2, [127-150], 19, [52-58], 18, [235-265], 20, [157-187]

Доп. лит.: 30, [180-188].

Контрольные вопросы:

1.Сформулируйте определение производной.

2. Каков ее механический и геометрический смысл?

3.Сформулируйте определение дифференциала функции?

Лекция № 9. Исследование поведения функции и их графиков.

Определение. Точка x₀ , в которой f(x₀) непрерывна, а производная функции y=f(x) равна нулю или не существует, называется критической точкой этой функции.

Теорема (необходимое условие экстремума). Пусть x₀ – экстремальная точка функции y=f(x), тогда x₀ – критическая точка этой функции.

Теорема (достаточное условие экстремума). Пусть функция y=f(x) непрерывна в окрестности U(x₀) критической точки x₀ и дифференцируема в U(x₀) кроме быть может самой точке x₀. Тогда

1) если в U(x₀) f ' (x)>0 при х<x₀ и f '(x)<0 при x>x₀ , то x₀  точка максимума;

2) если в U(x₀) f ' (x)<0 при х<x₀ и f '(x)>0 при x>x₀ , то x₀  точка минимума;

3) если в U(x₀) f ' (x)>0 или f '(x)<0 при x x₀ , то в x₀  экстремума нет.

Теорема. Пусть функция y=f(x) дифференцируема в некоторой окрестности критической точки х₀ и f ''(x₀) существует. Тогда, если f ''(x₀)>0, то x₀ - точка минимума, а если f ''(x₀)<0, то x₀ - точка максимума.

Выпуклость и точки перегиба

Определение. Функция y=f (x) называется выпуклой вниз (вверх) в интервале (a,b), если для любого x₀(a,b) значение функции в х(a,b) не меньше (не больше) соответствующей ординаты касательной к графику функции, проведенной в точке (x₀, f (x₀)).

Теорема. Пусть функция y=f(x) дважды непрерывно дифференцируема в (a,b). Эта функция выпукла вниз (вверх) на этом интервале тогда и только тогда, когда f ''(x)0 (f ''(x) 0) x(a,b).

Определение. Точка х₀ называется точкой перегиба для функции y = f (x), если в некоторой окрестности этой точки график функции лежит по разные стороны от касательной к графику, проведенной в точки х₀, т.е. для х>x₀, y_ф-y_k  0, а для х < x₀, y_ф-y_k  0 или наоборот. Точку х₀, в которой имеется вертикальная касательная, называют точкой перегиба, если направления выпуклости функции по разные стороны от х₀ противоположны

Теорема (необходимое условие существования точки перегиба)

Пусть функция y=f(x) дважды непрерывно дифференцируема в U(x₀)\{x₀} и непрерывна в х_0. Тогда → если → → точка → перегиба →то или не существует.

Теорема (достаточное условие существования точки перегиба). Пусть функция y=f(x) дважды непрерывно дифференцируема в U(x₀)\{x₀} и непрерывна в x₀, где x₀ – критическая точка второго порядка. Тогда, если при x<x₀ и x>x₀, f ''(x) имеет разные знаки, то x₀ – точка перегиба этой функции. Если же при x<x₀ и x>x₀, знаки f ''(x) совпадают, x₀ – не точка перегиба.