1. Замена переменной в неопределенном интеграле.

Теорема 1. Если функция непрерывна, функция непрерывно дифференцируема, то . (1)

2. Метод подведения под знак дифференциала

Этот метод является наиболее часто используемым видом замены переменной, при котором один из сомножителей подинтегральной функции заносится под знак и объявляется новой переменной. Напомним, что подвести функцию под знак дифференциала - это значит записать после знака первообразную функции, т.е. .

3. Метод интегрирования по частям

Теорема 2. Пусть функции и непрерывно дифференцируемы, тогда

, (3)

4. Интегрирование рациональных функций

4.1. Интегрирование функций, содержащих квадратный трехчлен.

Здесь мы рассмотрим метод нахождения интегралов вида

и .

Выносим из квадратного трехчлена коэффициент и выделяем в нем полный квадрат следующим образом:

где .

Делаем в интеграле замену переменной , , в результате он приводится к виду

или .

Записываем интеграл в виде суммы двух интегралов в соответствии с двумя слагаемыми числителя. В первом интеграле делаем замену переменной . В результате оба слагаемых - табличные интегралы.

4.2. Интегрирование рациональных функций

Теорема. Каждая правильная рациональная дробь может быть представлена в виде суммы конечного числа следующих четырех типов:

1⁰. 2⁰.

3⁰. 4⁰.

где А, В – числовые коэффициенты; трехчлен не имеет вещественных корней (т.е. ).

5. Интегрирование некоторых тригонометрических функций

В этом пункте мы рассмотрим нахождение интегралов вида

,

где - рациональная функция относительно .

Проверим, что такие интегралы с помощью универсальной замены переменной

всегда сводятся к интегралам от рациональных функций. В самом деле

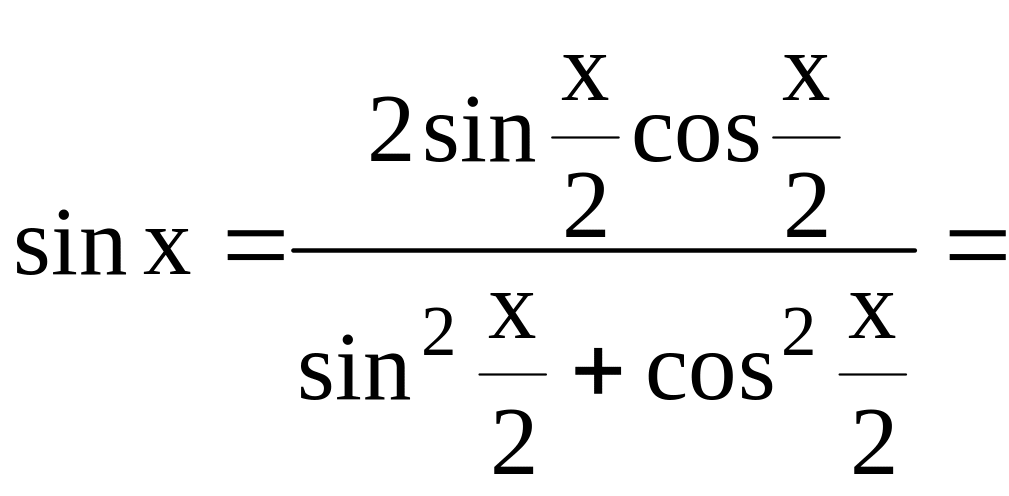
разделим числитель и знаменатель

дроби на .

.

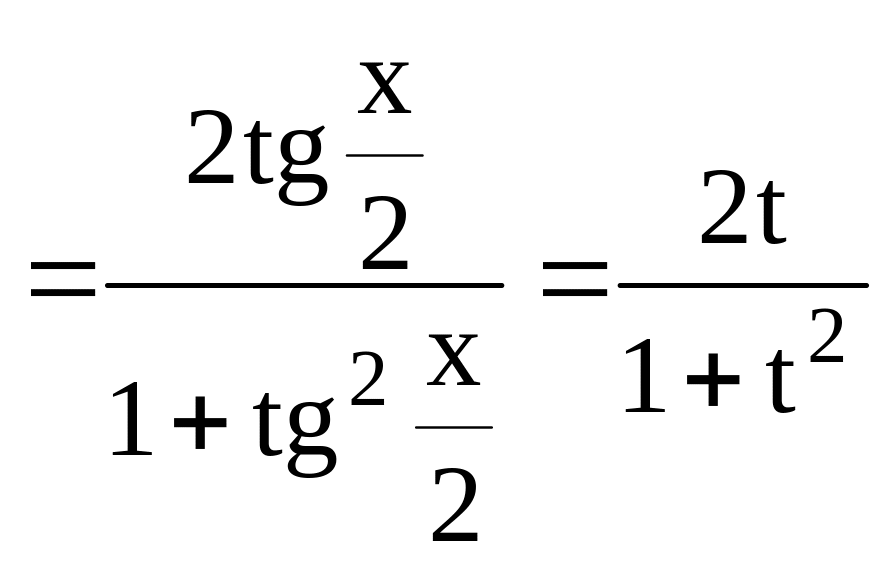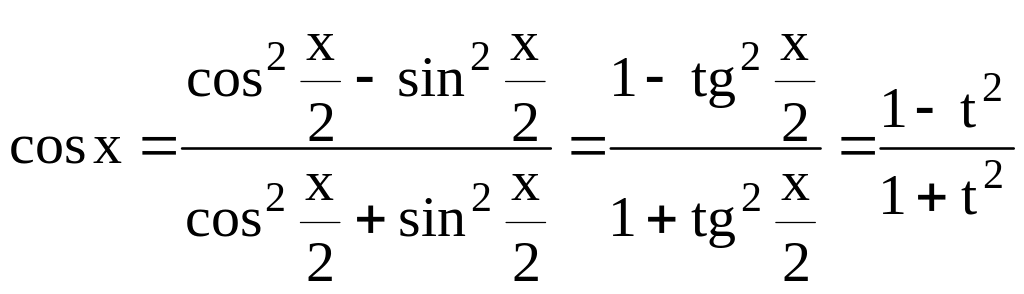Так как , то .

В результате получаем, что

где - рациональная функция.

Осн. лит.: 2, [208-213] , [224-231], 21, [345-366]

7, [189-196], 18, [498-508]

Контрольные вопросы:

1. Замена переменной в неопределенном интеграле

2. Формула интегрирования по частям

3. Интегрирование рациональных функций.

4. Какая подстановка называется универсальной тригонометрической?

Лекция № 12. Определенный интеграл как предел интегральных сумм. Формула Ньютона – Лейбница. Свойства определенного интеграла

Определение определенного интеграла

Аппарат определенных интегралов возник, прежде всего, для решения задач о нахождении площадей плоских фигур, в настоящее время эти интегралы используются практически во всех технических науках для решения задач, в которых требуется находить суммы большого числа малых величин

Определение. Криволинейной трапецией называется область на плоскости , ограниченная осью , прямыми , , где и графиком непрерывной на функции (см. рисунок 1).

Для простоты можно считать, что , т.е. трапеция расположена выше оси . Приближенно площадь криволинейной трапеции можно найти, заменив ее суммой площадей прямоугольников с малыми основаниями и высотами, равными значениям функции в некоторых выбранных точках.

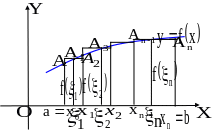
Рис 1

Определение. Разбиением отрезка на частей называется набор чисел из этого отрезка, где и .

В каждом отрезке (элементарном участке) разбиения выберем некоторую точку , где

Такое разбиение будем обозначать буквой , а длину элементарного участка через . Пусть на отрезке определена некоторая функция .

Определение. Интегральной суммой для функции , построенной по разбиению отрезка , называется сумма произведений значений функции в выбранных точках на длины элементарных участков.

Такую сумму будем обозначать через .

Если , то интегральная сумма равна площади ступенчатой фигуры, составленной из прямоугольников с основаниями и высотами (см. рис 1), т.е. приближенно равна площади соответствующей криволинейной трапеции.

Определение. Определенным интегралом от функции на отрезке называется предел интегральных сумм этой функции по разбиениям , у которых максимальный стремится к нулю, т.е.

.

Если на , то этот интеграл выражает точную площадь соответствующей криволинейной трапеции.

Теорема 1. Если функция непрерывна на или имеет на этом отрезке конечное число точек разрыва первого рода, то эта функция интегрируема на , т.е. существует.

Смысл этой теоремы состоит в том, что при выполнении условий теоремы, при любых разбиениях, у которых длины всех участков стремятся к нулю, интегральные суммы стремятся к одному и тому же числу .

Свойства определенного интеграла

В дальнейшем будем считать, что все рассматриваемые функции интегрируемы.

1) , - постоянная.

2) Если на , то .

3) Если на отрезке функция ограничена снизу и сверху числами и , т.е. если на , то .

Формула Ньютона – Лейбница

Теорема 1. (Ньютона - Лейбница)

Пусть функция непрерывна в отрезке и функция есть ее первообразная на этом отрезке, тогда .

Часто разность здесь записывают в сокращенном виде: .

Пример 1.

.

Осн. лит.: 1, [5-33] , 6, [12-42], 19, [52-58].

Доп. лит.: 30, [151-168].

Контрольные вопросы:

1. Определение определенного интеграла

2. Свойства определенного интеграла

3. Формула Ньютона-Лейбница

Лекция 13. Приложения определенных интегралов

С помощью определенных интегралов можно находить площади плоских фигур при различных способах задания границ области, длины дуг кривых, объемы тел и площади поверхностей вращения.

1. Площадь в декартовых координатах.

Площадь области , ограниченной линиями и графиками непрерывных на функций , где на , находится по формуле

2.Нахождение длины дуги кривой

Теорема. График непрерывно дифференцируемой на функции спрямляем, и его длина находится по формуле .

3. Вычисление объемов тел вращения с помощью определенных интегралов

В случае, если тело T образовано вращением криволинейной трапеции, задаваемой непрерывной функцией на вокруг , площадь круга находится по формуле , т.к. есть радиус этого круга. Объем указанного тела вращения определяется соотношением .

4. Нахождение площади поверхности вращения

Пусть график непрерывно дифференцируемой функции , где и , вращается вокруг оси . Можно доказать, что площадь получившейся поверхности вращения находится по формуле

.

Осн. лит.: 2, [275-292], 19, [66-77]

21, [396-429], 7, [355-382]

Контрольные вопросы:

1. Формула Ньютона-Лейбница.

2.Вычисление площадей с помощью определенного интеграла.

3.Длина дуги кривой.

4.Вычисление объема тела вращения.

Лекция № 14. Дифференциальные уравнения первого порядка

Определение. Дифференциальным уравнением называется уравнение, связывающее независимую переменную , искомую функцию и ее производные т.е. уравнения вида где непрерывная функция переменных.

Если искомая функция есть функция одной независимой переменной, то дифференциальное уравнение называется обыкновенным.

Например,

Если искомая функция зависит от нескольких независимых переменных, то дифференциальное уравнение называется уравнением в частных производных.

Например,

В дальнейшем будем рассматривать лишь обыкновенные дифференциальные уравнения.

Порядком дифференциального уравнения называется порядок наивысшей производной, явно входящей в уравнение.

Например: - дифференциальное уравнение 1- го порядка;

- дифференциальное уравнение 2- го порядка;

- уравнение 9- го порядка.

Решением дифференциального уравнения (2.1) называется функция которая при подстановке в дифференциальное уравнение обращает его в тождество.

Процесс отыскания решений дифференциального уравнения называется интегрированием уравнения.

График решения дифференциального уравнения называется интегральной кривой этого уравнения.