2.3 Планы практических занятий

Модуль-1. Линейная алгебра и аналитическая геометрия.

Практическое занятие № 1. Определители и матрицы.

Задания АЗ-1.1: [14], часть 1, №№1-3, АЗ-1.2: [14], часть 1, №№1-2,

АЗ-1.3: [14], часть 1 №№1-2.

Методические рекомендации. Для решения данных задач АЗ-1.1 можно использовать формулы для вычисления определителей второго и третьего порядков. А также использовать методы вычисления определителей – приведение к треугольному виду и разложение определителя по элементам некоторого ряда. При решении задач АЗ-1.2 и АЗ-1.3 рекомендуется воспользоваться правилами проведения операции над матрицами и формулой вычисления обратной матрицы к заданной.

Пример1. Вычислить определитель n-го порядка:

Р ешение:

.

Пример 2. Вычислить АВ и ВА. Проверить равны ли произведения эти матриц.

.

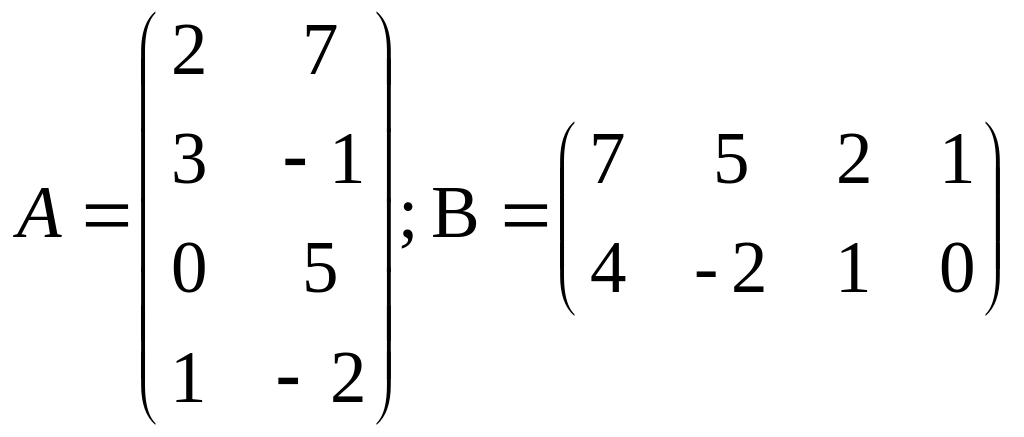Решение:

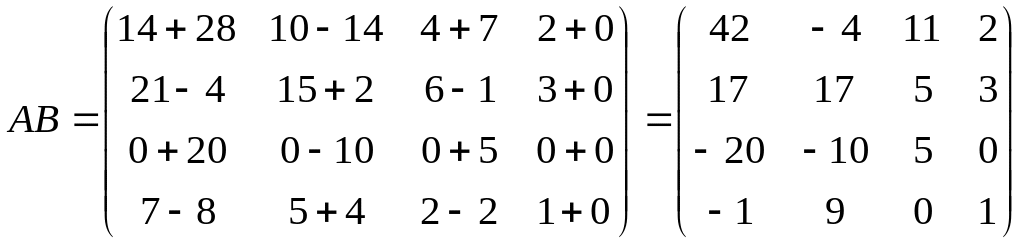
размерность матрицы -(4 4)

размерность матрицы - (2 2)

Пример 3. Найти обратную матрицу А матрицы А=

Решение: detA=40 0 матрицы А невырожденная можно найти А

Найдены A =(-1) M элементов а .

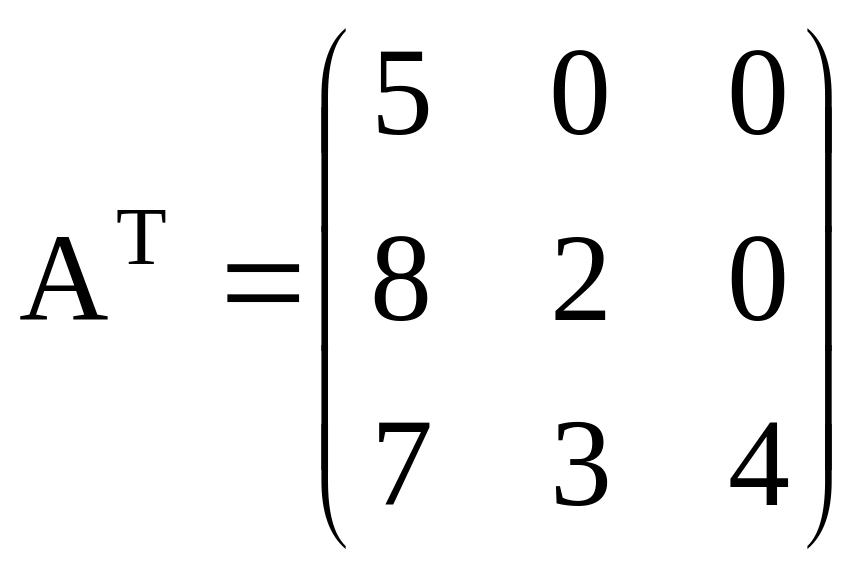- транспонированная матрица, -присоединенная матрица,

Тогда .

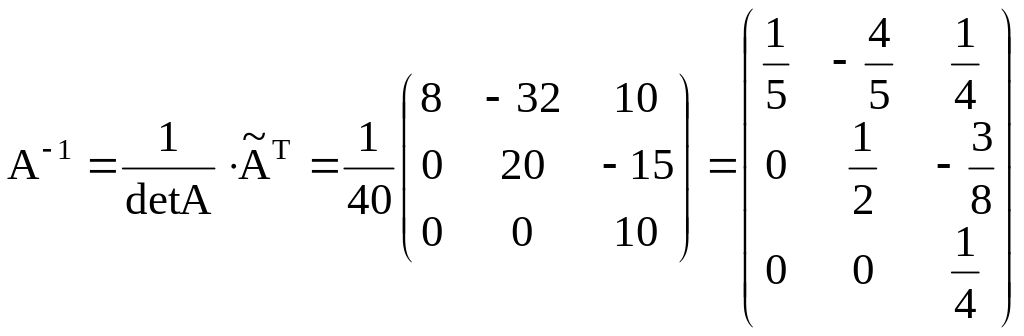Теперь проверим

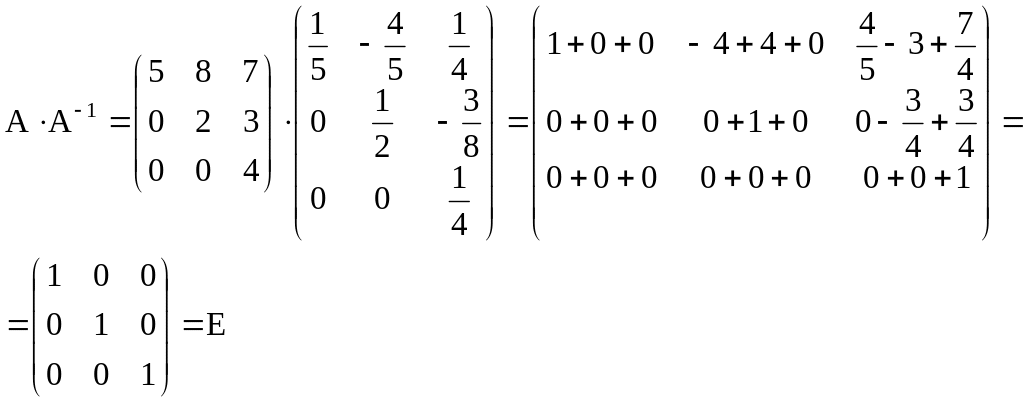
Пример 4. Найти ранг матрицы

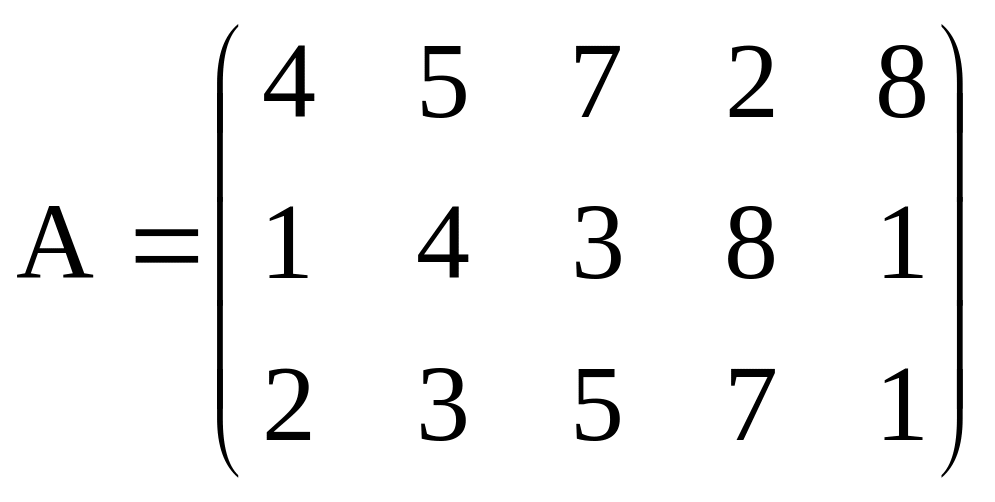
Решение: а) методом элементарных преобразований

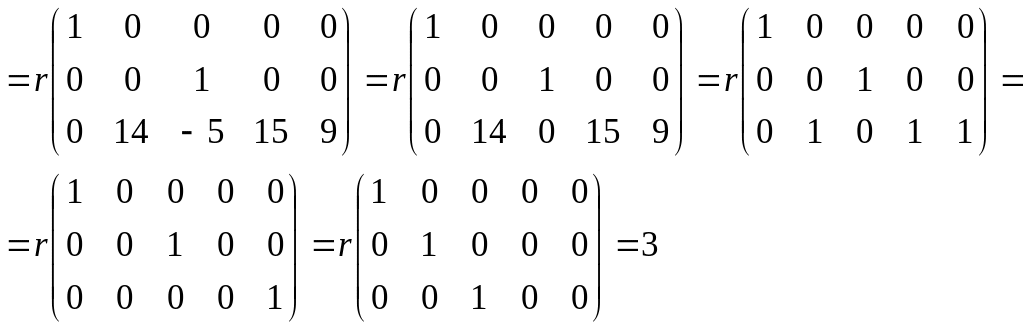
в) методом окаймляющих миноров. Фиксируем ненулевой минор 2-го порядка

Рассмотрим окаймляющий минор 3-го порядка

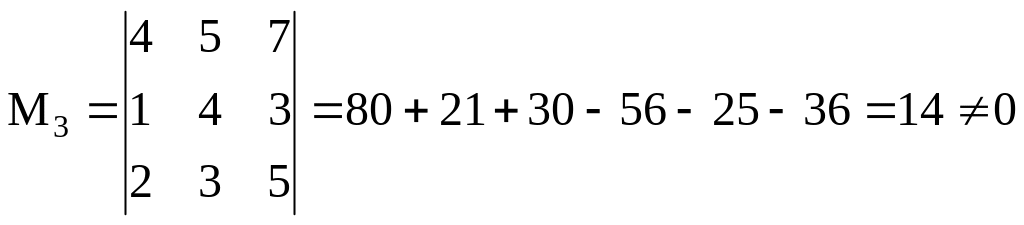
- нельзя составить .

Осн.лит.: 14, часть 1, [9-7].

Доп. лит: 29, [182-188].

Контрольные вопросы:

1. Какие свойства определителей используются при их вычислении? Укажите основные правила вычисления определителей.

2. Приведите основные операции над матрицами. Как умножить матрицу на число? Как перемножаются матрицы?

3. Какими методами вычисляется ранг матрицы? Какой цели служит ранг матрицы?

Практическое занятие № 2. Система линейных алгебраических уравнений.

Задания. АЗ-1.4: [14] , часть1, №№1-3, 5.

Методические рекомендации. Прежде чем решать систему линейных алгебраических уравнений (СЛАУ) нужно исследовать ее на совместность. Если для системы и то можно использовать формулы Крамера или матричный метод. Если же и то целесообразно пользоваться алгоритмом метода Гаусса.

Пример 1. Проверить совместность системы линейных уравнений.

Рассмотрим систему трех уравнений с тремя неизвестными

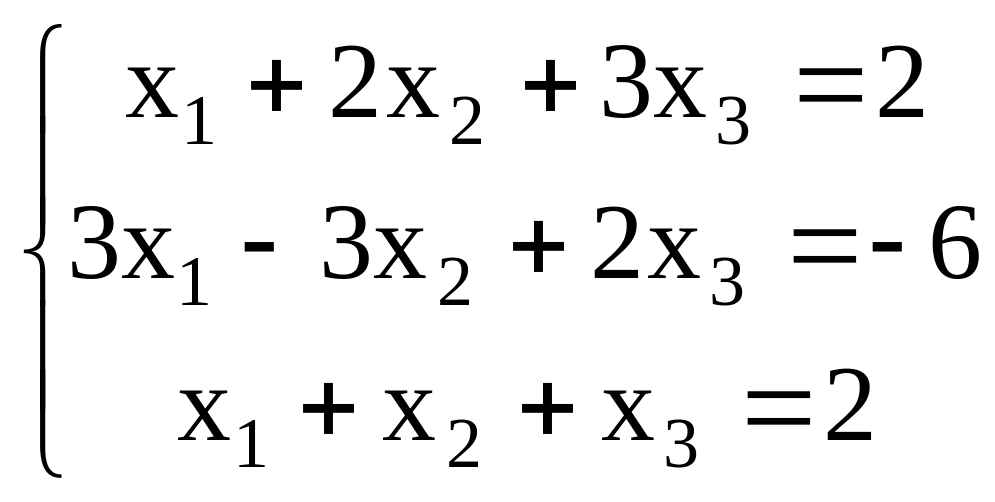
Решение: , , 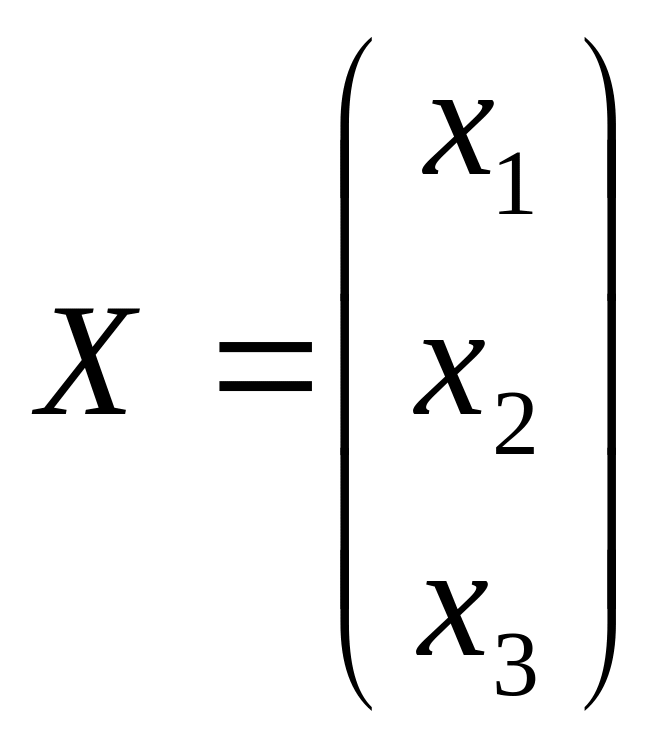- матричная форма системы.

Проверим совместность системы по теореме Кронекера-Капелли

,

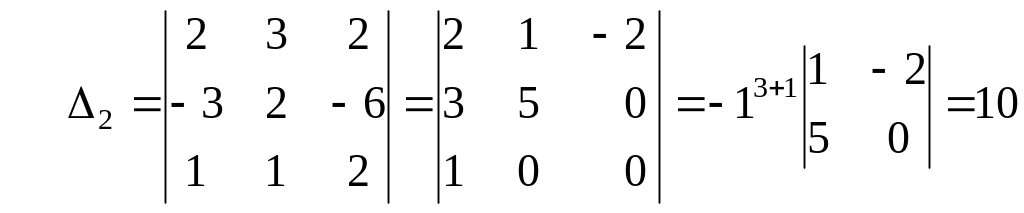
методом окаймляющих миноров, получим

, - система совместна и имеет единственное решение.

Пример 2. Решить систему уравнений.

а) методом Гаусса; б) методом Крамера, в) матричным методом.

Решение:

а) 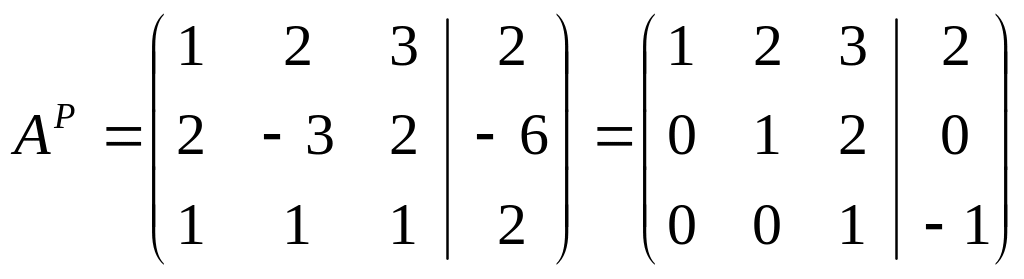, , т.е. .

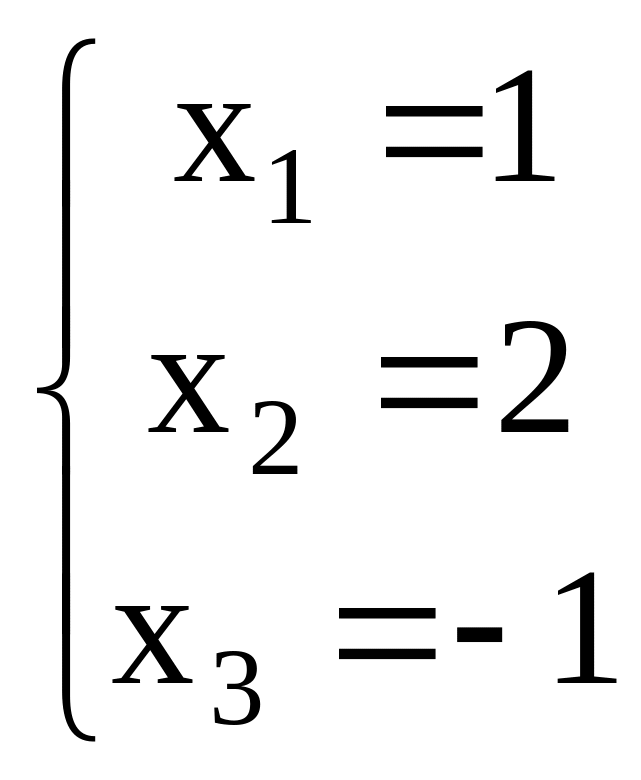б) методом Крамера ,

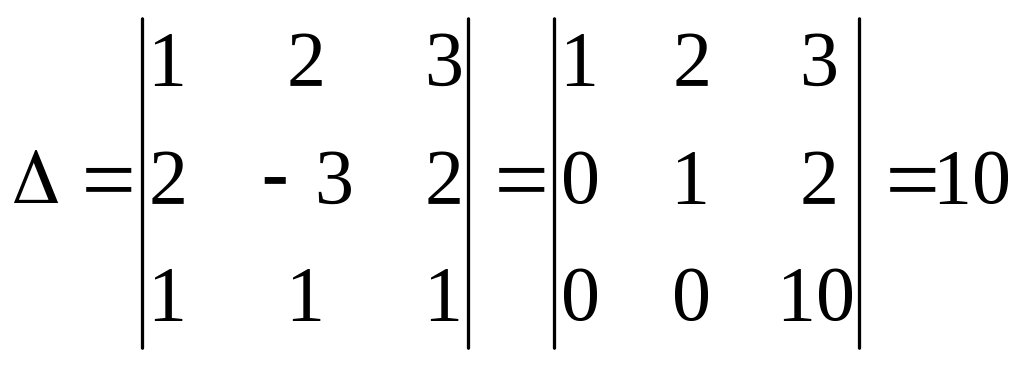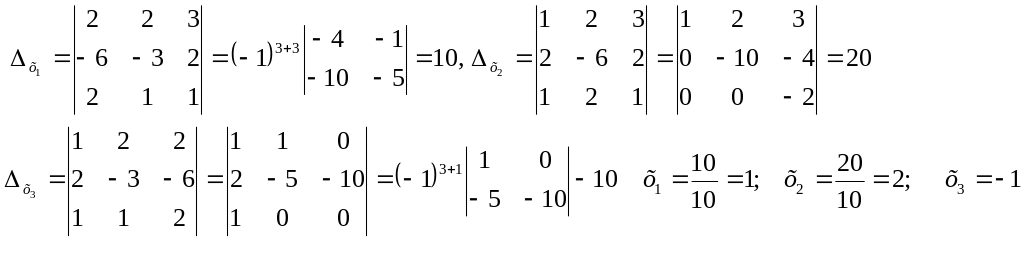в) матричным методом

матрица А невырожденная

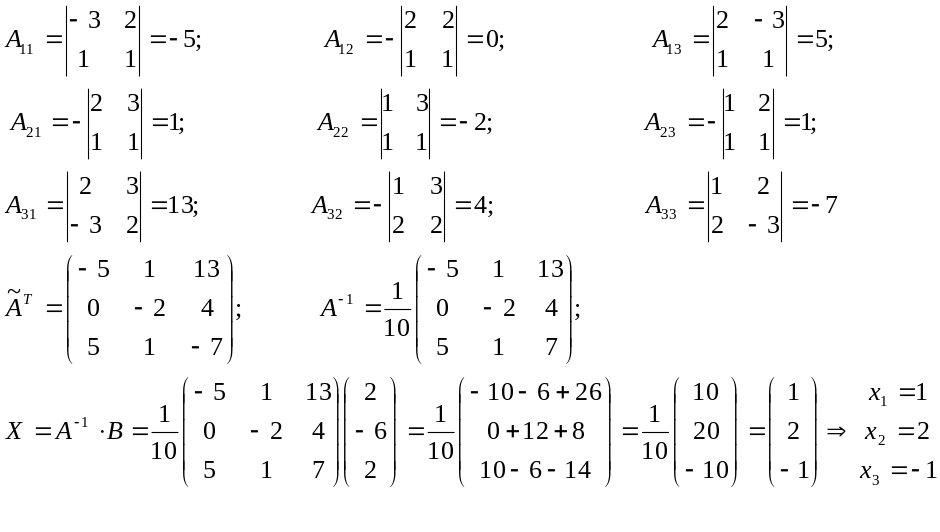
Осн. лит. 14, [27-33]

Доп.лит. 29, [189-192].

Контрольные вопросы:

1. Как определить совместность СЛАУ?

2. Использование метода Гаусса при .

3. Как найти все множество решений неоднородной СЛАУ?

Практическое занятие № 3. Векторная алгебра. Скалярное, векторное и смешанное произведение векторов.

Задания. АЗ-2.1: [14], часть 1, №№1-8, АЗ-2.2 [14] ,часть 1, №№1-7, АЗ-2.3 [14], №№1-7.

Методические рекомендации. При решении задач рекомендуется использовать правила вычисления координат векторов их длин, проекции вектора на ось, а также линейные операции над векторами. Для вычисления координат вектора в новом базисе используются определения линейной зависимости и независимости векторов. Для вычисления скалярного произведения использовать его определение или формулу вычисления через координаты перемножаемых векторов. При нахождении векторного произведения необходимо учитывать условия которым должны удовлетворять данные вектор и формулу вычисления векторного произведения через их координаты. При вычислении смешанного произведения трех векторов необходимо использовать правила вычисление определителя третьего порядка.

Пример 1. Определить длину и направляющие косинусы радиуса вектора точки и вектора ; если

Решение: а) ,

б) ,

Пример 2. Даны векторы

Найти: а) вектор ; б) модуль ; с)

Решение:

а)

б)

в)

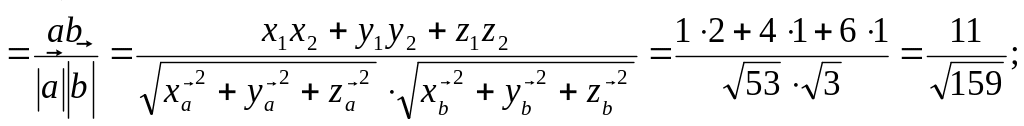
Пример 3. Доказать, что векторы образуют базис и найти координаты вектора в этом базисе, т.е. . Для векторов выполняется условие

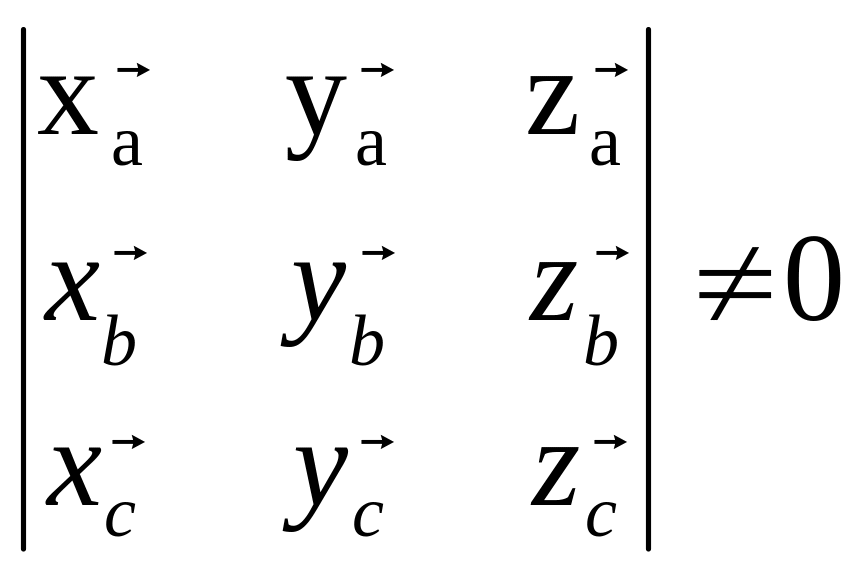, пусть

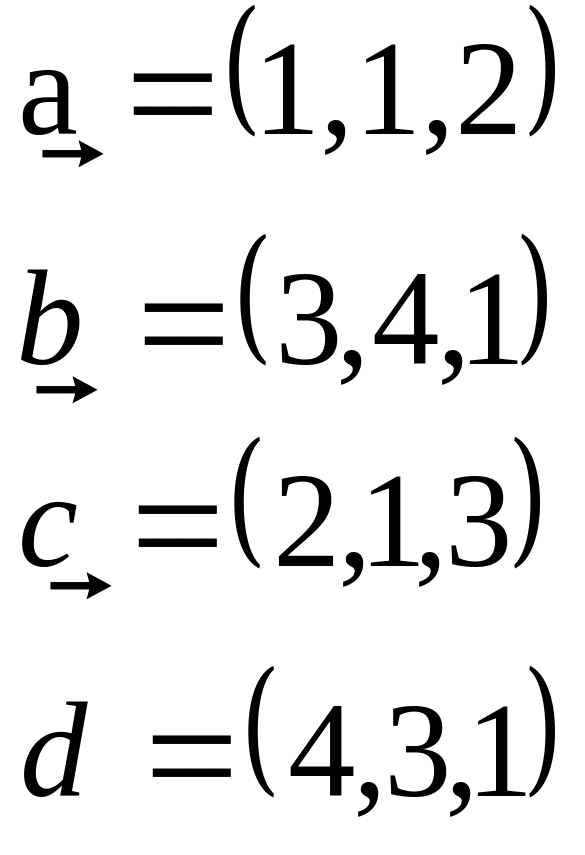
Решение: ,

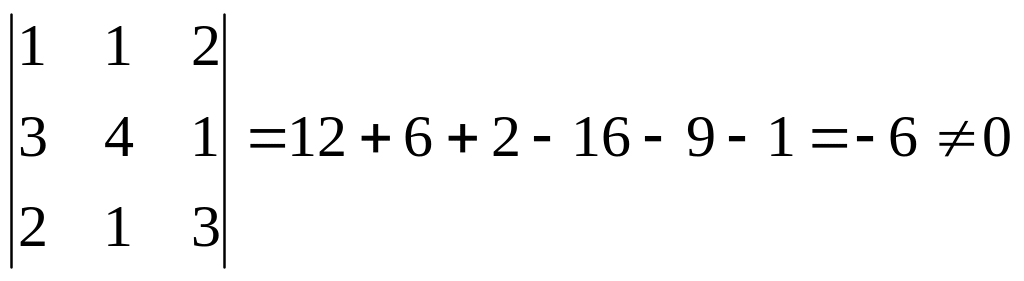если приравниваем X, Y, Z векторов к x, y, z векторам находим : .

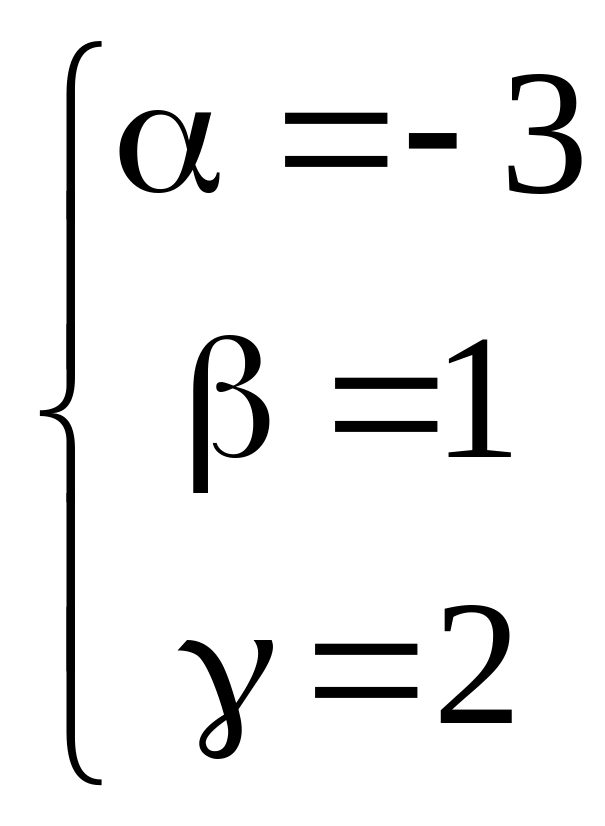
Пример 4. Вычислить скалярное произведение векторов, если .

Решение. По определению скалярного произведения получим .

Пример 5. Пусть найти .

Решение.

Пример 6. Даны точки и найти смешанное произведение векторов и .

Решение. Итак, и , .

Осн. лит. 14 , часть 1, [59-69].

Доп. лит.: 30, [41-142] .

Контрольные вопросы:

1. Привести формулу вычисления угла между двумя векторами через скалярное произведение этих векторов.

2. Какие свойства скалярного и векторного произведения используются при их вычислении?

3. Как вычисляются направляющие косинусы заданного вектора?

4. Какие условия должны выполняться для коллинеарности векторов?

Практическое занятие № 4. Прямая на плоскости.

Задания. АЗ-3.3: [14], часть 1 , №№. 1-8.

Методические рекомендации. Для задач на прямую на плоскости использовать различные виды уравнений прямой из лекции №5 и уметь переходить от одного вида к другому. Угловые коэффициенты прямых использовать для определения их взаимного расположения. При решении геометрических задач использовать формулу вычисления расстояния от данной точки до заданной прямой

Пример 1. Показать, что прямые и перпендикулярны.

Решение. Приводим уравнение каждой прямой к виду с угловым коэффициентом

и

Угловые коэффициенты этих прямых и . Так как , то прямые перпендикулярны.

Пример 2. Определить отрезки, отсекаемые осях координат прямой проходящей через точки и .

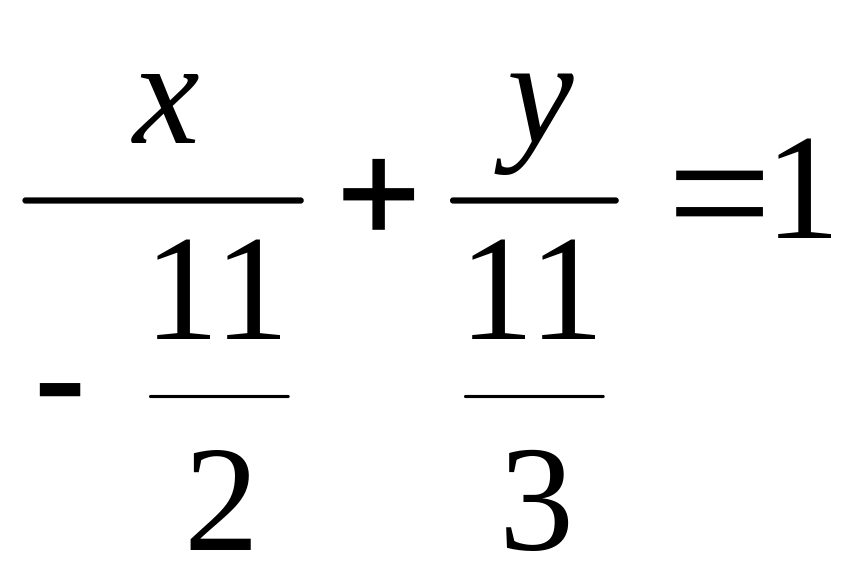
Решение. Уравнение прямой имеет вид или . Приведем это уравнение к виду “в отрезках” и и .

Пример 3. Даны прямая и точка . Найти расстояние от точки до прямой.

Решение:

.

Осн. лит. 14 , часть 1, [98-101].

Доп. лит. 29, [237-239].

Контрольные вопросы:

1. Как определить координаты нормального вектора прямой?

2. Как будут расположены прямые при равенстве нулю одного из коэффициентов общего уравнения прямой?

3. Какой вид уравнения прямой определяет отрезки отсекаемые на осях координат?

Практическое занятие № 5. Плоскость и прямая в пространстве.

Задания. АЗ-3.1: [14] , часть 1, №№. 1-4, АЗ-3.2: [14], №№. 1-3.

Методические рекомендации. Уравнение плоскости в пространстве составляется в зависимости от способа ее задания. При составлении уравнения прямой в пространстве учитываются координаты направляющего вектора. Взаимное расположение прямых и плоскостей в пространстве определяется расположением их направляющих и нормальных векторов. А углы между прямыми и плоскостями определяются через углы между этими векторами.

Пример 1. Дана плоскость . Привести данное уравнения плоскости к уравнению в отрезках на осях

Решение: Разделим общее уравнение плоскости на свободный член.

,

получаем уравнение в отрезках на осях.

Пример 2. Составить уравнение плоскости, проходящей через точку и отсекающей равные отрезки на осях координат.

Решение. Используя уравнение плоскости в отрезках, в котором , имеем . Координаты точки А удовлетворяют уравнению искомой плоскости, поэтому выполняется равенство , откуда . Итак, получаем уравнение .

Пример 3. Составить уравнения прямой, проходящей через точку и пересекающей ось Ох под прямым углом.

Решение. Так как прямая перпендикулярна оси Ох и пересекает ее, то она проходит через точку . Составив уравнения прямой, проходящей через точки и , получаем

Осн. лит. 14, [91 -98].

Доп. лит. 29, [244-247].

Контрольные вопросы:

1. Как определить угол между двумя плоскостями?

2. Привести условие параллельности и условие перпендикулярности плоскостей.

3. Как будут расположены плоскости при равенстве нулю одного из коэффициентов общего уравнения плоскости?

Практическое занятие № 6. Кривые второго порядка. Поверхности второго порядка

Задания. АЗ - 4.1: [14] , часть 1, №№1-7, АЗ - 4.2: [14] , часть 1, №№1-2.

Методические рекомендации. По заданному каноническому уравнению кривой второго порядка можно определить все характеристики (полуоси, фокусы, эксцентриситет, директрисы и асимптоты) согласно формулам Лекции 7. Из общего уравнения кривых и поверхностей второго порядка методом выделения полных квадратов и методом параллельных сечений можно определить вид кривой и поверхности.

Пример 1. Составить каноническое уравнение гиперболы, если ее фокусы лежат на оси и расстояние между ними равно 10, а длина оси по равна 8.

Решение: По условию задачи

- искомое уравнение.

Пример 2. Дано уравнение эллипса . Найти его оси, координаты центра и эксцентриситет.

Решение:

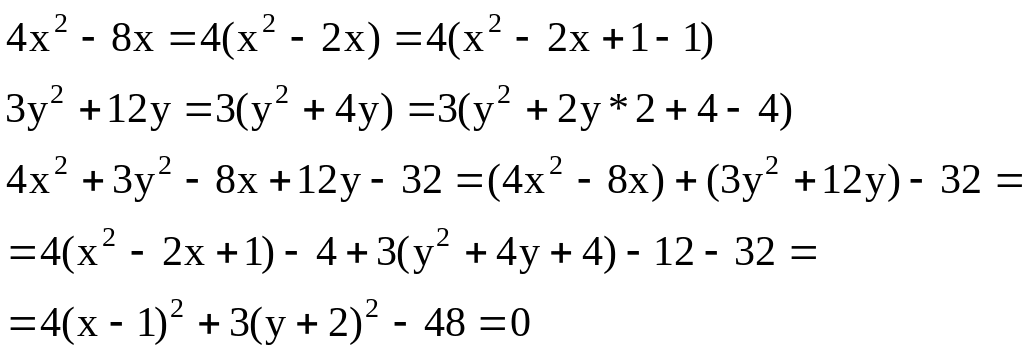
отсюда , получим уравнение эллипса с осями параллельными координатам с центром симметрии в точке (1,-2),

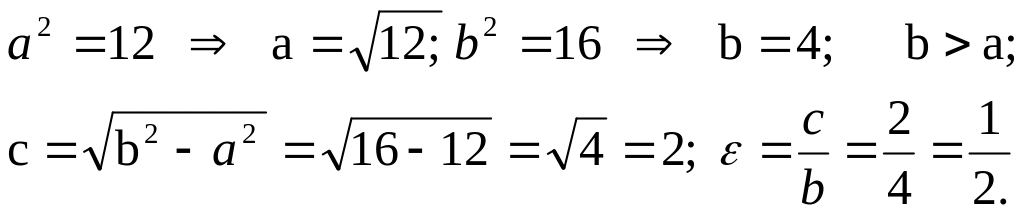
Пример 3. Какую поверхность определяет уравнение , сделать схематический чертеж.

Решение. Данное уравнение не содержит , поэтому рассматриваемая поверхность есть цилиндр с образующими, параллельными оси . Уравнение направляющей имеет вид:

Рис.2

Осн. лит. 14, часть 1, [120-130].

Доп. лит. 30, [239-243], [247-251].

Контрольные вопросы:

1.Как определяются фокусы кривой второго порядка?

2.Что характеризует эксцентриситет кривой второго порядка.

3. В чем различие сопряженной гиперболы от данной?

Модуль -2. Дифференциальное и интегральное исчисление функций одной

переменной.

Практическое занятие № 7. Введение в анализ. Функция. Вычисление пределов. Непрерывность.

Задания. АЗ – 5.1: [14], часть1, №№ 1-3., АЗ 5.2: [14], часть 1, №№ 1-5, АЗ 5.3: [14], часть 1, №№ 1-4, АЗ 5.4: [14] , часть 1, №№ 5-7.

Методические рекомендации. При решении практических задач данной темы знать понятие множества и уметь выполнять операции над множеством, т.к. понятие «функция» устанавливает зависимость между элементами множества. При анализе функции необходимо определять ее свойства – область определения, множество значений, четность и нечетность, периодичность и т.д. При нахождении предела функции используются методы непосредственного вычисления и устранения неопределенностей путем преобразования данного выражения, предельных переходов, использования замечательных пределов и их следствий. Непрерывность функции в точке устанавливается согласно определению. Для анализа возможных точек разрыва вычисляются односторонние пределы.

Пример 1. Найти область определения функции .

Решение. Функция определена, если и , т.е. если и . Тогда .

Пример 2. Установить четность или нечетность функций:

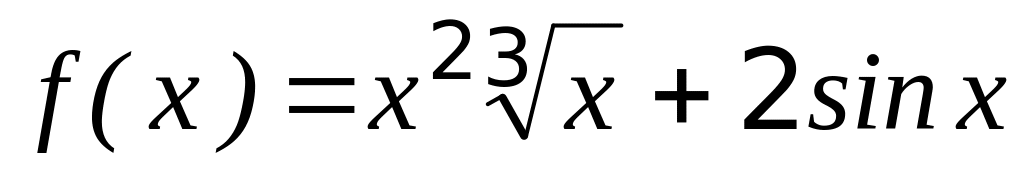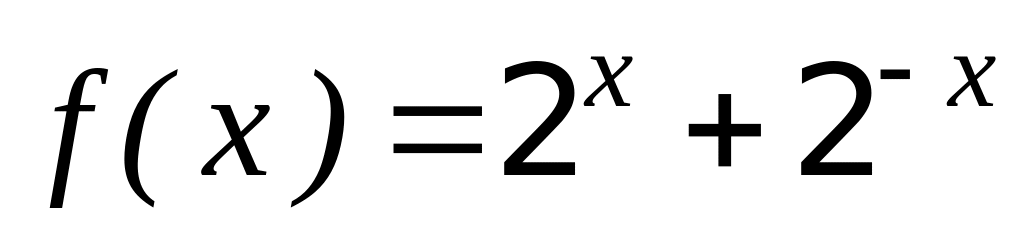1. ; 2) ; 3) ;

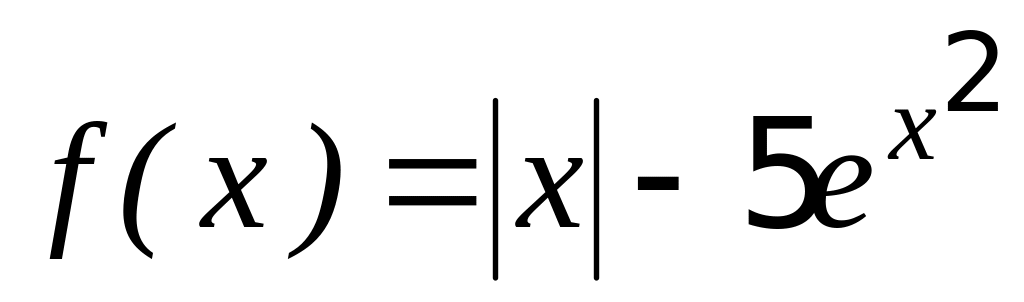Решение. 1) Заменяя на , получим

,

т.е. . Следовательно, функция – нечетная.

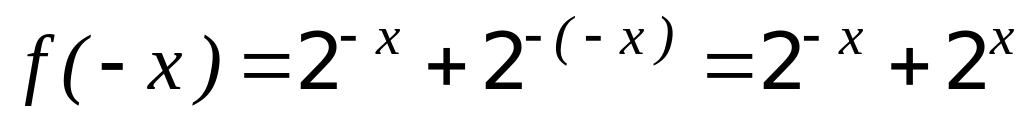2. Имеем , т.е. .

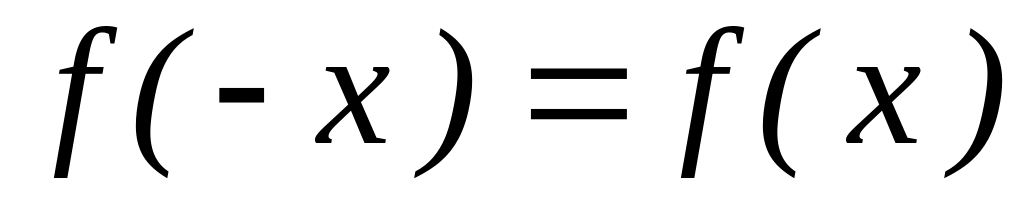Итак, функция – четная.

3) Рассмотрим , т.е. . Следовательно, функция – четная.

Пример 3. Найти .

Решение. Здесь неопределенность вида .

Разделим числитель и знаменатель дроби на старшую степень , т.е. на :

= = .

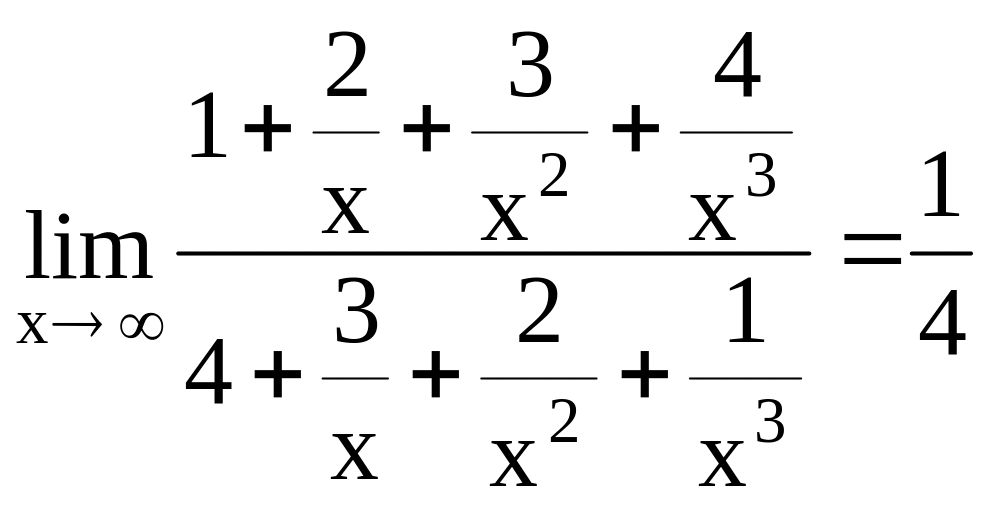Пример 4. Найти следующие пределы:

а) б) ;

Решение. Числители и знаменатели дробей будем заменять эквивалентными бесконечно малыми.

а) ~ , tg 8x ~ 8x, при , тогда .

б) ~ , ~  тогда .

Пример 5. Найти точки разрыва функций.

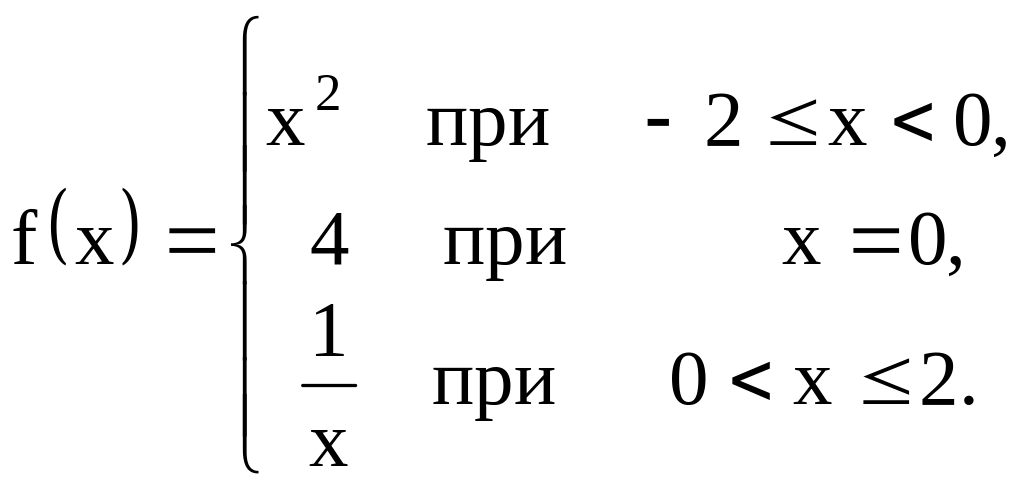
Решение. Каждая из трех функций непрерывны в области определения. Поэтому разрыв возможен только на стыке промежутков, то есть в точке .

Вычислим ,

следовательно, является точкой разрыва второго рода.

Осн.лит.: 14, часть 1, [156-165].

Доп. лит. 29, [255-257], [260-267].

Контрольные вопросы:

1. Предел какой последовательности определяет число ?

2. От чего зависит область определения функции?

3. Как сложную функцию представить в виде суперпозиции элементарных функции?

4. Как определяется периодичность функции и находится ее период?

Практическое занятие № 8. Производная и дифференциал.

Задания АЗ 6.1: [14], часть 1, №№ 1,2, АЗ 6.2: [14], часть 1, №№ 1-3, АЗ 6.3: [14], часть 1, №№ 1-3 АЗ 6.4: [14] ,часть 1, №№ 1-3.

Методические рекомендации. При нахождении производной функции необходимо применять правила дифференцирования и таблицу производных. Сложную функцию следует дифференцировать, разложив на элементарные, обратную по формуле и т.д. Производная n-го порядка определяется дифференцированием производной n-1 го порядка. Согласно определению дифференциала можно найти дифференциала любого порядка.

Пример 1. Найти производную функции .

Решение: Полагая и , имеем и . Отсюда получаем .

Пример 2. Найти производную

Решение. Преобразуем функцию .

Тогда .

Пример 4. Найти дифференциал второго порядка функции .

Решение: Имеем , . Тогда .

Осн. лит. 14, часть 1, [189-201]

Доп. лит. 29, [272-275].

Контрольные вопросы:

1. Как найти производную функции заданной параметрически?

2. В чем заключается геометрический и механический смысл производной первого порядка?

3. Сформулируйте алгоритм метода логарифмического дифференцирования.