
- •Министерство образования и науки республики казахстан
- •Учебная программа дисциплины – Syllabus
- •Данные о дисциплине:
- •1.5 Описание дисциплины
- •1.6 Контроль и оценка знаний.
- •Оценка знаний студентов
- •Содержание Активного раздаточного материала
- •Тематический план курса
- •2.2. Конспект лекционных занятий
- •Ранг матрицы
- •Определение. Системой из m линейных алгебраических уравнений с n неизвестными называется система вида:
- •Векторы и линейные операции над ними. Скалярное и векторное произведения. Смешанное произведение трех векторов.
- •Первый замечательный предел
- •Второй замечательный предел
- •1. Дифференцирование сложной функции
- •Асимптоты графика функции
- •1. Замена переменной в неопределенном интеграле.
- •2. Метод подведения под знак дифференциала
- •3. Метод интегрирования по частям
- •4. Интегрирование рациональных функций
- •4.1. Интегрирование функций, содержащих квадратный трехчлен.
- •4.2. Интегрирование рациональных функций
- •5. Интегрирование некоторых тригонометрических функций
- •Определение определенного интеграла
- •Дифференциальные уравнения первого порядка
- •Задача Коши. Теорема существования и единственности
- •Рассмотрим дифференциальное уравнение вида , где правая часть есть произведение функции, зависящей только от , на функцию, зависящую только от .
- •2.3 Планы практических занятий
- •Практическое занятие № 9. Исследование поведения функций и их графиков. Приложения дифференциального исчисления к геометрии.
- •Планы занятий в рамках самостоятельной работы студентов (срс)
- •2.7. Варианты тестовых заданий для самоконтроля
- •2.9 Экзаменационные вопросы по курсу
Практическое занятие № 9. Исследование поведения функций и их графиков. Приложения дифференциального исчисления к геометрии.
Задания. АЗ - 6.7 [14], часть 1, №№ 1-5, АЗ - 6.8 [14], часть 1, №№ 1.
Методические рекомендации. Для полного исследования поведения функции необходимо определить точки экстремума и точки перегиба графика данной функции с помощью производных. А для определения основных свойств функции нужно применить материал изложенный в Лекции 8. С помощью теории пределов находятся асимптоты и возможные точки разрыва графика функции.
Пример 1. Найти
интервалы возрастания и убывания функции
![]() .
Исследовать функцию на экстремум.
.
Исследовать функцию на экстремум.
Решение. Найдем
производную
![]() и стационарные точки, решая уравнения
и стационарные точки, решая уравнения
![]() .
Определим знак производной
.
Определим знак производной
![]() в окрестности точки
в окрестности точки
![]() :
:
![]() , при
, при
![]() и
и
![]() при
при
![]() .
Следовательно, в точке
.
Следовательно, в точке
![]() функция имеет минимум
функция имеет минимум
![]() .
Функция возрастает на интервале
.
Функция возрастает на интервале
![]() ;
убывает на интервале
;
убывает на интервале
![]() .
.
Пример 2. Найти
точки перегиба кривой![]() .
.
Решение. Находим
![]() ,
,
![]() .
Критическая точка второго рода:
.
Критическая точка второго рода:
![]() .
.
Определим знак
![]() в окрестности
.
в окрестности
.
Следовательно,
точка
![]() ,
т.е. (5,2) – точка перегиба.
,
т.е. (5,2) – точка перегиба.
Пример 3. Найти
асимптоты кривой
![]() .
.
Решение. Функция
определена в интервалах
![]() .
Имеем
.
Имеем
![]() ,
следовательно
,
следовательно
![]() - вертикальная асимптота. Горизонтальных
асимптот нет, так как предел
- вертикальная асимптота. Горизонтальных
асимптот нет, так как предел
![]() не является конечной величиной. Находим:
не является конечной величиной. Находим:
![]()
![]() .
.
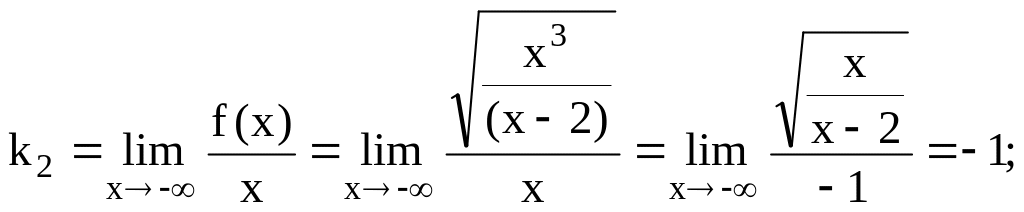
![]() .
.
Итак, наклонные
асимптоты:
![]() ,
т.е.
,
т.е.
![]() .
.
Осн. лит. 14, часть 1, [202-214]
Доп. лит. 29, [277-279].
Контрольные вопросы:
1. Как используется
правило Лопиталя для устранения
неопределенностей вида
![]() ,
,
![]() и
и![]() ?
?
2. Как определяются интервалы монотонности и выпуклости графика функции?
3. Чему равен угловой коэффициент наклонной асимптоты?
Практическое занятие № 10. Неопределенный интеграл. Свойства неопределенного интеграла. Таблица основных интегралов. Метод подстановки. Интегрирование по частям.
Задания: А3 – 8.1 [14], часть 1, № 1-8, А3 – 8.2 [14], часть 1, № 1-8, А3 – 8.4 [14], часть 1, № 1-4. А3 – 8.5 [14], часть 1, № 1-3.
Методические
рекомендации.
При нахождении неопределенных
интегралов используются их свойства и
таблица интегралов. Для приведения
заданного интеграла к табличному
применяется методы подведения под знак
дифференциала и метод подстановки. При
использовании метода интегрирования
по частям нужно правильно представить
подынтегральное выражение в виде
произведения двух сомножителей
![]() и
и![]() .
.
Пример 1.
Вычислить интеграл
![]() .
.
Решение. Представляя интеграл алгебраической суммы в виде суммы интегралов, вынося постоянные множители за знаки интегралов и применяя формулы 1,2 таблицы основных интегралов, получим
![]() Здесь и далее
произвольные постоянные, входящие в
каждый из складываемых неопределенных
интегралов, объединяются в одну
произвольную постоянную.
Здесь и далее
произвольные постоянные, входящие в
каждый из складываемых неопределенных
интегралов, объединяются в одну
произвольную постоянную.
Пример 2. Найти
интеграл
![]() .
.
Решение. Полагаем
![]() ,
внесем функцию
,
внесем функцию
![]() под знак дифференциала, получим:
под знак дифференциала, получим:
![]() .
.
Пример 3. Найти
интеграл
![]() .
.
Решение. Полагаем
![]() ,
,
![]() ,
тогда
,
тогда
![]() .
.
Тогда
![]() .
.
Полагаем
![]() ,
так как достаточно иметь какую – либо
одну первообразную. Итак,
,
так как достаточно иметь какую – либо
одну первообразную. Итак,
![]() .
.
Применяя формулу
интегрирования по частям, получим:
![]()
![]() .
.
Осн. лит.: 14 , часть 2, [15-34]
Доп. лит. : 29, [297-301].
Контрольные вопросы:
1. Как правильно
представить подынтегральное выражение
в виде произведения двух сомножителей
и
,
если подынтегральная функция имеет
![]() ?
?
2. Как внести множитель под знак дифференциала?
3. Как выделить целую часть у неправильной дроби подынтегральной функции?
Практическое занятие № 11. Методы интегрирование некоторых классов функции.
Задания: А3 – 8.6 [14], часть2, № 1-5, А3 – 8.7 [14], часть2, № 1-4, А3 – 8.8 [14], часть2,
№ 1-5.
Методические рекомендации. При интегрировании дробно-рациональную функцию можно представить в виде суммы многочлена и простейших дробей. При разложении дроби на простейшие дроби удобно использовать метод неопределенных коэффициентов. Для избавления от иррациональностей нужно выбрать правильную подстановку, которая позволит привести заданный интеграл к табличному.
Пример 1. Найти
интеграл
![]() .
.
Решение. Выделим полный квадрат из трехчлена:
![]()
![]() .
.
Тогда![]() .
.
Примет 2. Найти
интеграл
![]() .
.
Решение. Подынтегральная функция – неправильная рациональная дробь, поэтому выделим ее целую часть делением числителя на знаменатель
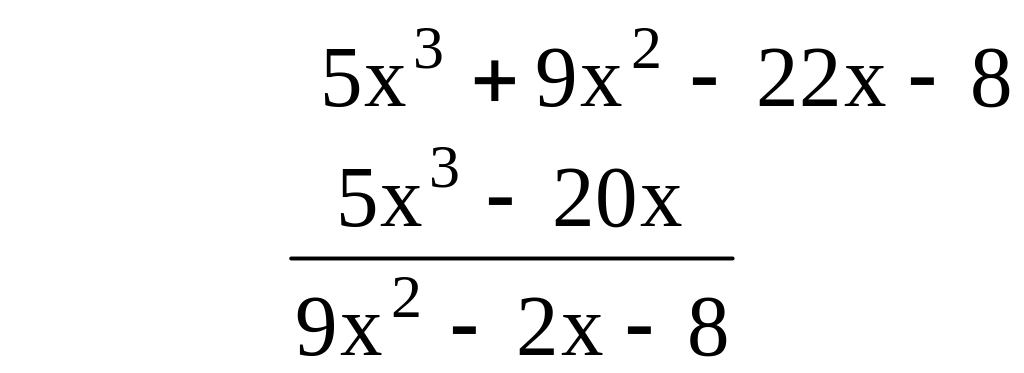

![]() .
.
Следовательно,
![]() .
.
Полученную справа
правильную дробь разложим на простые
дроби и учитывая, что
![]() ,
получим
,
получим
![]() .
.
Приводя правую часть к общему знаменателю и приравнивая числители, получим равенство:
![]()
Коэффициенты при одинаковых степенях в обеих частях равенства должны быть равны. Тогда
![]()
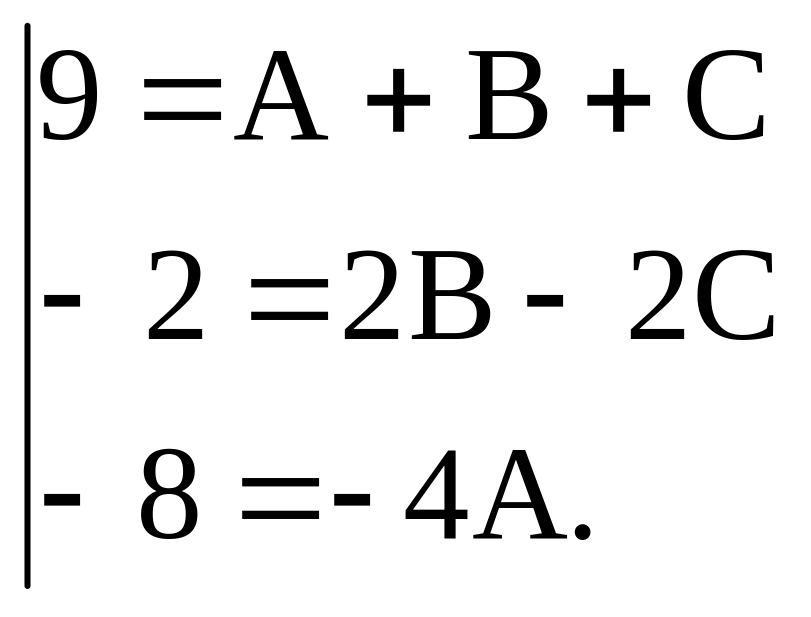 ,
,
откуда
![]()
![]() .
.
Итак,
![]()
![]() .
.
Пример 3. Найти
интеграл
![]() .
.
Решение. Выпишем
показатели
![]() :
:
![]() .
Общий знаменатель этих дробей равен 6,
поэтому полагаем
.
Общий знаменатель этих дробей равен 6,
поэтому полагаем
![]() ,
отсюда
,
отсюда
![]() .
Тогда
.
Тогда
![]()
![]()
![]()
![]() .
.
Пример 4. Найти
интеграл
![]() .
.
Решение. Применяя универсальную подстановку , получим

![]()
 .
.
Осн. лит. 14, часть 2, [35-48].
Доп. лит.: 29, [297-304].
Контрольные вопросы:
1. Какие тригонометрические подстановки применяются для интегрирования иррациональных функции?
2. Какая подстановка является универсальной для интегрирования тригонометрических функции?
3. Как вычислить наименьшее общее кратное (НОК) знаменателей дробей, для приведения интеграла от иррациональной функции к рациональной?
Практические занятия № 12-13. Определенный интеграл, его приложения.
Задания: А3 – 9.1 [14], часть 2, № 1-8, А3 – 9.2 [14], часть 2, № 6-10, А3 – 9.3 [14], часть 2, № 1-4, А3 – 9.4 [14], часть 2, № 4-6.
Методические рекомендации. При вычислении определенного интеграла с известной первообразной нужно использовать формулу Ньютона-Лейбница. Приложение определенного интеграла имеет широкое применение в различных разделах математики и механики. Например, формула вычисления площади криволинейной трапеции зависит от вида задания подынтегральной функции. Вычисление несобственных интегралов основано на его определении.
Пример 1.
Вычислить интеграл
![]() .
.
Решение.
Положим
![]() .
Если
меняется от 0 до 1, то переменная
.
Если
меняется от 0 до 1, то переменная
![]() меняется от 0 до
меняется от 0 до
![]() .
На отрезке
.
На отрезке
![]() функция
функция
![]() монотонна, непрерывна и имеет непрерывную
производную. Применяя правило замены
переменной в определенном интеграле,
получим
монотонна, непрерывна и имеет непрерывную
производную. Применяя правило замены
переменной в определенном интеграле,
получим
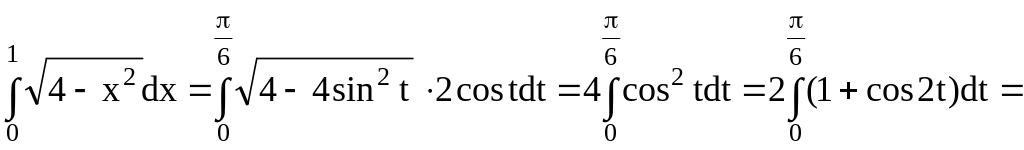
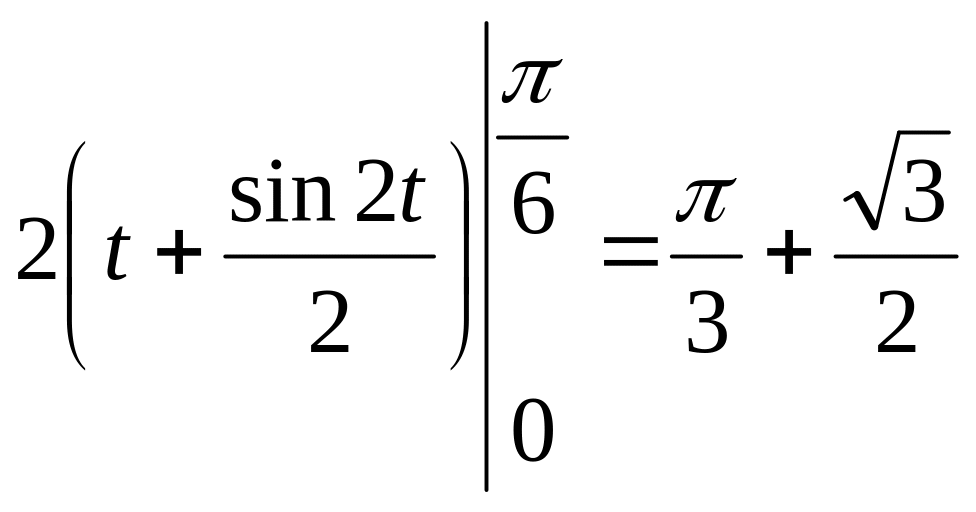 .
.
Пример 2. Найти площадь фигуры, ограниченную первой аркой циклоиды
![]() и
отрезком оси абсцисс.
и
отрезком оси абсцисс.
Решение. Начертим данную кривую
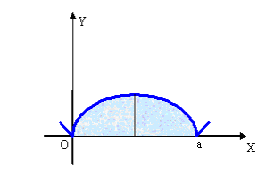
Рис.2
Точки
и
![]() соответствуют значениям параметра
соответствуют значениям параметра
![]() и
и
![]() .
Вычислим площадь фигуры:
.
Вычислим площадь фигуры:
![]()
![]() (кв.ед.)
(кв.ед.)
Осн. лит.: 14, часть 2, [150-173]
Доп. лит.: 29, [305-310], [312-314].
Контрольные вопросы:
1. Как вычислить площадь с помощью определенного интеграла?
2. Как вычислить длину дуги кривой?
3.Вычисление объема тела вращения?
Практическое занятие № 14. Дифференциальные уравнения первого порядка
Задания. АЗ-11.1 [14] часть 2, №№1-7, АЗ-11.2 [14], №№1-7.
Методические
рекомендации.
При нахождении решения линейного
уравнения
![]() ,
можно пользоваться формулой
,
можно пользоваться формулой
![]()
Пример 1. Решить
уравнения с разделяющимися переменными
1)
![]() .
Разделяем переменные
.
Разделяем переменные
![]() ;
;
![]() ;
;
![]() ;
;![]() ;
;
![]()
2)
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Пример 2 .
![]() .
Справа стоит однородная функция нулевого
измерения, следовательно, это однородное
уравнение. Делаем замену
.
Справа стоит однородная функция нулевого
измерения, следовательно, это однородное
уравнение. Делаем замену
![]() .
Тогда
.
Тогда
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Разделяя
переменные, получим
![]() ;
;
![]() .
.
Отсюда, интегрируя находим
![]() ;
;
![]() ;
;
![]() .
.
Подставляя
![]() ,
получим общий интеграл исходного
уравнения
,
получим общий интеграл исходного
уравнения
![]() .
.
Пример
3.
![]() .
.
Переходить
к виду, разрешенному относительно
производной, не обязательно.
,
![]() ,
,
![]() .
Подставляем эти значения в уравнение.
.
Подставляем эти значения в уравнение.
![]() ,
,
![]() .
Разделяя переменные, получим
.
Разделяя переменные, получим
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Подставляя вместо
.
Подставляя вместо
![]() ,
получим
,
получим
![]() ,
,
![]() ,
,
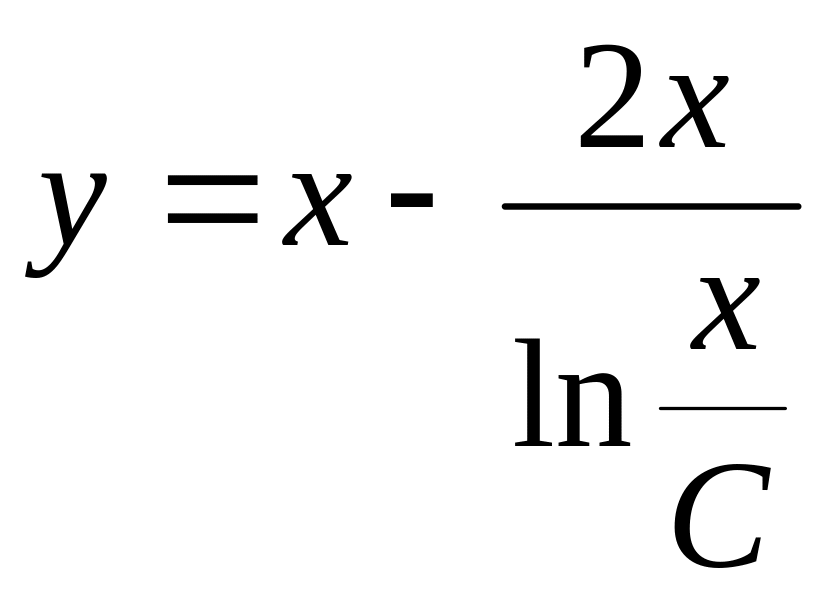 -
общее решение.
-
общее решение.
Пример
4. Решить
уравнение
![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;![]() ;
;![]() ;
;
![]() ;
;![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Осн. лит. 14, часть 2, [243-259]
Доп. лит. 29, [315-320], [321-330].
Контрольные вопросы:
1. Общее решение дифференциального уравнения
2. Дифференциальные уравнения с разделяющимися переменными
3. Линейные дифференциальные уравнения первого порядка
Практическое занятие №15. Дифференциальные уравнения высших порядков, допускающие понижение порядка
Задания. АЗ-2.2 [14] часть 1, №№1-7, АЗ-2.3 [14], №№1-7.
Методические рекомендации. При нахождении решения линейного уравнения высших порядков, допускающие понижение порядка надо знать их типы:
1.Общее решение уравнения вида находим методом n-кратного интегрирования. После n-кратного интегрирования получаем общее решение уравнения.
2.Пусть дифференциальное уравнение n-го порядка не содержит искомой функции и ее производных до (к-1) –го порядка включительно. Вводим новую известную функцию z(x) по формуле z=y(k) .
3.Дифференциальное уравнение n-го порядка, не содержащее явно аргумент x . В этом случае порядок уравнения всегда можно понизить на единицу, введя новую функцию p(y)=y\
Пример
1.
Найти общее решение уравнения
![]() .
.
Согласно формуле и правилам интегрирования, имеем
![]() .
.
Далее в соответствии с решением находим
![]()
Проинтегрировав последнее равенство еще два раза, получим общее уравнение исходного уравнения
![]() ,
,
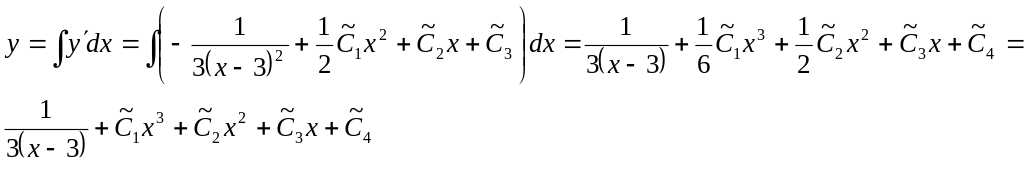
Осн. лит. 14, часть 2, [259-264]
Доп. лит. 29, [330-342], [344-350].
Контрольные вопросы:
1. Типы уравнений высших порядков, допускающие понижение порядка.
2. Дифференциальные уравнения высших порядков, допускающие понижение порядка
2.4 Планы занятий в рамках самостоятельной работы студентов (СРСП)
№ |
Задания |
Форма проведения |
Методические рекомендации |
Рекомен. литература |
1 |
Вычисление определителей высших порядков. Вычисления ранга матрицы.
|
Тренинг |
Необходимо понизить порядок определителя обнуляя элементы строки или столбца. При вычислении ранга можно применить метод нулей и единиц. |
осн.: 15, [.40-43], доп.:29, [182-188] |
2 |
Системы линейных однородных алгебраических уравнений |
Тренинг. Контроль |
Рассмотреть
случай когда ранг матрицы системы
меньше числа неизвестных (т.е. |
осн.:15, [44-46], доп.:29, [189-192] |
3 |
Линейные операции над векторами. Проекции вектора на ось. |
Тренинг |
Использование правил треугольника и параллело-грамма. Использование определение проекции. |
осн.:15, [48-50], доп.:30, [41-109] |
4 |
Приложение скалярного, векторного и смешанного произведения векторов. |
Тренинг Контроль |
Вычисление равнодейст-вующей и вращающего момента силы. Вычисление объемов фигур. |
осн.:15, [51-55], доп.:30, [110-142] |
5 |
Решение геометрических задач алгебраическими методами. |
Тренинг
|
Определение составляю-щих геометрических фигур на плоскости. |
осн.:15, [15-25], доп.:29, [37-239] |
6 |
Взаимное расположение прямых и плоскостей в пространстве. |
Тренинг Контроль |
Рассматривается взаимное расположение между направляющими векторами прямых и нормальными векторами плоскостей. |
осн.:15, [57-65], доп.:29, [244-247].
|
7 |
Построение кривых и поверхностей второго порядка. |
Тренинг |
Параметры входящие в канонические уравнения позволяют построить кривые и поверхности второго порядка. |
осн.:15, [26-30], [68-73], доп.: 29, [239-243], [247-251]. |
8 |
Сложная, обратная и неявная функция. |
Устный опрос. Тренинг |
По виду аналитического задания функции определить свойства. |
осн.: 15, [150-154], доп.:29, [255-261] . |
9 |
Применение теорем о пределах. Исследование функции на непрерывность. |
Консультация Тренинг |
Использовать методы вычисления пределов. Применять определения односторонних пределов |
oсн.: 15, [155-164], доп.:29, [261-267]. |
10 |
Вычисление производной неявной функции. Метод логарифмического дифференцирования. |
Тренинг. Контроль |
Метод основан на последо-вательном применении ло-гарифмирования и диффе-ренцирования функции. |
осн.:15, [165-174], доп.:29, [272-275] |
11 |
Вычисление пределов с применением правило Лопиталя. Разложение многочлена по формуле Тейлора. |
Консуль-тация Тренинг |
Рассмотреть устранение не-определенностей путем многократного дифферен-цирования функции. |
осн.:15, [181-188], доп.:29, [264-277]. |
12 |
Построение графиков функции по характерным точкам. |
Тренинг. Контроль |
Целесообразно выполнение операций исследования сопровождать постепенным построением графика функции. |
осн.:15, [196-197], доп.:29, [277-279].
|
13 |
Интегрирование простейших рациональных дробей. |
Консультация. Тренинг |
При вычислении
интегралов вида
|
oсн.:15, [235-240], доп.:29, [297-301].
|
14 |
Интегрирование иррациональных выражений с помощью тригонометрических подстановок |
Тренинг |
Интегралы |
oсн.:15, [246-259], доп.:29, [297-305] |
15 |
Системы дифференциальных уравнений. |
Тренинг. Контроль |
Рассмотреть метод инте-грирования системы диф-ференциальных уравнений с постоянными коэффи-циентами с помощью матриц (видоизмененный метод Эйлера) |
осн.:15, [.264-268] доп.:29, [305-310].
|
