Векторы и линейные операции над ними. Скалярное и векторное произведения. Смешанное произведение трех векторов.
Векторы используются для описания величин имеющих определённое направление. Примерами таких величин являются сила, скорость, перемещение.
Определение. Вектором называется отрезок с выбранным направлением, или направленный отрезок.
Вектор с началом
в точке A и с концом в точке B
обозначается через
,
кроме того вектор
можно обозначать одним символом, например
.
Вектор, у которого начало совпадает с
его концом
называется нулевым вектором и
обозначается через
.
Длина отрезка, изображающего вектор
,
называется модулем этого вектора
и обозначается |
|.
Векторы
,
параллельные одной прямой называются
коллинеарными. Нулевой вектор
считается коллинеарным любому вектору.
Два вектора
и
считаются равными, если они
равны по модулю, коллинеарны и одинаково
направлены. Из этого определения следует,
что при параллельном переносе вектор
не меняется, по этому в качестве начала
вектора можно выбрать любую точку.
Линейными операциями над векторами называются умножение вектора на число и сложение векторов.
Линейные операции над векторами обладают следующими свойствами.
1
=
0
=
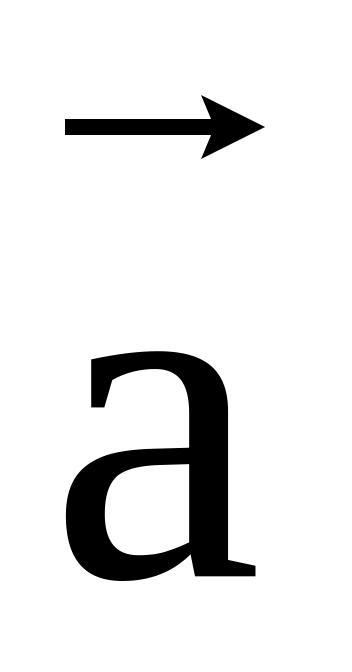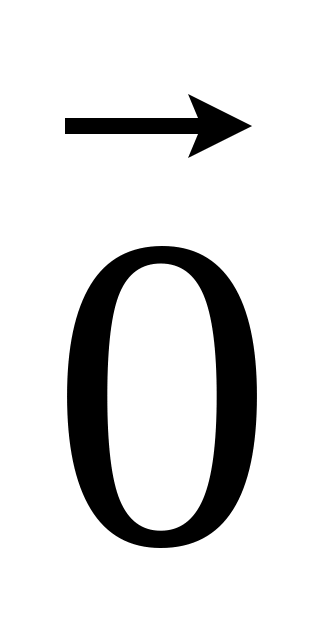
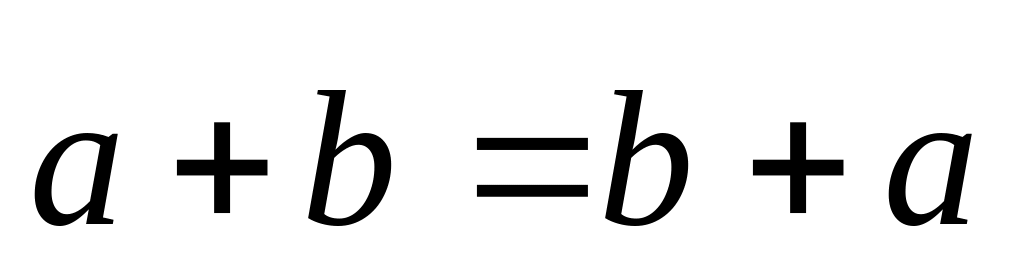
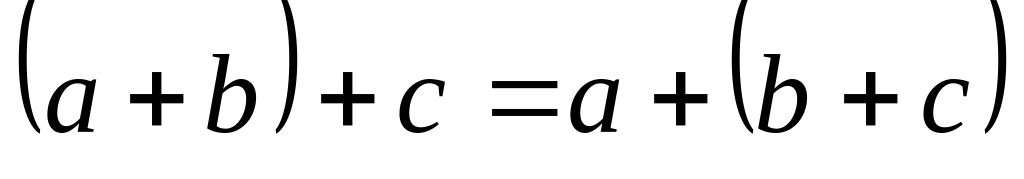
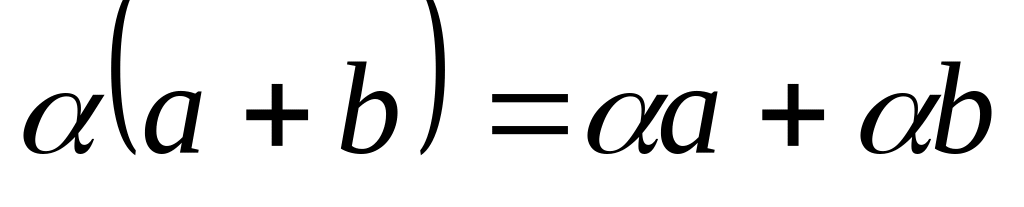
Определение.
Любой ненулевой вектор
на прямой называется базисным
вектором этой прямой.
Любая пара неколлинеарных векторов
плоскости называется базисом
этой плоскости. Любая тройка
некомпланарных векторов
называется базисом пространства.
Теорема. Пусть
в декартовой системе координат Oxyz
заданы две точки A(xA,yA,zA)
и B(xB,yB,zB),
тогда в базисе {
,
,
}
вектор
имеет координаты ((xВ–
xА),(yВ–yА),(zВ–zА)).
Скалярное произведение векторов и его свойства
Имеются три вида произведений векторов: скалярное, векторное и смешанное. Название первого из них произошло от слова скаляр – число. Скалярная величина в математике – это величина, принимающая численные значения.
Определение.
Скалярным произведением векторов
и
называется число, равное произведению
модулей этих векторов на косинус угла
между ними, т. е.
.
Скалярное
произведение обозначается символами
.
Свойства скалярного произведения
10 . Для
любых векторов
и
:
,
т.е. это произведение коммутативно.
20 . Для
любого вектора
:
.
30 . Скалярные
произведение ненулевых векторов
и
равно
только в том случае, когда эти векторы
ортогональны (перпендикулярны).
40 . Для любых векторов и верно соотношение
.
50 . Для
любого вектора
с координатами
в базисе
верно
,
,
.
60 . Постоянный
множитель можно выносить за знак
скалярного произведения, т.е. для любых
векторов
,
и числа
верно:
.
70 . Cкалярное
произведение обладает свойством
дистрибутивности, т.е. для любых векторов
:
.
Векторное произведение векторов и его свойства
Это произведение
определено только для пространственных
векторов
и
,
и оно обозначается символами
или
Определение.
Векторным произведением
векторов
и
называется вектор
,
удовлетворяющий трём условиям:
а) Модуль вектора
равен произведению модулей векторов
и
на синус угла между ними:
sin
в)
перпендикулярен
векторам
и
т.е. он перпендикулярен плоскости,
проходящей через вектора
и
.
с)
Тройка
векторов
правая
(см. рис. 2.18).
Отметим следующие свойства векторного произведения.
В отличие от
скалярного произведения
векторное произведение антикоммутативно
т.е. для любых векторов
и
верно:
.
.
Ненулевые
векторы
коллинеарны только в том случае
когда
.
.
Постоянный
множитель можно выносить за знак
векторного произведения
т.е. для любых векторов
и числа
верно:
.
.
Векторное
произведение обладает свойством
дистрибутивности
т.е. для любых векторов
верно
.
Теорема.
Пусть в базисе
векторы
имеют координаты
и
соответственно.
Тогда
в этом базисе
Cмешанное произведение векторов и его свойства
Определение.
Смешанным
произведением
трех векторов
называется число, равное скалярному
произведению векторного произведения
векторов
с вектором
.
Оно
обозначается символами
или
:
.
Свойства смешанного произведения.
10
Смешанное произведение векторов
равно
объему параллелепипеда, построенного
на этих векторах:
Здесь знак “+” берется в случае если тройка векторов правая “” если она левая.
20
Векторы
являются компланарными только в том
случае
когда их смешанное произведение равно
0:
30
При перестановке
местами любых двух векторов смешанного
произведения оно меняет свой знак на
противоположный; т.е.
4.
Постоянный
сомножитель можно выносить из любого
сомножителя смешанного произведения
т.е. для любых векторов
и числа
.
5.
Смешанное
произведение дистрибутивно для любого
сомножителя
т.е. для любых векторов
верно:
.
Теорема.
Пусть в базисе
векторы
имеют координаты соответственно
и
,
тогда их смешанное произведение
записывается в виде определителя:
.
Осн. лит.: 1, [34-48], 19, [12-20, 66-72, 83-87]
Доп. лит.: 30, [41-109].
Контрольные вопросы
1.В чем отличие скалярного произведения от векторного произведения векторов? Перечислите основные свойства скалярного и векторного произведений.
2. Что называется смешанным произведением?
3. Укажите условие коллинеарности двух векторов.
Лекция № 4. Аналитическая геометрия.
Плоскость
Пусть плоскость
проходит через три точки
,
и
,
не лежащие на одной прямой. Тогда векторы
и
являются направляющими для плоскости
,
подставив их координаты в уравнение с
направляющими векторами, получим:
.
Это уравнение называется уравнением плоскости, проходящей через три заданные точки.
Теорема. Любая
плоскость
в пространстве
определяется своим общим уравнением
вида
,
где
,
задает некоторую плоскость в пространстве.
Определение.
Вектор
,
перпендикулярный плоскости
,
называется нормальным вектором
этой плоскости.
Теорема о
нормальном векторе плоскости. Вектор
с координатами
является нормальным для плоскости
с уравнением
в пространстве
.
Следствие 1.
Косинус угла
между
плоскостями
и
с нормальными
векторами
и
находится по формуле:
.
Следствие 2. Эти плоскости перпендикулярны только в том случае, когда
.
Следствие 3. Эти плоскости параллельны только в том случае, когда
.
Если же
,
то плоскости
и
совпадают.
Пусть плоскость
проходит через точку
перпендикулярно вектору
.
Возьмем на плоскости произвольную точку
M(x,y,z)
и составим вектор
=
.
При любом расположении точки М на
плоскости вектора
и
взаимно перпендикулярны, поэтому их
скалярное произведение равно нулю.
=0.
Тогда
.
Это уравнение называется уравнением плоскости с нормальным вектором.
Пусть плоскость
не проходит через начало координат и
пересекает оси
в точках с координатами
и
соответственно. Тогда уравнение этой
плоскости имеет вид:
.
Это уравнение называется уравнением плоскости в отрезках
Теорема. Расстояние
от точки
до плоскости
определяется формулой:
.
Осн. лит.: 1, [49-71], 9, [23-33]
Доп. лит.: 29, [199-206]
Контрольные вопросы
1. Условие параллельности плоскостей.
2. Условие перпендикулярности плоскостей.
3. Расстояние от точки до плоскости
Лекция № 5. Прямая в пространстве
Пусть в пространстве
имеется прямая
с направляющим вектором
.
– фиксированная точка этой прямой,
– произвольная точка на
.
Запись векторного уравнения прямой
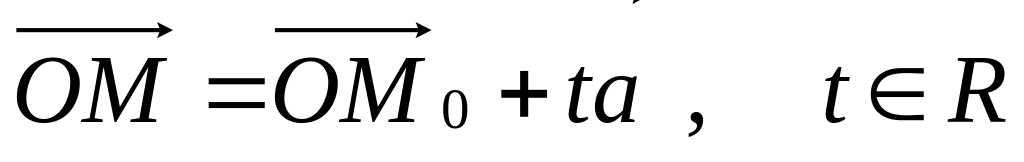
2. Записав три координаты обеих частей векторного уравнения прямой, получим
Эти уравнения называются параметрическими уравнениями прямой в пространстве.
3. Поскольку
векторы
и
коллинеарны, то их координаты
пропорциональны, поэтому
.
Эти уравнения
называются каноническими уравнениями
прямой в пространстве. В
соответствии с количеством знаков
равенства таких уравнений два
и понимать их нужно в смысле пропорций.
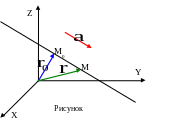
Из-за того, что в знаменателях канонических уравнений могут оказаться нули, предпочтительнее пользоваться параметрическими уравнениями.
Теорема 1.
Косинус угла
между прямыми
и 
находится по формуле
.
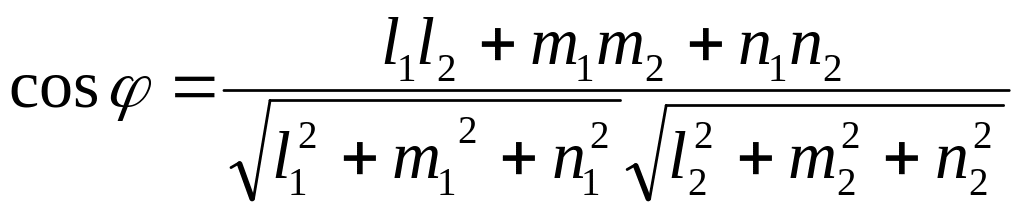Эти прямые перпендикулярны только в том случае, когда
.
Эти прямые параллельны только в том случае, когда
.
Если при выполнении этого условия
,
то
прямые
и
совпадают.
Все утверждения этой теоремы следуют
из соответствующих свойств направляющих
векторов. В последнем случае прямые
и
имеют общую точку.
Теорема 2. Синус угла между плоскостью и прямой
находится по
формуле:
.
Прямая и плоскость
перпендикулярны только в том случае,
когда
.
Прямая параллельна
плоскости только в том случае, когда
.
Если при выполнении
этого условия
,
то прямая
лежит
в плоскости
.
4. Две параллельные плоскости в пересечении определяют прямую в пространстве. Система из двух уравнений этих плоскостей с тремя неизвестными называется общими уравнениями прямой:
.
Осн. лит.: 1, [49-71], 19, [23-33]
Доп. лит.: 30, [151-168].
Контрольные вопросы:
1. Расстояние от точки до прямой.
2. Условие параллельности двух прямых.
3. Угол между плоскостью и прямой
Лекция № 6. Кривые второго порядка на плоскости.
Общее уравнение кривой второго порядка. Поверхности второго порядка
1. Пусть на
плоскости
имеются две точки
и
,
называемые фокусами на расстоянии
друг от друга (
– фокусное расстояние). Для определенности
расположим их на оси
симметрично относительно начало
координат, т.е.
и
.
Пусть 2a>2c
Определение.
Эллипсом называется
геометрическое место точек
плоскости, сумма расстояний, от которых
до двух выбранных фокусов, постоянна и
равна
.
2. В частном
случае, когда фокусное расстояние
эллипса
,
два фокуса эллипса совпадают с его
центром. При этом
и каноническое управление эллипса
принимает вид
или
.
Это уравнение
называется каноническим уравнением
окружности радиуса а. У окружности
эксцентриситет
,
а директрисы отсутствуют.
Уравнение окружности
радиуса а с центром в точке
имеет вид:
.
Определение.
Гиперболой
называется геометрическое место точек
плоскости, разность расстояний от
которых до двух выбранных фокусов
постоянна и равна
.
И каноническим уравнением гиперболы записывается так:
,
где
.
Число
а называется действительной
полуосью
гиперболы,
а число
– ее мнимой
полуосью.
Определение.
Прямая
называется асимптотой
кривой
,
если расстояние от точки на кривой до
этой прямой стремится к нулю при удалении
точки вдоль кривой в бесконечность.
Определение. Параболой называется геометрическое место точек плоскости, расстояние от которых до фокуса совпадает с расстоянием до директрисы.
Определение.
Кривой второго порядка называется
множество точек плоскости, декартовы
координаты которых удовлетворяют
уравнению
.
Здесь хотя бы одно
из чисел
отлично от нуля. Это уравнение называется
общим уравнением кривой второго
порядка.
Если на плоскости
должным образом выбрать систему координат
,
то в этой системе координат уравнение
кривой примет канонический вид одной
из кривых, рассмотренных выше (кроме
нескольких вырожденных случаев).
Теорема. Для
любой кривой второго порядка найдется
декартова система координат
,
в которой уравнение кривой примет один
из следующих видов. (Здесь
).
1)
-
(эллипс);
2)
-
(гипербола);
3)
-
(парабола);
4)
-
(точка
);
5)
или 
(пустые множества);
6)
(пара пересекающихся прямых)
и
.
7)
(пара параллельных прямых
).
8)
(прямая – ось
).
Рассмотрим вначале
частные виды поверхностей, определяемых
в пространстве уравнениями, в которых
неизвестные
присутствуют только в первой или во
второй степени.
1. Пусть в пространстве имеется кривая и прямая .
Определение. Цилиндрической поверхностью (цилиндром) с направляющей и образующей называется геометрическое место точек пространства, лежащих на прямых, проходящих через точки параллельно
Эллиптический цилиндр имеет направляющей эллипс и каноническое уравнение
1.2 Гиперболический цилиндр имеет направляющей гиперболу и каноническое уравнение
1.3. Параболический цилиндр имеет направляющей параболу и каноническое уравнение
1.4. Уравнение
определяет ось
1.5. Уравнения
и
- пустое множество.
1.6. Уравнение
- пара пересекающихся по оси
плоскостей
1.7.
- пара плоскостей, параллельных
.
1.8.
- плоскость
.
Все перечисленные поверхности называются цилиндрическими поверхностями второго порядка.
Пусть в пространстве
имеется кривая
и точка
,
не лежащая на
.
Определение. Конической поверхностью (конусом) с направляющей и вершиной называется геометрическое место точек пространства, лежащих на прямых, проходящих через и пересекающих .
2.Поверхность, определяемая каноническими уравнениями
называется
эллипсоидом, а числа
– его полуосями.
3.Поверхность, определяемая каноническим уравнением
(a,
b, c>0),
называется двуполостным гиперболоидом.
4.Поверхность,
определяемая каноническим уравнением
,
,
называется однополостным гиперболоидом..
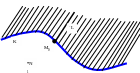
Поверхность, имеющую форму однополостного гиперболоида можно целиком составить из прямых линий. Строительные конструкции такой формы обладают большой прочностью при относительной простоте изготовления. Так первая телебашня в г. Москве составлена из кусков гиперболоидов, каждый из которых построен из прямолинейных металлических форм (см. рисунок).
5. Поверхность,
определяемая каноническим уравнением
,
называется эллиптическим параболоидом.
6. Поверхность, определяемая каноническим уравнением
,
называется гиперболическим параболоидом.
Так же, как и однополостный гиперболоид, с помощью конструкций в виде гиперболического параболоида, составленных из прямолинейных балок осуществляют строительство перекрытий больших размеров, например, крыш над стадионами.
7. Определение. Поверхностью второго порядка называется множество точек пространства, декартовы координаты которых удовлетворяют уравнению
Здесь
хотя бы один коэффициент
должен быть отличен от нуля.
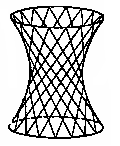
Рисунок
Заметим, что все рассмотренные выше поверхности подходят под это определение. Оказывается, что этими поверхностями и исчерпываются поверхности второго порядка.
Теорема. Любая поверхность второго порядка в пространстве является одной из следующих поверхностей:
одной из цилиндрических поверхностей второго порядка;.
конусом второго порядка
Эллисоидом
одно – или двуполостным гиперболоидом;
эллиптическим или гиперболическим параболоидом.
Найдется,
такая декартова система координат
,
в которой уравнение поверхности принимает
канонический вид.
Осн. лит.: 1, [135-172] , [121-138], 19, [52-58]
Доп. лит.: 29, [206-209], 30, [143-204].
Контрольные вопросы:
1. Определение эллипса как геометрического места точек.
2. Определение уравнение параболы, гиперболы
3.Общее уравнение поверхности второго порядка
4. Какая поверхность называется цилиндрической?
5. Из какой поверхности составлено 1-ая телебашня в г. Москве?
Лекция № 7. Введение в анализ. Функция. Предел и непрерывность
Определение.
Функцией f
с областью определения D и областью
значений Е называется некоторое
отображение из D в Е, т. е.
соответствие, при котором каждому
элементу
сопоставляется единственный элемент
.
Способы задания.
а) Табличный. Функция может быть задана в виде таблицы.
б) Графический.
Графиком функции
называется
множество точек (х,у) плоскости
таких, что
и
.
График даёт наглядное представление о
характере поведения функции.
в) Аналитический. Аналитическим способом, т. е. с помощью одной формулы можно задавать только элементарные функции. Это самый универсальный способ задания функции, из которого можно получить и таблицу и график.
Элементы поведения функции
Ограниченные
величины и функции. Переменная
величина
называется
ограниченной, если существует такое
число
,
что все значения
попадают
в интервал
.
Иными словами, для всех значений
выполняется
неравенство
Для функции
ограниченность означает выполнение
неравенства
при всех
из
области определения.
Возрастание и
убывание функций на интервале. Функция
называется возрастающей на некотором
интервале, если для любых двух значений
аргумента, взятых на этом интервале,
большему значению аргумента соответствует
большее значение функции.
Функция называется убывающей на некотором интервале, если для любых двух значений аргумента, взятых на этом интервале, большему значению аргумента соответствует меньшее значение функции
Четные и нечетные
функции. Пусть задана функция
с
областью определения
.
Функция
называется четной, если выполняется
условие
,
функция
называется нечетной, если
Определение.
Число А называется пределом функции
при
,
если для каждого
найдётся такое 0,
что для всех
выполняется неравенство
,
т. е.
.
Свойства функций, имеющих предел.
Предел постоянной функции равен этой постоянной, т. е.
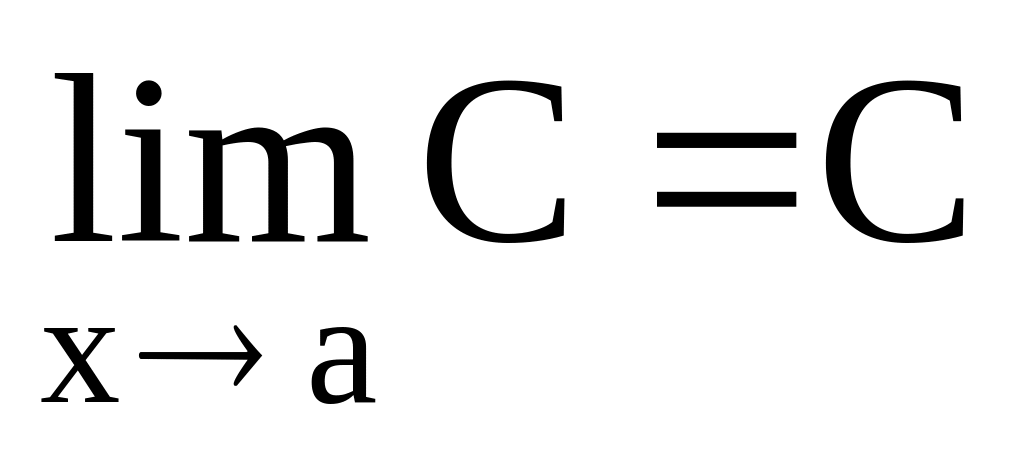.Если предел функции существует, то он единствен.