7.Моделюванні статичного режиму радіоелектронних засобів
Радіоелектронні засоби в своєму складі мають нелінійні компоненти, що при моделюванні статичного режиму або аналізу на великому сигналі потребує використання систем нелінійних рівнянь. Для останніх [2, 5] не існує прямих методів розвязування і тому використовують лише ітераційні методи. В загальному випадку ситема нелінійних рівнянь (рівність нулю n функцій fi від n невідомих xі) має вигляд:
|
(7.1) |
або
F(X)=0.Нижче наведено кілька методів розвязання нелінійних систем рівнянь та їх особливості.
7.1.Метод простої ітерації
Метод простої ітерації це розвиток метода простої ітерації для систем лінійних рівнянь і грунтується на припущенні, що система рівнянь (7.1) може бути приведена до вигляду:
|
(7.2) |
.Алгоритм розвязання системи:
використовуючи початкові наближення xj із рівнянь (7.2) послідовно розраховують нові значення xj* , при цьому в кожному і-му рівнянні всі змінні xj (j<i) заміняють на нові значення xj*, розрахованя по попереднім рівнянням;
значення xj* порівнюють попередніми xj і якщо |xj*- xj| <ε (ε<<1), то розрахунки припиняють.
Хоч метод дозволяє отримати розвязок системи, але має певні недоліки. Якщо початкові значення змінних сильно відрізняються від розвязку системи, то процес може не збігатися.
7.2.Метод Ньютона
Метод Ньютона – найбільш ефективний метод розвязування систем нелінійних рівнянь, що значною мірою обумовлене прискореною сходимістю порівняно з методом простої ітерації. Метод грунтується на відображенні всіх n рівнянь системи (7.1) у вигляді скорочених рядів Тейлора:
де
-
прирощення аргументу; О1…
Оn,
- суми членів більш високих порядків,
ніж перший.
Якщо припустити, що вектор Х знаходиться в області збіжності системи рівнянь (хі невеликі, і=1, 2, …, n) і відкинути члени більш високих порядків, то (7.3) може бути представлена у вигляді:
Значення хі вибирають так, щоб fі компенсувало fі , тобто fі = -fі .
Таким чином, розвязання системи нелінійних рівнянь (7.3) зводиться до пошуку значень хі через розвязок лінійної системи рівнянь JX=-F:
де матриця J перших частинних похідних (матриця Якобі, або якобіан) і вектор –F правої частини розраховуються для поточного наближеного розвязку.
Знайдені значення хі використовуються для корегування початкового наближеного розвязку:
Якщо всі корегуючі прирости стають достатньо малими, то розрахунки припиняють. Хоч метод Ньютона має переваги над іншими ітераційними методами, але і для нього існує проблема збіжності.
Задача
7.1.
Починаючи із значення вектора невідомих
,
методом Ньютона розв’язати систему
нелінійних рівнянь
.
Розв’язок. Матриця похідних і вектор правих частин системи рівнянь:
|
|
/x1 |
/x2 |
|
|
J = |
f1/ |
2 (x1 - x2) + 0.5 |
-2 (x1 - x2) |
; F= |
(x1 - x2)2 + 0.5 x1 - 2 |
f2/ |
-2 (x1 - x2) |
2 (x1 – x2) + 1 |
x2 - (x1 - x2)2 |
Хід розвязання задачі наведено у таблиці:
№ |
Х(k-1) |
J |
F |
X |
|
1 |
0 |
0,5 |
0 |
-2 |
4 |
0 |
0 |
1 |
0 |
0 |
|
2 |
4 |
8,5 |
-8 |
16 |
-1,28 |
0 |
-8 |
9 |
-16 |
0,64 |
|
3 |
2,72 |
4,66 |
-4,16 |
3,6864 |
-0,5469 |
0,64 |
-4,16 |
5,16 |
-3,6864 |
0,2735 |
|
4 |
2,1731 |
3,0192 |
-2,5192 |
0,6731 |
-0,1573 |
0,9135 |
-2,5192 |
3,5192 |
-0,6731 |
0,0787 |
|
5 |
2,0157 |
2,5472 |
-2,0472 |
0,0557 |
-0,0156 |
0,9921 |
-2,0472 |
3,0472 |
-0,0557 |
0,0078 |
|
6 |
2,0002 |
2,5005 |
-2,0005 |
0,0005 |
-0,0002 |
0,9999 |
-2,0005 |
3,0005 |
-0,0005 |
0,0001 |
|
7 |
2 |
2,5000 |
-2,0000 |
0,0000 |
0,0000 |
1 |
-2,0000 |
3,0000 |
0,0000 |
0,0000 |
|
Процес зійшовся за 7 ітерацій до x1 = 2 і x2 = 1. При цьому
f1 = (x1 - x2)2 + 0.5 x1 – 2 = (2 - 1)2 + 0.5 * 2 - 2 = 1 + 1 - 2 = 0; |
f2 = x2 - (x1 - x2)2 = 1- (2 - 1)2 = 1 - 1 = 0, |
що засвідчує правильність розвязання задачі.
Задача 7.2. Методом Ньютона розв’язати систему рівнянь:
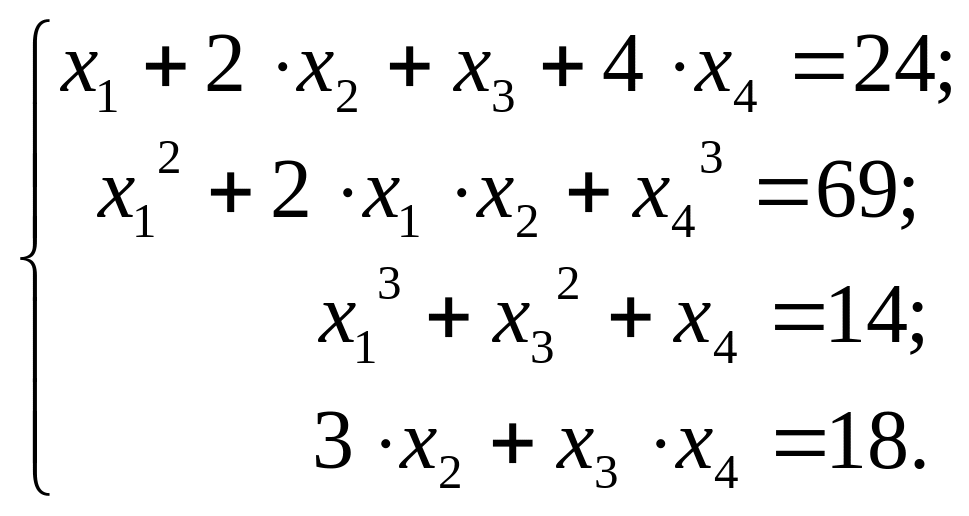
Розв’язок. Перетворена система рівнянь має вигляд:
|
f1 |
|
x1 + 2 x2 + x3 + 4 x4 – 24 |
|
F= |
f2 |
= |
x12 + 2 x1 x2 + x43 – 69 |
. |
f3 |
x13 + x32 + x4 – 14 |
|||
|
f4 |
|
3x2 + x3 x4 – 18 |
|
Матриця похідних і вектор правих частин системи рівнянь (7.5):
|
|
/x1 |
/x2 |
/x3 |
/x4 |
|
|
|
f1/ |
1 |
2 |
1 |
4 |
|
-f1 |
J = |
f2/ |
2 x1+2 x2 |
2 x1 |
0 |
3 x42 |
; -F= |
-f2 |
f3/ |
3 x12 |
0 |
2x3 |
1 |
-f3 |
||
|
f4/ |
0 |
3 |
x4 |
x3 |
|
-f4 |
Фрагмент програми Newton, що реалізує метод Ньютона для сиcтеми рівнянь задачі 7.2 наведений нижче.
Repeat Writeln; write('it=',it:2); for i:=1 to n do write(x[i]:8:3); a[1,1]:=1; a[1,2]:=2; a[1,3]:=1; a[1,4]:=4; a[2,1]:=2*x[1]+2*x[2]; a[2,2]:=2*x[1]; a[2,3]:=0; a[2,4]:=3*x[4]*x[4]; a[3,1]:=3*x[1]*x[1]; a[3,2]:=0; a[3,3]:=2*x[3]; a[3,4]:=1; a[4,1]:=0; a[4,2]:=3; a[4,3]:=x[4]; a[4,4]:=x[3];
dx[1]:=24 -x[1] -2*x[2] -x[3] -4*x[4]; dx[2]:=69 -x[1]*x[1] -2*x[1]*x[2] -x[4]*x[4]*x[4]; dx[3]:=14 -x[1]*x[1]*x[1] -x[3]*x[3] -x[4]; dx[4]:=18 -3*x[2] -x[3]*x[4]; for k:=1 to n-1 do { прямий хід метода Гауса} for i:=k+1 to n do begin z:=a[i,k]/a[k,k]; for j:=1 to n do a[i,j]:=a[i,j]-z*a[k,j]; dx[i]:=dx[i]-z*dx[k]; end; for i:=n downto 1 do {зворотній хід метода Гауса} begin z:=dx[i]; for j:=i+1 to n do z:=z-a[i,j]*dx[j]; dx[i]:=z/a[i,i]; end; kl:=0; write(' dx='); for i:=1 to n do begin if abs(dx[i])> 0.001 then kl:=1; x[i]:=x[i]+dx[i]; write(dx[i]:8:3); end; Until kl=0; |
Результати розвязання системи рівнянь (7.8) для початкового вектора змінних х1 = х2 = х3 = х4 = 1 за допомогою програми Newton наведені в таблиці.
№ |
х1 |
х2 |
х3 |
х4 |
dx1 |
dx2 |
dx3 |
dx4 |
0 |
1.000 |
1.000 |
1.000 |
1.000 |
12.069 |
8.931 |
-12.414 |
-0.379 |
1 |
13.069 |
9.931 |
-11.414 |
0.621 |
-3.692 |
-7.319 |
20.020 |
-0.423 |
2 |
9.377 |
2.612 |
8.606 |
0.198 |
-3.286 |
0.574 |
-1.094 |
0.808 |
3 |
6.091 |
3.186 |
7.512 |
1.006 |
-2.593 |
3.681 |
1.380 |
-1.537 |
4 |
3.498 |
6.867 |
8.892 |
-0.531 |
-1.551 |
6.103 |
-2.722 |
-1.983 |
5 |
1.947 |
12.970 |
6.170 |
-2.514 |
-17.636 |
-93.144 |
9.982 |
48.486 |
… |
… |
… |
… |
… |
… |
… |
… |
… |
13 |
-0.617 |
2.467 |
2.528 |
4.288 |
1.490 |
-0.470 |
0.414 |
-0.241 |
14 |
0.873 |
1.997 |
2.942 |
4.047 |
0.136 |
-0.004 |
0.062 |
-0.047 |
15 |
1.009 |
1.993 |
3.004 |
4.000 |
-0.009 |
0.007 |
-0.004 |
-0.000 |
16 |
1.000 |
2.000 |
3.000 |
4.000 |
-0.000 |
0.000 |
-0.000 |
0.000 |
Процес
з точністю ε=0.001 зійшовся за 16 ітерацій.
Таким чином, вектор невідомих
.