§8. Момент силы и момент импульса относительно точки

и оси. Плечо силы

_r

Пусть в точке «А» приложена сила F , радиус вектор точки «А»,

проведенный из точки «О», равен r (рис.8.1). Момент силы N относи-

тельно точки (в данном случае точки «О»), равен векторному произведению

радиус-вектора r этой точки на вектор силы F , действующей на эту точ-

ку:

= r × F

N=rFsina , (8.1)

29

где a - угол между векторами r и F .

(Точка,

вектор N - это точка, из которой прове-

дён радиус-вектор (на рис.8.1, 8.2 - точка

“O”)).

Проекция момента силы на не-

которую ось (Z) называется моментом

силы относительно этой оси.

Вектор F можно разложить на

две составляющие - параллельную к оси

Z ( F_|| ) и перпендикулярную к ней ( F_^ ,

рис. 8.1):

F = F + F

Вектор F_^ в свою очередь разложим на

_r

составляющие параллельную и перпендикулярную к радиусу R ( F_R ,

_r

F_τ , рис. 8.1) , где R - длина перпендикуляра, проведённого от оси Z к

точке (точка А). Следовательно:

r r r r r r

^ R || R

N =[rF]=[r(F_|| + F_R + F_τ)]=[rF_||]+[rF_R]+[rF_τ]

Обозначим

N_|| = [rF_||] ; N_R = [rF_R] ; N_τ =[rF_τ] (8.3)

_{r r r r}

N = N + N + N

N N N

Из свойств векторного произведения (вектор N перпендику-

лярен каждому из сомножителей) следует, что N_|| и N_R перпендику-

лярны к оси Z (рис. 8.1a,б), поэтому:

N N 0 (8.5)

30

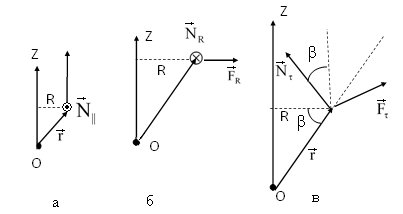
Рис.8.2

Найдём N_τ,Z (рис. 8.2 ,в). Из свойств векторного произведения и рисунка

_r

видно, что угол между N_τ и осью Z (угол b) равен углу между вектором

r и радиусом R. (Углы, стороны которых взаимно перпендикулярны: R

перпендикулярно к Z, r к N_t ). Следовательно:

= × cos β

Из определения векторного произведения:

,

где g- угол между r и F_t . Этот угол равен 90° (рис. 8.1 , 8.2,в).

Поэтому: (8.6)

t , Z

Из рисунка 8.2 в следует:

r cos β = R => N_{t ,Z} = F_τR

Подставим это выражение в

ур-е (8.4) и учтем (8.5):

N_Z=F_tR (8.7)

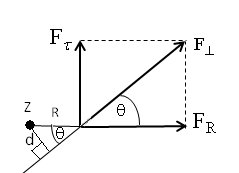
На рисунке 8.3 ось Z

перпендикулярна плоскости

рисунка, d-длинна перпенди-

куляра, опущенного из оси Z

на линию вдоль которой дей-

31

_r

ствует сила F_^ . Величина d называется плечом силы.

d = R sin θ ⇒ N_Z = F_t R = F_t d/ sin θ (8.8)

Из рис. (8.3):

F_τ / sinθ = F_^

Следовательно:

(8.9)

Моментом импульса L относительно точки называется величина, равная:

L = [rp] (8.10)

_r

Момент импульса , относительно оси Z равен проекции вектора L на эту

ось. Повторяя все вышеизложенное (заменив вектор F на вектор P ),

получим:

(8.11)

Смысл обозначений в (8.11) аналогичен тем, что были приняты для мо-

мента силы.

§9. Момент импульса и момент инерции тела

относительно оси. Уравнение моментов. Закон дина-

мики вращательного движения твердого тела

относительно неподвижной оси. Теорема Штейнера

Рассмотрим вращательное движение частицы (материальной точки)

вокруг оси Z (рис. 9.1,ось Z перпендикулярна плоскости рисунка). В

дальнейшем будем рассматривать вращение относительно оси, направ-

ление которой в пространстве не меняется.

Скорость частицы u перпендику-

лярна радиусу вращения R . Следователь-

но, согласно обозначениям §8

u_t=u

Из (8.11) получим:

L_Z=PtR=mu_t=mRu.

Так как u=wR, то

L_z = mR²ω

Рис.9.1

32

I_z = mR²

называется моментом инерции материальной точки относительно оси

вращения. Из (9.1) и (9.2) следует:

L_z = I_zw

В общем случае частица имеет ускорение a_t , создаваемое силой F_t

(рис.9.1). Запишем второй закон Ньютона:

F_τ = ma_τ

Для неменяющегося в пространстве направления оси вращения (т.е. для

рассматриваемого случая )

a_t =bR ⇒F_t=mRb (9.4)

Помножим (9.4) на R:

F_tR=mR²b

Учитывая (8.7) и (9.2), получим

N_Z=I_Zb (9.5)

Уравнение (9.5) обычно называют законом динамики вращательного дви-

жения материальной точки. Так как

β = ⇒

N_z = I_z = (I_zω)

С учетом (9.3) из последнего соотношения находим:

N_z = (9.6)

Рассмотрим твердое тело как систему, состоящую из множества

частиц. Запишем уравнение (9.6) для каждой из них:

dL_{z,i , (9.7)}

N_z,i =

dt

где i - номер частицы. Сложим эти уравнения:

N_z,i = = L_z,i

Обозначим

(9.9)

где N_z момент силы относительно оси, действующий на тело, L_z мо-

мент импульса тела. Следует учесть, что при вычислении N_z моменты

33

внутренних сил сократятся. Поэтому N_z - суммарный

момент внешних сил относительно оси вращения. Таким образом

dL_z

(9.10)

dt

Уравнение (9.10) обычно называют правилом моментов.

Из (9.9) и (9.3) получим:

L_z = L_z,i = I_z,iw , (9.11)

L_Z,i=m_iR_i², (9.12)

Где m_i, R_i - соответственно масс и радиус вращения i-ой точки.

Т.к. угловая скорость всех точек твердого тела одинаковая и равна угло-

вой скорости вращения твердого тела, индекс «i» у w в уравнении (9.11)

не пишется (угловое ускорение b для всех точек тоже одинаковое). Из

(9.11) и (9.12) следует

L_z = w × R_i ² (9.13)

Величина

I_z = I_z,i =

называется моментом инерции тела относительно оси вращения. Видно,

что I_Z зависит от положения оси вращения относительно тела, т.к. от

этого зависит R_i. Следовательно, для различных осей I_Z разное. Для

данной оси I_Z абсолютно твердого тела не зависит от скорости враще-

ния т.к. взаимное расположение частиц такого тела не меняется и , сле-

довательно, R_i от скорости не зависит.

Подставим (914) в (9.13)

L_Z=I_Zw (9.15)

Таким образом, момент импульса тела равен

произведению момента инерции тела на угло-

вую скорость вращения.

Подставим (9.15) в (9.10):

d(I_zω) dω

dt dt

Т.к = β ⇒

N_Z=I_Zb (9.16)

т.е. момент силы действующей на тело, равен

произведению момента инерции тела на его угловое ускорение. Уравне-

34

ние (9.16) обычно называют законом динамики вращательного движе-

ния твердого тела относительно неподвижной оси.

Из изложенного следует, что момент инерции тела надо каждый

раз рассчитывать для той оси, относительно которой тело вращается.

Есть таблицы (в учебниках, пособиях и задачниках) в которых приводят-

ся формулы для расчета I_Z некоторых тел относительно определенных

осей вращения (обычно для осей, проходящих через центр тяжести).

Пусть известен момент инерции I_z,0 относительно некоторой

оси , проходящий через центр тяжести “C” (ось Z₀ на рисунке 9.2). Надо

найти I_z относительно другой оси Z , параллельной оси Z_0. Согласно

теореме Штейнера, I_z равен:

I_Z =I_Z,0+ma² , (9.17)

где m - масса тела , a - расстояние между ося-

ми.

Следует также учесть, что любое тело можно

представить как “сумму” нескольких тел

(например, на рис.9.3 - как два тела). Тогда:

m R^{2 = mi} R^{2 + miRi2 ,}

где первая сумма берется для части 1, вторая - части 2.

Из определения момента инерции, следует:

m_i R_i ^{; Iz,2 =} m_i R_i ^;

где I_Z,1 и I_Z,2 - моменты инерции 1-ой и 2-ой части. Поэтому

I_Z= I_Z,1+ I_Z,2

Аналогичные рассуждения справедливы для “разбиения” абсо-

лютно твердого тела на любое число частей. Следовательно , для тел

сложной формы можно искать моменты инерции каждой из выделенных

“частей “ и затем их сложить .Такое свойство физических величин назы-

вается аддитивностью. Момент инерции тела относительно данной оси

является величиной аддитивной. (Напомним, что масса тела тоже величи-

на аддитивная. Например, для рис.9.3 масса тела m равна

m = m₁ + m₂).

35

Основные формулы поступательного и

вращательного движения.

Поступательное движение Вращательное движение

величина, закон формула величина, закон формула

изменение по-

ложения точи

скорость

поступательно-

го движения

u =

ускорение при

поступательном

движении

масса

сила

z

импульс

Второй закон

Ньютона

dP

dt

* Работа

* Кинетическая

энергия

(* Последние две темы см. § 10)

36